一道直线与椭圆题的解法展示及拓展探究

江苏省海门中学 (226100) 徐巧石

深化能力立意，突出能力与素质的考查始终是高考数学的导向与主题.在考试中构造有一定深度和广度的数学问题时，要注意问题的多样性，体现思维的发散性.2019届高三苏州期初考试中的直线与椭圆一题题干简洁明了，角度小，立意新，有深度，能够激发学生的思维.本文就本人在此题评讲中学生给出不同的解法进行整理评析，最后对该题进行一般性拓展探究.

图1

一、题目

二、解法展示

解法一：由椭圆的对称性可知直线MN的斜率一定存在，设其方程为y=kx+1．设M(x1,y1),N(x2,y2)．

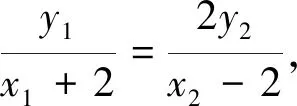
评析：此法是学生容易想到的处理方式利用点在直线上转化，但是需要解一个无理方程.学生如果有信心往下写的话，发现此方程可以因式分解降次处理便迎刃而解.其实这种处理无理方程在江苏高考中一直有所考察，2012年江苏高考试题19题第一问中官方提供的参考答案便是这种处理方法.在高三的复习中要加强对学生运算信心的训练.

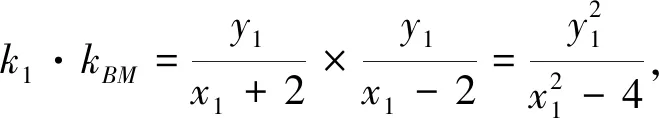
评析：此法观察到点A,B关于原点对称，想到了椭圆中常用的二级结论，将两直线斜率间的倍数关系转化为过同一点两直线斜率间的乘积关系，将不对称结构转化为对称结构，解法一中遇到的问题便可化解.在高三的复习中一些常见的结构需要给学生搭建起命题网络.

评析：此法将对称运用到了极致，完全不需要复杂的运算，便可得到答案，十分巧妙.看似没有用到直线与椭圆联立，实际上在得到kAN=2kBM已经利用M,N在椭圆上，又两次运用M,N在直线y=kx+1上，将直线与椭圆相交隐藏对称的结构中.

转化与化归思想一直是高中数学的重点考察的思想方法，对于题干的等价表述也体现了学生的转化能力，若学生能够对题干从不同的角度重新构图，有可能得到其它的方法.例如：

等价表述1：如图1，过点A作斜率为k1直线AM与椭圆E交于M点，过点B作斜率为k2的直线与椭圆E交于N点，若k1=2k2，且M,N,C(0,1)三点共线，求直线MN的斜率k(k>1).

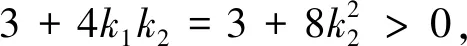
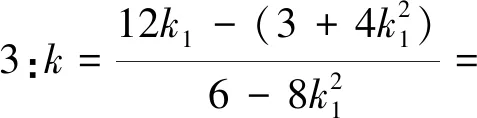
评析：此法通过转化M,N产生的方式，利用M,N,C三点共线得到直线MN的方程.处理1,2利用k=kCN=kCM=kMN整体代换求出斜率k；处理3对于处理的问题要有目标意识，利用分式的合比定理整体取得，技巧性较高，对于数据的处理有较高的要求.

新的数学课程标准提出了数学学科的六大核心素养，其中逻辑推理是得到数学结论、构建数学体系的重要方式.若该问题中去掉三点共线，由k1=2k2能确定直线MN的斜率吗？为什么加上一个C点后就可以确定直线MN？k1=2k2这一条件确定了直线MN的什么量？经过这几个追问可以推知直线MN过定点.由对称性可知定点应在x轴上.所以题目可以先分解为:

如图1，过点A作斜率为k1直线AM与椭圆E交于M点，过点B作斜率为k2的直线与椭圆E交于N点，若k1=2k2，证明直线MN过定点.

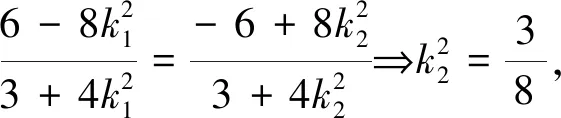
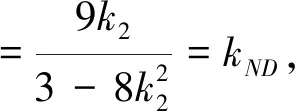
评析：此法通过逻辑推理推得直线MN过定点，进一步揭示了本题的命题背景.实际上此题背景是2010年江苏高考试题的一个结论.

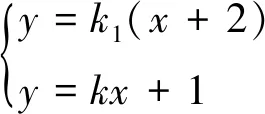
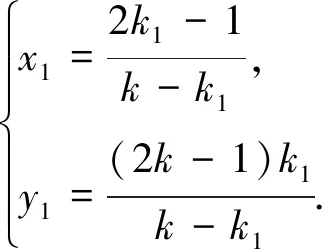
评析：此法通过直线与直线的交点在椭圆上，得到k的值.此种表述方式在2016年江苏高考17题中得以体现.实际上题干的三种不同表述是从三个不同的角度产生点M,N.在平常的教学过程中要让学生能够从不同的角度看待问题，新的角度可能产生意想不到的收获.当然，学过竞赛的学生还想到运用了二次曲线系去解决上述问题，由于二次曲线系不在高考的考查范围，所以不再做详细的解答.

三、拓展探究

将上述解法三一般化可得如下命题：

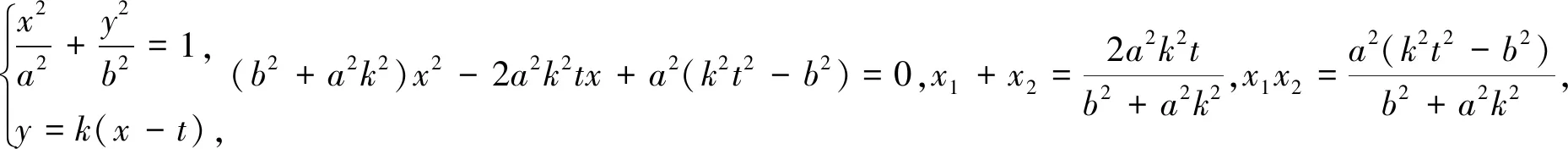
该命题的逆命题也成立：

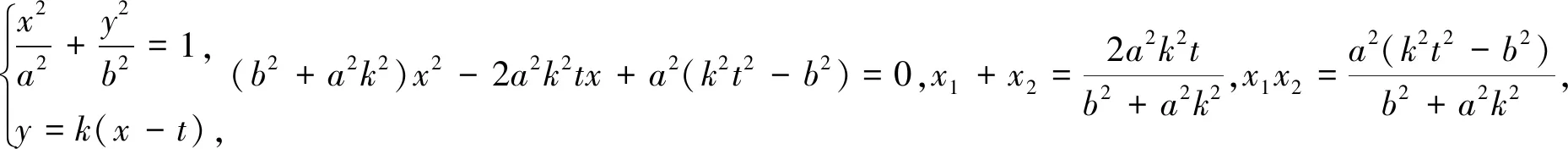
由解法四将原题一般化可得：

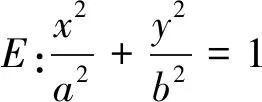
由解法六可得：

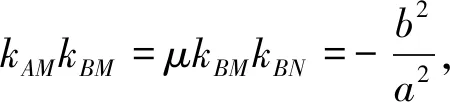
由解法六中联想到2010年江苏省高考题可得：

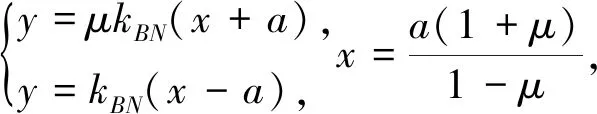
命题4的逆命题也成立，因将命题3中的条件kAM=μkBN(μ>0)进行等价转化可得：

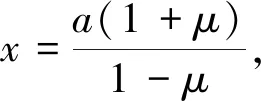
上述命题中若将长轴顶点A,B改为短轴顶点，同样有相应的结论；若将椭圆改为双曲线类比亦可得相应的结论，限于篇幅，不在一一赘述.