关于二次曲线三点共线的统一证明及思考 *

安康学院数学与统计学院 (725000) 赵临龙 延安大学数学与计算机学院 (716000) 王 茜 刘彦灵

文[1]借助《几何画板》，分别对抛物线、椭圆、双曲线给出相关结论，现将这些结论统一为命题1.

命题1 设圆锥曲线E的一个焦点为F，相对应的准线为l，过焦点F的直线交圆锥曲线E于A，B两点，C是圆锥曲线E上的任一点，直线CA，CB分别与准线l交于M，N两点，则以线段MN为直径的圆必过焦点F．

文[2]在文[1]基础上，也通过《几何画板》，分别对抛物线、椭圆、双曲线给出相关结论.

命题2 设抛物线E:x2=-2py(p>0)的焦点为F，相对应的准线为l，过焦点F的直线交抛物线E于A，B两点，点C是抛物线E上的任一点，直线CA，CB分别与准线l交于M，N两点，若FC交抛物线与于D，则D、A、N三点共线，D、B、M三点共线．

我们完全可将命题2-4，统一为命题5，并统一给出证明.

命题5 设二次曲线E的一个焦点为F，相对应的准线为l，过焦点F的直线交二次曲线E于A，B两点，点C是二次曲线E上的任一点，直线CA，CB分别与准线l交于M，N两点，若FC交二次曲线与于D，则D、A、N三点共线，D、B、M三点共线．

1.知识准备

引理[4]如图1,完全四边形ABCD的两对角线AB、CD分别交对角线MN于E、G，则四点A、B、F、E，四点D、C、F、G，四点N、M、G、E均调和分割.

图1 图2

定义2[5]过点P(x0，y0)引二次曲线Γ：ax2+2bxy+cy2+2dx+2ey+f=0的直线PAB交Γ于A、B两点，若该直线上的4点A、B、P、Q满足调和分割，则点Q(x，y)轨迹为点P关于Γ的极线l：ax0x+b(y0x+x0y)+cy0y+d(x0+x)+e(y0+y)+f=0，点P称为Γ的极点.

极线作图已知二次曲线Γ内一点F，作出Γ的极线l.

作法:如图2.过点F作Γ的两直线FAB、FCD，连接直线AC与BD交于点M，连接直线AD与CB交于点N，连接MN即得极点F的极线l.

证明：如图2，设完全四边形ABCD的对角线AB、CD分别交MN于E、G，则四点A、B、F、E和四点D、C、F、G调和分割，即直线EG(MN)为点F关于二次曲线的极线.

2.命题证明

图3

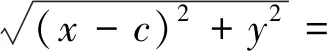
e|x-xQ|⟺(x-c)2+y2=e2(x-xQ)2,即(1-e2)x2+y2-2(c-e2xQ)x+c2-e2x2=0.

在图2中，不妨设直线CA和CB交于点M1，根据极线作图方法，知道M1必在极线(准线l)上，而直线AC与准线l的交点为M，即直线CA和CB交于极线l于点M，于是三点D、B、M共线，同理三点D、A、N共线．

3.解题反思

我们看到，射影几何在揭示几何内部结构方面，有着特殊的作用.但在实际中，射影几何并没有引起人们的高度重视.2011年11月17-18日，应邀参加华中师范大学出版社召开的“高等院校数学教学改革与教材建设研讨会”，会议讨论决定出版具有师范特色的相关课程教材，笔者提出可将反映师范特色的重要课程《高等几何》列为出版计划，得到与会教师的赞成.后在《高等几何》教材编写讨论会上，相关参加编写学校介绍《高等几何》课程开设情况，包括华中师范大学、湖北第二师范学院、湖北工程学院、黄冈师范学院等在内的学校都是将《高等几何》作为选修课，唯独安康学院将《高等几何》作为师范专业的特色课程，这无不反映《高等几何》在师范院校的地位，使许多师范生没有学习高等几何，或学习高等几何下的功夫不够，使高等几何没有成为研究初等几何的重要工具.为此，笔者建议：

(1)师范院校尽可能将《高等几何》作为必修课.正是《高等几何》课程在师范院校的不良地位，致使很多学生未能很好学习它或根本就没有学习.为此，我们经常看到，利用现代信息技术—几何画板探讨几何“新发现”的文章，然后利用初等的解析几何，通过非常复杂的运算，给出问题的结果，不仅浪费了宝贵的时间，而且是在重复前人的研究“成果”.因而，我们呼吁师范院校应该将《高等几何》纳入必修课，使师范生建立射影几何的概念，形成“教师一桶水，学生一碗水”的几何高观点，真正利用高等几何研究初等几何，给出具有研究价值的成果.

(2)将高等几何重要的理论方法向中学数学渗透.要解决初等几何中重复研究的现状，可以有意识将高等几何中能被中学生接受的重要的理论和方法，渗透到中学数学中，使很多教师和学生学习和研究它，不断提升几何的知识结构和应用能力.其实，高等几何问题已不断出现在高考题中，如安徽省的高考题:

(Ⅰ)求椭圆C方程；

(Ⅰ)如果点Q的坐标是(4,4)，求此时椭圆C的方程；

(Ⅱ)证明：直线PQ与椭圆C只有一个交点.

题1直接就是高等几何极点与极线概念的反映；题2也是高等几何极点与极线概念的应用，可参见文[5-6].因此，随着这些知识的研究和普及，高等几何的基本知识将不断被人们认识和接受，逐步形成利用高等几何观点研究初等几何的良好意识和习惯，真正给出有研究意义的“新成果”.