聚焦核心素养 明晰备考方向

潘敬贞 骆妃景 唐明超

摘要：不等式选讲试题是高考二选一的选做题型，是对高中不等式内容的补充和拓展，本文对近七年（2013-2019）高考全国卷不等式选讲试题进行研究，探索其命题规律和特点，并提出备考建议.

关键词：不等式;选做题;复习备考;教学启示

作者简介：潘敬贞（1984-），男，广东汕头人，本科，中学一级教师，研究方向：高中数学教育教学研究;

骆妃景（1987-），男，广东东莞人，硕士，中学一级教师，研究方向：高中数学教育教学研究;

唐明超（1992-），男，云南宜威人，硕士，中学二级教师，研究方向：数学教育研究.1引言

高三数学复习教学不仅肩负着回顾复习知识、理解数学概念的本质，梳理考点、明晰考向，帮助学生构建知识体系，使知识网络化、系统化的任务，还要肩负着引导学生对数学思想方法内涵的理解，提升理性思维能力，发展数学核心素养水平等重任.可谓内容繁多，任务艰巨.尤其是在当前以核心素养为热潮的新课改中，如何做好高三数学复习教学，以达到高效备考，最终实现提升学生的数学综合能力，发展学生数学核心素养水平的目标，是每一位高三教师面临的实际问题.高考试题很大程度上反应了当前的课改精神与教学导向，因此，聚焦核心素养，深度评析高考试题，分析试题特点对正确把握备考方向，找准高考脉搏，提高复习备考效率具有重要意义.本文对2013-2019年高考全国卷不等式选讲试题进行研究，并提出备考建议，为高三数学复习教学提供参考.

2考点回顾

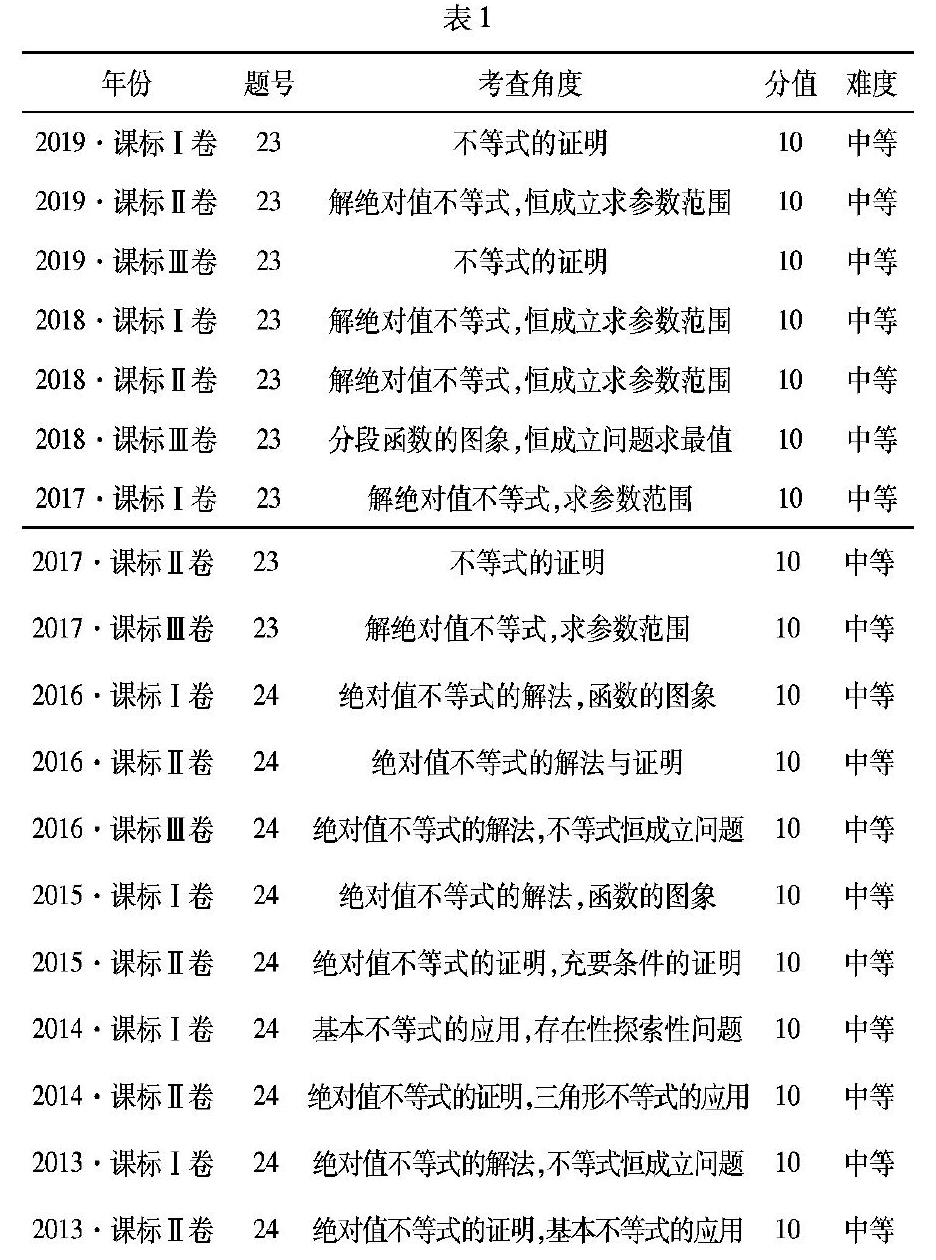
通过对2013-2019年全国卷进行整理分析，我们不难发现，这7年的“不等式选讲”试题无论在解题策略还是命题特点方面都有一定的规律性和稳定性.试题难度不大，但有一定的综合性与灵活性.试题的命题视角主要有：不等式的基本性质，含绝对值的不等式，不等式的证明等;考点主要集中在：含绝对值不等式的解法和不等式的基本性质的应用;命题立意主要体现在：利用不等式求最值，结合恒成立问题求参数的取值范围，利用基本不等式、重要不等式、柯西不等式等知识证明不等式等;试题渗透的数学思想方法主要有：转化与化归，分类讨论与数形结合;考查学科素养方面：重点聚焦逻辑推理，数学抽象和数学运算.

评析 例12-例18的求解，需要掌握不等式性质、理解基本不等式的本质内涵、了解柯西不等式的几种不同形式，理解它们的几何意义，深谙不等式中的分析法、综合法等证明方法，能够利用平均值不等式、柯西不等式求一些特定函数的最值.这些问题对综合运用所学知识分析和处理问题的能力要求高，难度大.

熟练掌握不等式的基本性质是解决不等式问题的前提和基础.基于高中数学中的重要不等式性质，探究基本不等式的前世与今生，准确理解基本不等式的成立条件，能够对其进行适当拓展，理解柯西不等式与权方和不等式的逻辑联系，做到心中不仅有数还有不等式演变和发展的整个过程，最后上升为心中有数还有形.

4 备考建议

4.1 紧扣考纲，夯实基础

认真研读课程标准和考试大纲，对“不等式选讲”部分的课标要求和考试说明做到心中有数，准确把握考纲涉及的每一个知识点，以及对应知识的要求层次，从而清晰地梳理出教学的重点与难点，精心设计教学素材和教学过程，重在夯实双基.根据学生实际学情严格把关课堂教学过程中的每一个关键点，在掌握基础知识的同时总结基本技能.近年高考全国卷对含绝对值不等式的考查，主要聚焦于不等式的性质、基本不等式的适用条件、绝对值不等式及有关定理和推论.

一轮复习阶段要侧重夯实双基，将重点、难点清晰地梳理出来，对照考纲要求，结合学生的实际学情，按照低起点、多梯度、抓落实的复习备考基本原则，有计划地引导学生对基础知识和基本技能进行重温和深化，初步形成基础知识体系，为下一阶段的思想方法深化和知识综合运用打下坚实基础.

二轮复习要抓主干知识，将一轮复习成果中的单个知识点串起来形成知识串，重点突出数形结合思想与分段讨论思想，深化学生对函数与方程、方程与不等式的逻辑关系的理解和掌握，帮助学生扫除知识点间的联系障碍，引导学生重点体会知识的发生与发展过程，初步形成网络化知识点.

三轮复习备考冲刺阶段，要突出对关键知识点和考纲重点要求的知识点进行强化，突破难点和关键点.含绝对值不等式的解法是近几年全国卷考查的热点，复习备考过程中，教师要重点引导学生对绝对值不等式的基础知识进行全方位的梳理，并带领学生搞清楚基础知识的来龙去脉，知其然更要知其所以然.可以参考以下做法.

思路1：可利用零点分段法求解，突出分类讨论的数学思想;

思路2：用好绝对值不等式的几何意义，突出基本思想与基本技能;

思路3：构造特殊函数，利用函数的图象及性质求解，突出转化与化归的的数学思想，渗透数形结合思想的同时深化函数与方程的思想.

强化利用分类讨论思想去掉绝对值符号，进而转化为分段函数的基本策略和解题思想，对典型问题的教学要注重立足于高考真题做好变式训练，强调一题多解和多题一解，重点发展学生利用数形结合思想解决实际问题的能力，总结绝对值不等式的一般解法，进而服务于恒成立问题、存在性问题的证明和处理.另外要突出基本不等式在证明不等式、处理恒成立问题、求函数最值、求参数取值范围等问题中的地位和作用.如果学生能力发展水平高、元认知发展水平较好，还可以对基本不等式进行拓展延伸，引导学生探索基本不等式与柯西不等式、权方和不等式之间的联系，帮助学生掌握重要不等式之间的逻辑联系和发展过程，以期能灵活运用相关不等式处理常见的不等式问题.

4.2 精选试题、精心设计，重在落实

精选试题是高效复习的基本前提，精心设计是有效教学的基本保证，重视落实方可达到高效复习的目标.考纲虽然包含柯西不等式内容，但近七年高考全国卷对不等式选讲部分的考查具有延续性和相对的稳定性：一方面考查绝对值不等式的解法与证明，以及恒成立问题求参数等常见问题;另一方面重点考查利用基本不等式证明较复杂不等式，函数恒成立问题求最值或是求参数范围等问题.

基于以上评析，预测2020年高考全国卷仍会重点考查含绝对值不等式的求解方法，以及利用基本不等式证明和处理恒成立问题，结合导数和函数图象性质求参数取值范围等，要重点关注不等式与函数的转化及其逻辑联系.在复习备考阶段所选试题可以重点突出上述内容.

4.3 样题参考

为方便大家备考，根据近7年高考试题的深度评析，给出以下样题供大家选编参考.

知識在运用中加深理解，技能在训练中逐渐提高，思想方法在变式训练中逐渐深化，理性思维在不断地解决问题的过程中培养.因此，在复习备考阶段，要聚焦核心素养，紧扣高考考查内容，精选试题、精心设计、精讲精练，方可达到精准复习、高效备考的目标.

参考文献：

[1]郝文华.不等式选讲试题的解题策略和教学启示[J].中学教研（数学），2019（02）：39-43.

[2]王印凡.2018年高考全国Ⅰ卷选做题分析及备考建议[J].中学数学研究（华南师范大学版），2018（17）：37-40.

[3]王沛钰.例谈含参数的绝对值不等式问题及其解法[J].中学数学教学，2018（04）：30-32.

（收稿日期：2019-06-17）