高考模拟题中的“广义组合数”

上海市七宝中学(201101) 李佳伟

1 试题呈现

试题(2016年上海市普陀区高三数学理科二模卷第14题)已知n∈ℕ∗，从集合{1,2,3,···,n}中选出k(k∈N,k≥2)个数j1,j2,···,jk，使之同时满足下面两个条件：

①1≤j1＜j2＜···＜jk≤n;

②ji+1-ji≥m(i=1,2,···,k-1)，则称数组(j1,j2,···,jk)为从n个元素中选出k个元素且限距为m的组合，其组合数记为例如根据集合{1,2,3}可得给定集合{1,2,3,4,5,6,7}，可得=____.

本题是一道创新题，考查的是对于新定义的理解.我们从组合数的定义看到，其含义是在n个元素中任意选取k个元素，并且任意两个元素之差大于等于m.如果m=1，即ji+1-ji≥1(i=1,2,···,k-1)，则就是通常意义下的组合数也就是说因此我们不妨把组合数称为“广义组合数”.那么，我们如何去思考这个问题呢?笔者经过一番研究，得出了几种解法，下面分享给大家.

2 试题的解法探究

解法一(枚举法)这里m=2，因此任意两个元素之差不小于2，易得如下组合：(1,3,5)，(1,3,6)，(1,3,7)，(1,4,6)，(1,4,7)，(1,5,7)，(2,4,6)，(2,4,7)，(2,5,7)，(3,5,7)总共10种组合，因此

枚举法的优点就在于思维量小，操作简单，缺点在于容易重复和遗漏.那我们试着寻求其他解法.

解法二由于任意两个元素之差不小于2，因此C(3,2)7就是相当于在1,2,3,4,5,6,7这7个数中选取3个不相邻的数的方法数.由于1≤j1＜j2＜j3≤7取自1,2,3,4,5,6,7，若j1,j2,j3互不相邻，则1≤j1＜j2-1＜j3-2≤5，由此可知从1,2,3,4,5,6,7中取3个互不相邻的数的选法与从1,2,3,4,5中选取3个不同的数的选法相同，即种.

解法三令j1=x1，j2-j1=x2，j3-j2=x3，则x1≥1，x2,x3≥2，x1+x2+x3=j3≤7，因此，原题可以转化为如下问题：

求x1+x2+x3=5，x1+x2+x3=6，x1+x2+x3=7这三个不定方程的整数解的个数之和，其中x1≥1，x2,x3≥2.为此，我们运用下列定理：

定理1不定方程x1+x2+···+xn=r的非负整数解的个数为

定理的证明见[1].

由于x1≥1，x2,x3≥2，我们作变量替换：y1=x1-1，y2=x2-2，y3=x3-2，则原问题又可以转化为求y1+y2+y3=0，y1+y2+y3=1，y1+y2+y3=2这三个不定方程的非负整数解的个数之和.根据定理1易得

3 结论推广

其中x1≥1，x2,x3,···，xk≥m，m(k-1)+1≤n，再令y1=x1-1，y2=x2-m，y3=x3-m，···，yk=xk-m，则计算的问题可以转化为求不定方程y1+y2+···+yk=0，y1+y2+···+yk=1，···，y1+y2+···+yk=n-mk+m-1的非负整数解的个数之和.根据定理1以及Pascal恒等式得：

结论总结：当m∈ℕ∗，且m(k-1)+1≤n，则

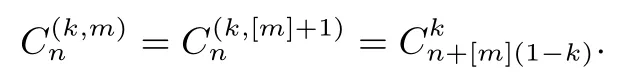
4 进一步探究

我们知道，通常意义下的组合数有许多有趣的性质，笔者想，广义组合数是否也有类似的性质呢?也就是说，通常意义下的组合数性质哪些是可以推广到广义组合数的呢?下面我们一起来探究.

性质1其中m∈ℕ∗，且m(k-1)+1≤n.

证明由得：

性质2

证明左边==右边.

性质3若n≥3，当n为奇数，当n为偶数，

证明当n为奇数，

广义组合数还有许多其他的性质，有兴趣的读者不妨做进一步探究.