含参函数中参数分类标准的选择与确定

福建省德化第一中学(362500) 吴志鹏

在解决含参函数问题时，经常要对参数进行分类转化，怎样分类，以什么标准进行分类，这是化解含参函数问题的难点也是关键点，只有突破这个关键点才能有效地解决相关的问题.下面我就一部分含参函数的分类标准的选择作如下归纳.

一、利用函数图象位置的特殊性，确定分类标准

函数的解析式或函数图象会因为参数的改变而发生变化，因此我们在确定参数的分类标准时，常常要去寻找使得函数产生变化的那些特殊点、特殊值或者是一些特殊的位置，因为它们是函数解析式或函数图象产生变化的临界点或临界值.

1.参照特殊值，确定分类标准

例1设函数f(x)=|x-1|+|x-a|，对于∀x∈ℝ，f(x)≥2，求a的取值范围？

分类思路函数的解析式中含有|x-1|和|x-a|两个绝对值，当a=1，两个式子相同，此时为函数的一种特殊情况即f(x)=2|x-1|，所以a=1是使函数解析式、图象产生变化的一个临界值，据此我们可确定函数的分类标准即按a＜1，a＞1，a=1三种情况来进行分类．

解析当a=1时，f(x)=2|x-1|不满足题设条件，舍去;当a＜1时，f(x)=|x-1|+|x-a|根据去绝对值符号的法则可得：

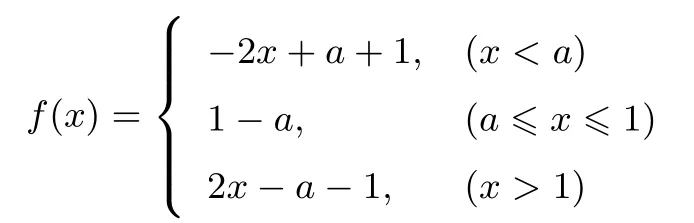
由函数的图象可知：f(x)min=1-a，要使f(x)≥2对于∀x∈ℝ都成立，只需1-a≥2，即a≤-1，又因为a＜1，所以a≤-1;当a＞1时，f(x)=|x-1|+|x-a|，去绝对值符号可得：

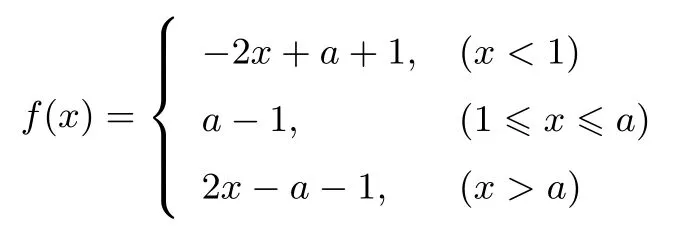
由函数的图象可知：f(x)min=a-1，要使f(x)≥2对于∀x∈ℝ都成立，只需a-1≥2，即a≥3，又因为a＞1，所以a≥3.所以对于∀x∈ℝ，f(x)≥2，a的取值范围是a≤-1或a≥3．

变式讨论函数2a)x+1的单调性．

分类思路由于

f′(x)=x2-(3a+1)x-(2a2+2a)=(x-2a)[x-(a+1)],此时导函数有两个零点2a和a+1且不能确定大小关系，令2a=a+1即a=1，找到了区分零点大小的依据，a=1即为参数分类标准的一个临界值，由此而确定出函数中参数要按：a＞1，a=1，a＜1三种情况进行分类．

结论：当a＞1时，f(x)在(-∞,a+1)，(2a,+∞)单调递增，在(a+1,2a)单调递减；当a=1时，f(x)在ℝ上单调递增；当a＜1时，f(x)在(-∞,2a)，(a+1,+∞)单调递增，在(2a,a+1)单调递减．

2.根据特殊点，确定分类标准

例2已知f1(x)=1-ax，f2(x)=(1-x)a-1，以max{m,n}表示两数m,n中较大者，设f(x)=max{f1(x),f2(x)}，试求f(x)的解析式?

分类思路两个函数均为一次函数，其图象是两条平行直线或重合直线，此时两直线在y轴上的截距对应的点成了区分函数值大小的一个临界点，自然成了确定参数分类的标准.由f1(x)=f2(x)得a=2，函数值的大小比较可按a＜2，a=2，a＞2三种情况进行讨论：

解析因为f1(x)-f2(x)=2-a，则按a＜2，a=2，a＞2分类得：f(x)==

3.按特殊位置，确定分类标准

例3(2017年高考课标I卷理科第21题)已知函数f(x)=ae2x+(a-2)ex-x.

(1)讨论f(x)的单调性；

(2)若f(x)有两个零点，求a的取值范围．

解析(1)f(x)的定义域为(-∞,+∞)，f′(x)=2ae2x+(a-2)ex-1=(aex-1)(2ex+1).若a≤0，则f′(x)＜0，所以f(x)在(-∞,+∞)单调递减；若a＞0，则由f′(x)=0得x=-lna，所以当x∈(-∞,-lna)时，f′(x)＜0；当x∈(-lna,+∞)，f′(x)＞0，所以f(x)在(-∞,-lna)单调递减，在(-lna,+∞)单调递增；

(2)根据第(1)题，若a≤0，f(x)至多有一个零点，若a＞0，当x=-lna时，f(x)取得最小值，求出最小值

分类思路此时函数的最小值所对应点的位置决定了函数图象与x轴交点的个数，当即a=1，此时函数图象的最低点落在x轴上，由此可确定分类的标准为函数图象的最低点分别落在x轴上、x轴上方和x轴下方，并由此获得参数a的分类标准，即按a=1，a＞1和0＜a＜1三种情况进行讨论．

解析(1)当a=1，由于f(-lna)=0，故f(x)只有一个零点；

4.据根判别式，确定分类标准

一元二次方程根的判别式是研究一元二次方程是否存在实根的重要依据，也是二次函数图象与x轴位置关系的判断依据，同样根的判别式对求解一元二次不等式也有着不可或缺的作用．所以对于函数中出现的含有参数的二次式，我们经常可利用判别式的三种情况即Δ＜0，Δ=0，Δ＞0来确定参数的分类标准．

例4(2018年高考全国I卷理科第21题节选)已知函数讨论f(x)的单调性．

分类思路函数f(x)的定义域为(0,+∞)，f′(x)=由于x＞0，导函数的符号与g(x)=-x2+ax-1的符号相关，则可按g(x)≤0和g(x)＞0两种情况进行分类讨论，进而转化为利用二次函数根判别式，即Δ≤0和Δ＞0来确定参数的分类标准．

解析f(x)的定义域为设g(x)=-x2+ax-1，

(i)当Δ≤0时，即a≤2，此时g(x)=-x2+ax-1≤0，所以有f′(x)≤0，当且仅当a=2，x=1时f′(x)=0，所以f(x)在(0,+∞)单调递减.

(ii)当Δ＞0时，即a＞2，令f′(x)=0得，或当x∈时，f′(x)＜0；当时，f′(x)＞0，所以f(x)在单调递减，在单调递增．

二、依函数解析式参数符号意义，确定分类标准

参数的符号经常会对函数值的符号的产生直接的影响，如aex，当a＞0时，aex＞0；当a＜0时，aex＜0；当a=0时，aex=0，同样的参数的符号对函数的图象也会产生影响，如一次函数y=kx+b，k＞0时，函数单调递增，k＜0时，函数单调递减；又如二次函数y=ax2+bx+c(a0)，当a＞0时二次函数的图象开口向上，a＜0二次函数的图象开口向下，由于参数符号对函数图象变化的影响，所以有时我们也可利用参数的符号来确定分类的标准．

例5(2017年高考课标I卷文科第21题节选)已知函数f(x)=ex(ex-a)-a2x，讨论f(x)的单调性；

分类思路由于函数f(x)的定义域为(-∞,+∞)，f′(x)=2e2x-aex-a2=(2ex+a)(ex-a)，此时两个因式的符号是不确定的，由于ex＞0，所以参数a的符号决定了导函数的符号，从而影响了函数的单调性，由此确定了函数的分类标准，可按a=0，a＞0，a＜0三种情况分类，进行讨论.

解析①若a=0，则f′(x)=2e2x＞0恒成立，此时f(x)在(-∞,+∞)单调递增．

②若a＞0，此时2ex+a＞0，则由f′(x)=0得x=lna．当x∈(-∞,lna)时，f′(x)＜0；当x∈(lna,+∞)时，f′(x)＞0，所以f(x)在(-∞,lna)单调递减，在(lna,+∞)单调递增．

③若a＜0，此时ex-a＞0，则由f′(x)=0得时，f′(x)＜0；当x∈时，f′(x)＞0，故f(x)在单调递减，在单调递增．

例6(2017年高考课标Ⅲ卷文科第21题节选)已知函数f(x)=lnx+ax2+(2a+1)x，讨论f(x)的单调性；

分类思路函数导数由于函数的定义域为{x|x＞0}，则有此时导函数符号取决于参数a的符号，由此可确定函数的分类标准，即按a≥0，a＜0两种情况进行讨论．

结论：当a≥0时，f′(x)≥0，则f(x)在(0,+∞)单调递增，当a＜0时，则f(x)在单调递增，在单调递减．

三、由最值点与区间的动定关系，确定分类标准

确定曲线在某个区间的最(极)值问题，我们可先确定曲线最(极)值点位置与区间位置两者之中已确定的位置，即弄清问题中的动定关系，其中不含参数的最值点(区间端点)其位置为已经确定的，含参的区间端点(最值点)的位置为可变的，此时可将可变的图象(区间)沿x轴进行平移，使之通过确定的区间(图象)，再由通过时的关键位置来确定参数的分类标准．

例7求函数f(x)=-x2+2ax+1-a在0≤x≤1的最大值g(a)．

分类思路配方得f(x)=-(x-a)2+a2-a+1此时二次函数图象的开口向下，对称轴为直线x=a(a待定)，也是函数最值取得的位置，而区间[0,1]却是确定的，这时我们可利用动直线和确定区间的位置关系来选择对称轴的放置位置，由此产生参数a的分类标准即参数a可按：a＜0，0≤a≤1，a＞1三种情况进行分类．

解析(1)当a＜0，f(x)在x∈[0,1]单调递减，所以g(a)=f(x)max=f(0)=1-a;

(2)当0≤a≤1，g(a)=f(x)max=f(a)=a2-a+1;

(3)当a＞1，f(x)在x∈[0,1]单调递增，所以g(a)=f(x)max=f(1)=a.

变式1函数f(x)=alnx(a＞0)，e为自然对数的底数．若f(x)在(1,e)上有恒成立，求实数a的取值范围．

分类思路因为x∈(1,e)，恒成立，即f(x)-x+1＞0恒成立.令h(x)=alnx-x+1(x＞0)，即h(x)min＞0，因为令h′(x)＞0，得0＜x＜a；h′(x)＜0，得x＞a，所有当x=a，h(x)取得极大值，此时区间(1,e)确定，而极大值点x=a的位置待定.现只需分情况将极大值点x=a的位置置于区间(1,e)的位置左右两侧和区间内部进行讨论.即参数的分类标准可确定为a＞e，1≤a≤e和a＜1三种．

1)当a＞e时，h(x)在(1,e)上为增函数，h(x)＞h(1)=0;

2)当1≤a≤e时，h(x)在(1,a)上为增函数，在(a,e)上为减函数，此时只须即a≥e-1．

3)当a＜1时，h(x)在(1,e)上为减函数，h(x)≥h(e)=a+1-e＜0，不符合题意.

综上所得：a≥e-1．

变式2当t≤x≤t+1时，求f(x)=x2-2x-1的最小值?

分类思路变式2将例题中区间确定对称轴待定的情况改变为对称轴确定而区间待定，即二次函数f(x)=x2-2x-1图象的对称轴为直线x=1(最小值点所在的位置)而区间[t,t+1]由于t的未知而待定，此时只需利用对称轴的特殊位置来置放区间，问题便可迎刃而解，并由此而取得参数的分类标准，可按t+1＜1，t≤1≤t+1，t＞1即t＜0，0≤t≤1，t＞1三种情况来类.(解法略)

对于上述二次函数的两类问题我们也可迁移到含有极值点的函数问题，即极值点的位置不确定而区间确定的函数最值问题和极值点的位置确定而区间不确定的函数最值问题来解决．

总之，对于含有参数，需要进行分类的函数，选择分类的标准很重要，是一个难点问题，所以教师在授课时，应注意讲清这个标准是从哪里来，隐藏在题目的哪些信息中，要让学生知其所以然，要让学生在选择参数的分类标准，做到有据可查，这样学生在分类的过程中才不至于混乱，找不着头绪.其实分类的标准远不止以上这几类，它需要我们在实践的过程中，学会观察，善于发现，找到影响函数值的符号、图象等出现变化的参数情况，从而找到参数的分类标准，更好地解决相关的函数问题．