2019年高考立体几何专题命题分析

云南省云南师范大学数学学院(650500) 唐明超

广东省东莞市麻涌中学(523000) 骆妃景

广东省汕头市澄海华侨中学(515800) 潘敬贞

立体几何是高中数学的主干知识，也是几何学的基础，它具有难度大、逻辑性强等特点，承载着培育学生数学抽象、逻辑推理、直观想象、数学建模、数学运算等核心素养的育人功能，从而成为历年高考数学的热点问题，也是高考的重点和难点.从认识多面体与旋转体的结构特征出发，聚焦点、直线、平面的位置关系，落脚在点、线、面位置关系的判定及空间角与距离的计算.试题往往以选择题、填空题、解答题的形式呈现，紧紧围绕课标要求，历年考题题型相对稳定，承载着高考的选拔性功能，既注重基础又突出能力.

一、试题内容分析

1.考点解读

表1

2019年文12，17 18正四棱锥与圆柱内接;线面平行，线面垂直，线面角.1道填空题，1道解答题.12题易17题中天津卷理11，17 18正四棱锥与圆柱内接;直线与平面平行，线面角，二面角.1道填空题，1道解答题.11题易17题中2019年浙江卷4，8，19 23三视图;异面直线所成角、直线和平面所成角和二面角.2道选择题，1道解答题.4题中8题难19题难2019年江苏卷9，16 19棱锥的体积计算;线面平行、线线垂直的证明.1道填空题，1道解答题.9题易16题中2019年春季15，17 19线线、线面位置关系的判定;线线角，锥体体积计算.1道选择题，1道解答题.15题易17题易上海卷秋季14，17 19旋转体与体积计算;点到面的距离，线面角.1道选择题，1道解答题.14题易17题易

选择题与填空题重点考查对公理及定理的理解和简单运用，往往以常见多面体的三视图、圆柱、圆锥、球等问题为背景考查几何量的计算，重点考查画图、识图、用图的能力;解答题重点考查空间中线线、线面、面面位置关系的判定，以及线面角、面面角、点到面的距离计算.多以中等难度试题呈现，重点考查基础知识与基本技能，渗透部分数学文化考题和实际应用背景问题，突出试题的思想性和知识点的实际应用价值，具有较好的教学导向作用，体现立德树人的根本任务要求.

2.题目设置与分值对比分析

2019年全国I卷试题总共设置两个题，分值17分，一个填空题一个解答题;2019年全国II卷、III卷设置了三个题，选择填空解答各一题，分值22分;北京卷设置了两个填空题和一个解答题，分值高达24分;天津卷设置一个填空题一个解答题，分值18分;浙江卷设置两个选择题一个解答题，试题难度相对较大，分值23分;江苏卷和上海卷风格相近，均设置一个小题一个大题，分值19分，整体难度不大，属于中等难度偏下的题目.

从表1可以看出立体几何知识在高考试卷中的比重稳定在17-24分之间，占整套试卷比重的10%以上，足以看出各省对立体几何知识的重视程度;题目设置具有一定的规律性，选择题填空题往往位于客观题的后段，解答题往往设置在主观题的前三题，难度随题号的增大有增大的趋势.

3.试题内容归类

试题内容可大致分为以下四类.一是以球、圆柱、圆锥等常见的特殊旋转体的体积计算为主;二是已知三视图还原几何体并求出几何体的体积;三是点线面位置关系的判定与证明;四是线线角、线面角、面面角的计算.题目设置相对常规，都是学生常见的模型，背景均源于生活，源于教材.

也有部分源于数学文化背景的试题，如全国II卷的第16题，源于中国古代的金石文化，以印信为载体，考查多面体的结构特征以及多面体棱长计算.还有与物理学科交叉的问题，如全国III卷第16题，虽然背景与物理学科交叉，但是载体还是多面体，虽然都设置在第16题，但是难度并不大，要求考生具有较强的阅读理解能力和数学建模能力.

全国14套试卷只有北京卷和浙江卷考查了三视图，这也说明高考的命题趋势紧紧扣住2017版新课程标准，这与新课改中要求删除三视图有一定的关系.只有全国I卷和全国II卷涉及球的问题，这也是全国卷的特点，继承了全国卷喜欢考查多面体与球的切接问题的传统.

4.文理科试题对比分析

从难度上看，文科试题整体比理科试题简单，这也与当下文科生与理科生的实际学情相关，但是文理科同题的情况很明显，几乎所有涉及文理分科的考卷都有文理同题的情况，比重较2018年以前大，这或许也在释放文理不分科以及缩小文理科试题难度差异的重要信号.从试题内容上看，客观题基本属于文理同题，主观题文科没有考查二面角，但是都有文理科同背景同题的情况，这也说明文理科试题在内容上的差异越来越小.从题量和分值占比上看，文理科试题没有差异，均是相同的题量相同的分值.从素养考查角度来看，文理科没有明显差异.

5.核心素养考查分析

试题重点考查数学抽象、逻辑推理、数学运算、直观想象、数学建模等核心素养.具有综合考查的特点，即同一道试题既考查数学抽象又考查逻辑推理，还考查数学运算，这与素养的发展规律相适应，在尊重学生个体差异的基础之上，结合学生的元认知发展水平，充分体现知识的发生与发展逻辑.这也提示我们在平时的教学过程中一定要注重核心素养的渗透和培育，核心素养虽然看不见摸不着，但是要善于借助学习素材将核心素养的培育化无形为有形，潜移默化，真正体现在学生的发现并提出问题、思考并解决问题的关键能力上来、发展学生的思维能力，最终形成适应社会发展所必需的品格.

二、命题意图分析

2019年高考数学立体几何试题立足知识的本质和基础，聚焦思想方法，着重考查核心素养，试题整体体现了数学学科特点，凸显育人功能，具有很好的区分度，能够很好的承担选拔人才的功能.部分试题在知识点交汇处命题，还首次尝试与学科交叉命题，将立体几何知识赋予鲜活的生命，实现了立体几何知识考查应有的深度和广度.

1.重主干，考基础

从空间几何体的结构特征到三视图，从点线面位置关系的判定到给以严格证明，从两直线所成的角到线面角再到面面角的证明与求解，试题的命制突出立体几何知识主干，没有特意强调某一部分或者规避某一知识点，只是随着新课改的深入，在以往命题的基础之上将部分知识点进行融合，既体现高考试题知识点覆盖面广，又能很好的体现立体几何知识的功能和作用.部分试题重点考查学生的识图和画图能力，要求学生经历观察、猜想、证明的逻辑推理过程.从知识立意到能力立意的转变也是2019年立体几何试题的一个显著特征，紧扣考试说明又不拘泥于考纲，不仅突出考查学生的空间想象能力，还重在考查学生的逻缉思维能力和推理论证能力.

例1(2019年高考全国I卷理科第18题)如图1，直四棱柱ABCD-A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E,M,N分别是BC,BB1,A1D的中点.

(1)证明：MN//平面C1DE;

(2)求二面角A-MA1-N的正弦值.

图1

图2

解(1)如图2，过N作NH⊥AD，则NH//AA1，且又MB//AA1，所以四边形NMBH为平行四边形，则NM//BH，由NH//AA1，N为A1D中点，得H为AD中点，而E为BC中点，所以BE//DH，BE=DH，则四边形BEDH为平行四边形，则BH//DE，所以NM//DE，因为NM/⊂平面C1DE，DE⊂平面C1DE，所以MN//平面C1DE;

(2)以D为坐标原点，以垂直于DC的直线为x轴，以DC所在直线为y轴，以DD1所在直线为z轴建立空间直角坐标系，则N有设平面A1MN的一个法向量为m=(x,y,z)，由取y=得又平面MAA1的一个法向量为n=(1,0,0)，所以即二面角A-MA1-N的正弦值为

例2(2019年高考全国I卷文科第19题)如图1，直四棱柱ABCD-A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E,M,N分别是BC,BB1,A1D的中点.

(1)证明：MN//平面C1DE;

(2)求点C到平面C1DE的距离.

解(1)同例1第(1)小题，解答略;

(2)过C作C1E的垂线，垂足为H.由已知可得DE⊥BC,DE⊥C1C，所以DE⊥平面C1CE，故DE⊥CH.从而CH⊥平面C1DE，故CH的长即为C到平面C1DE的距离，由已√知可得CE=1，C1C=4，所以故从而点C到平面C1DE的距离为

评析以直四棱柱这个熟悉的几何体为背景，考查线面平行的证明，二面角的计算以及求解点到平面的距离，突出主干知识，重在考查基础知识与基本技能，题目设置较常规;理科试题起点较低，入口宽，有意识的引导学生利用空间向量坐标运算求解二面角，在建立直角坐标系时选择面广，不同的学生可能会建立不同的坐标系，这在一定程度上也体现了高考试题的思想性和方法性.对于文科试题而言，既可以考虑直接找点到平面的垂线段，从而利用平面几何知识直接求解，还可以考虑学生常用的等体积法求解，甚至可以借助空间直角坐标系用坐标运算实现解题.

例3(2019年高考全国II卷文科第17题)如图3，长方体ABCDA1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.

图3

(1)证明：BE⊥平面EB1C1;

(2)若AE=A1E，AB=3，求四棱锥E-BB1C1C的体积.

解(1)证明：由长方体ABCD-A1B1C1D1可知，B1C1⊥平面ABB1A1，BE⊂平面ABB1A1，所以B1C1⊥BE，所以BE⊥EC1，B1C1∩EC1=C1，所以BE⊥平面EB1C1;

(2)由(1)知∠BEB1=90°，由题设可知Rt△ABERt△A1B1E，所以∠AEB=∠A1EB1=45°，所以AE=AB=3，AA1=2AE=6，因为在长方体ABCD-A1B1C1D1中，AA1//平面BB1C1C，E∈AA1，AB⊥平面BB1C1C，所以E到平面BB1C1C的距离d=AB=3，所以四棱锥E-BB1C1C的体积

例4(2019年高考全国II卷理科第17题)如图3，长方体ABCD-A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.

(1)证明：BE⊥平面EB1C1;

(2)若AE=A1E，求二面角B-EC-C1的正弦值.

解(1)同例3;

(2)以C为坐标原点，CD所在直线为x轴，CB所在直线为y轴，CC1所在直线为z轴，建立空间直角坐标系，设AE=A1E=1，因为BE⊥平面EB1C1，所以BE⊥EB1，因为AB=1，则E(1,1,1)，A(1,1,0)，B1(0,1,2)，C1(0,0,2)，C(0,0,0)，因为BC⊥EB1，所以EB1⊥面EBC，故取平面EBC的法向量为设平面ECC1的法向量n=(x,y,z)，由得取x=1，得n=(1,-1,0)，所以所以二面角B-EC-C1的正弦值为

评析相比例1与例2，例3与例4的几何体明显简单很多，从底面是菱形进一步特殊为底面是正方形，设问方式从证明线面平行到线面垂直，换汤不换药，出发点都是考查学生对点线面位置关系的理解和应用，属于学生较为熟悉的问题;文科试题的第(2)小题要求计算四棱锥的体积，理科试题要求求解二面角的正弦值，都属于常规问题，题目起点低难度小，注重考查四基与四能，如能用好空间直角坐标系，还可以给试题的解答赋予更优化的方法，关键看学生如何选择使用.

2.题型相对稳定，不偏不怪

例5(2019年高考上海卷秋季第15题)已知平面α、β、γ两两垂直，直线a、b、c满足：a⊆α，b⊆β，c⊆γ，则直线a、b、c不可能满足以下哪种关系()

A.两两垂直 B.两两平行 C.两两相交 D.两两异面

解利用面面垂直的性质，既可以画图判定也可以就生活中的实物模型进行判断，比如常见的长方体和正方体中的线面位置关系等，正确答案为B.

例6(2019年高考江苏卷第9题)如图4，长方体ABCD-A1B1C1D1的体积是120，E为CC1的中点，则三棱锥E-BCD的体积是____.

解因为长方体ABCD-A1B1C1D1的体积是120，E为CC1的中点，所以VABCD-A1B1C1D1=AB×BC×DD1=120，所以×BC×DC×CE=10.

图4

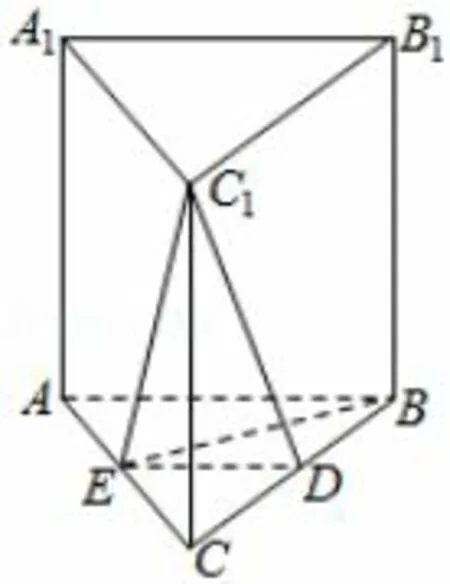
图5

例7(2019年高考江苏卷第16题)如图5，在直三棱柱ABC-A1B1C1中，D,E分别为BC,AC的中点，AB=BC.求证：

(1)A1B1//平面DEC1;

(2)BE⊥C1E.

解(1)因为在直三棱柱ABC-A1B1C1中，D,E分别为BC,AC的中点，所以DE//AB，AB//A1B1，所以DE//A1B1，因为DE⊂平面DEC1，A1B1/⊂平面DEC1，所以A1B1//平面DEC1.

(2)因为在直三棱柱ABC-A1B1C1中，E是AC的中点，AB=BC.所以BE⊥AA1，BE⊥AC，又AA1∩AC=A，所以BE⊥平面ACC1A1，因为C1E⊂平面ACC1A1，所以BE⊥C1E.

评析例5、例6、例7均选自新课改首批试验省份的高考试题，仔细分析可以看出题目难度不大，突出考查基础知识;题型较稳定，背景均为常见的几何体，问题设置主要是考查线面平行、线线垂直的证明，围绕空间中线线、线面、面面间的位置关系进行设置，不生硬，学生易于接受;计算量并不大，突出“多想少算”的命题趋势.从侧面亦可反映出高考改革对立体几何的要求是注重对几何体基本几何关系的理解和掌握，会判断线线、线面、面面位置关系，并能给出严格的推理论证.

3.紧扣课标要求，立足教材

《2017年版普通高中数学课程标准》明确指出可借助长方体认识和理解空间点、直线、平面的位置关系;学会用数学语言描述有关平行与垂直的性质和判定，并能证明一些结论;了解简单几何体表面积和体积的计算方法，运用直观感知、操作确认、推理论证、度量计算等认识空间图形的性质，建立空间观念.所以试题的命制往往基于空间图形的基本几何性质，以检测学生的空间想象能力和空间观念为主，注重基础，突出几何学的发展历程，强化空间向量的工具性.

例8(2019年高考北京卷理科第16题)如图6，在四棱锥P-ABCD中，PA⊥平面ABCD，AD⊥CD，AD//BC，PA=AD=CD=2，BC=3.E为PD的中点，点F在PC上，且

(1)求证：CD⊥平面PAD;

(2)求二面角F-AE-P的余弦值;

图6

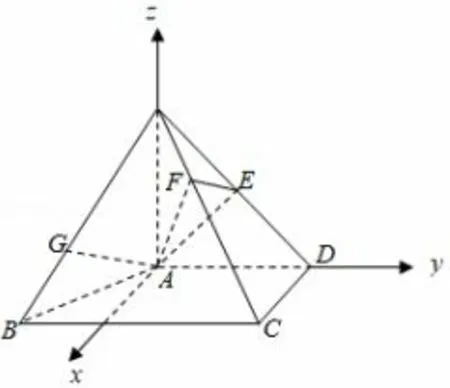
图7

解(1)证明：因为PA⊥平面ABCD，所以PA⊥CD，因为AD⊥CD,PA∩AD=A，所以CD⊥平面PAD.

(2)以A为原点，在平面ABCD内过A作CD的平行线为x轴，AD为y轴，AP为z轴，建立空间直角坐标系，A(0,0,0)，E(1,0,1)，P(0,0,2)，平面AEP的法向量n=(1,0,0)，设平面AEF的法向量m=(x,y,z)，则取x=1，得m=(1,1,-1)，设二面角F-AE-P的平面角为θ，则cosθ=所以二面角F-AE-P的余弦值为

(3)直线AG不在平面AEF内，理由如下：

题源1(人教A版普通高中数学课程标准实验教科书选修2-1第109页例4)如图8，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，点E是PC的中点，作EF⊥PB交PB于点F.

图8

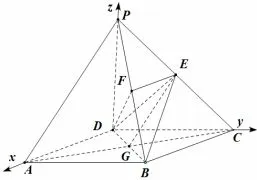
图9

(1)求证：PA//平面EDB;

(2)求证：PB⊥平面EFD;

(3)求二面角C-PB-D的大小.

解(1)以D为坐标原点，设DC=1，建立如图9所示的空间直角坐标系.依题意得A(1,0,0)，P (0,0,1)，E(0,0.5,0.5)，连接AC与BD相交于点G，从而且所以即PA//EG.而EG⊂平面EDB，且PA/⊂平面EDB，因此PA//平面EDB.

(3)已知EF⊥PB，由(2)可知DF⊥PB，故∠EFD是二面角C-PB-D的二面角.设F(x,y,z)，则(x,y,z-1).因为得x=k,y=k,z=1-k.因为得所以所以由cos∠EFD=所以∠EFD=60°，即二面角C-PB-D的大小为

评析例8能较好的反映课标要求，虽然没有直接给出底面是直角梯形，但是结合已知条件，学生很容易判断底面是一个直角梯形，而且相关的边角关系也很容易求出，基于学生已有知识经验和空间观念不难建立空间直角坐标系，甚至有学生基于基本活动经验能够很轻松的将该四棱锥补成直四棱柱，进而在一个更加熟悉且更加常规的几何体中研究线线、线面、面面位置关系，通过空间直角坐标运算，学生容易得出此题答案，关键是考查学生的数学运算能力.

题源1与例8相似度很高，可以看成是类题，例8只是将底面是正方形换成一个直角梯形，本质上没有改变其空间关系，设问方式基本相同，只是求证的命题不同，解决问题的原理及方式相同，空间直角坐标系的建系方式基本一样.这也在暗示着平时的学习过程一定要注意回归教材，将教材内容吃透，将教材的典型例题和习题进行深入研究，注重在教材例题与习题的基础之上合理拓展变式，赋予教材内容灵魂和活力;研究教材不是为了押题，更不是为了寻求所谓的“秒杀技”，只是为了能够更好的领悟教材编写者的意图，弄清问题本质，寻求解决问题的一般方法，以期能够以不变应万变，真正意义上提升数学素养.

例9(2019年高考北京卷文科第13题理科第12题)已知l,m是平面α外的两条不同直线.给出下列三个论断：①l⊥m;②m//α;③l⊥α.

以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：____.

解因为l,m是平面α外的两条不同直线，所以由线面平行的判定定理得：若l⊥α,l⊥m，则m//α.故答案为：若l⊥α,l⊥m，则m//α.

题源2(人教A版普通高中数学课程标准实验教科书必修2第72页练习第2题)已知直线a,b和平面α，且a⊥b,a⊥α，则b与α的位置关系是____.

解根据线面垂直的基本性质可知b与α的位置关系是平行或者直线在平面内.

评析例9可借助长方体这个特殊的几何体进行判断，考查学生的想图、作图、识图的基本素养;紧扣课标要求，聚焦直线与平面垂直的性质，综合空间中线线、线面的位置关系进行判断，目的在于检测学生运用直观感知、操作确认、推理论证解决立体几何问题的关键能力，考查学生的数学抽象和逻辑推理数学素养.

例9就是题源2的变式，在考查学生的基础知识掌握情况和数学抽象思维能力等方面意义重大，一方面体现新课标的导向是回归课本、研究课本;另一方面也说明新课标注重对数学知识网络的构建，要求学习数学的过程一定要注重知识的发生与发展过程，弄清楚问题从何而来，有何用处，要到哪里去.

4.突出多想少算，注重考查核心素养

例10(2019年高考全国II卷文理同题第16题)中国有悠久的金石文化，印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”.半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图10右图是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1.则该半正多面体共有____个面，其棱长为____.

图10

解该半正多面体共有8+8+8+2=26个面，设其棱长为x，则解得故答案为：26，

评析数学文化的渗透既可以体现学科育人价值，又可以传承和弘扬中国优秀传统文化，还可以让学生逐渐感受到数学的美学价值和实际应用价值，发展学生的情感态度价值观;更重要的是在整个思考并解决问题的过程中，既可以考查和发展学生的数学抽象、直观想象、数学建模等核心素养，又可以考查学生发现并提出问题、思考并解决问题的能力.例10设置在最后一个填空题，给人的印象是小题的压轴题，但是运算过程并不复杂，真正意义上体现了“多想少算”这一新课标指引下的命题方向，从平面上升到三维空间的过程学生容易感知与理解，但是从三维降至二维就要求学生具有较好的逆向思维能力和数学抽象能力，这也提示广大教育教学工作者在平时的教学过程中要注重引导学生从二维至三维互相转化的空间想象能力的培养，渗透转化与化归的数学思想，帮助学生提高解决实际问题的能力.

三、热点解读

1.几何体基本量的计算问题

从2019年高考试题可以看出立体几何基本量的计算仍然是考查的重点和问题解决的落脚点，多面体的体积计算多出现在小题中，往往以三视图为背景考查几何体的还原能力，并能根据三视图的边长关系准确得出原几何体的棱长，进而计算几何体的体积或表面积.另外，多面体与球的切接问题也是全国卷高考的热点问题，主要聚焦于球心位置的确定和半径的计算，对学生的数学抽象思维能力要求较高，一般的处理思路就是通过补体寻找多面体与球的载体，进而借助常见的几何体如正方体与长方体的外接球或内接球的基本特点确定球心和半径.

2.点线面位置关系的证明问题

点线面位置关系的证明多以线面平行、线面垂直的形式呈现，既考查线面平行或垂直的判定定理，也考查线面平行或垂直的性质定理，要求学生对判定定理和性质定理做到清楚认识和准确理解，掌握它们之间的逻辑联系，并能优化数学语言表达能力实现严密的逻辑推理.题目呈现方式多以解答题的形式出现，着重考查转化与化归的数学思想;几何法与向量法是解决该类问题的两种基本方法，向量法尤其能够体现其工具性价值，是解决立体几何证明问题的有力工具，但是对数学运算核心素养要求较高，需要在平时的学习过程加以适当的训练，提高运算能力.

3.空间角及距离的计算问题

线面角的寻找、证明、平面化求解也是文理科立体几何解答题的热点之一，既可以直接用几何法进行证明并计算，也可以借助空间直角坐标系通过向量的坐标运算进行求解，两种处理思路各有优缺点，考生可以根据个人实际情况灵活选择.

二面角的计算多出现在理科试题中，对学生的思维能力和逻辑推理能力要求较高，处理策略一般是“找—证—求”，优点就是运算量少，但是往往思维量较大;如果能够正确并合理的建立空间直角坐标系，通过坐标运算实现问题的解决可以有效避免较复杂的逻辑推理过程，但是往往对学生的运算能力要求较高;总之几何法与向量法各有优缺点，两种方法都需要灵活掌握，合理选择.

四、2020年高考备考建议

1.再读课标，明确方向

课程标准是教与学的参考依据，是教育教学专家精心研究制定的，具有高度的理论意义和实践价值.研读课标要求没有终点只有不断的起点，以课标要求指导教学与学习能确保方向不偏，参考考试说明，认真研究教材和高考试题，做到心中有纲，学习有度，立足四基，着重发展四个能力.尊重学生认知发展规律的同时尊重知识的发生与发展过程，追本溯源，引导学生在经历知识的发生与发展过程中理解问题的本质并准确构建知识网络，提升综合运用所学知识解决实际问题的能力.学习的目的是为了发展学生适应社会发展所必需的关键能力和必备品格，最终落脚点是提高解决问题的能力.

2.抓主干、突出问题本质

从考点分布可以看出，高考考查的知识点覆盖面广，但均以主干知识为命题主线，所以学习的过程应该突出主干知识，在掌握基础知识和主干知识的前提下拓宽知识面，丰富知识内涵，探究问题本质，掌握基本思想方法，提升关键能力.

3.注重核心素养的渗透

核心素养的落实要体现过程性和循序渐进性，要将核心素养的培育渗透到数学知识的学习过程中，发展能力就是发展素养，立体几何专题是最能够全面培育和发展数学核心素养的知识板块，以特殊模型为载体，通过多角度的变式探究，帮助学生体会并挖掘问题的本质和知识发展的一般规律，强化几何体的切割与补体思想，在切与补的过程中感悟几何体间的逻辑联系.

4.强化数学语言表达能力

数学语言的表达能力在很大程度上可以体现数学素养的发展水平，所以在平时的教学过程中，除落实双基外还要重视推理过程的规范训练，数学是一门严谨的学科，逻辑推理讲究严密性和完整性.从应试的角度看，推理过程的完整性与书写的规范性决定着考试分数，适当的板演与示范就显得尤为重要.