莫为浮云遮望眼拨开迷雾见真颜—对2019年高考浙江卷第21题的探究

广东省佛山市乐从中学(528315) 林国红

每年都有不少的优质高考试题，这些试题都是命题专家精心设计的杰作，凝聚了命题专家的集体智慧，对中学教学有良好的导向性，值得我们去品味.要充分认识高考题所蕴含的价值，挖掘高考题的功能，发挥其内在作用，并以此来促进教学.

下面笔者以今年浙江省高考的解析几何大题为例，进行详细解答与分析，并进行探究，供大家参考，希望能抛砖引玉.

一、题目呈现与分析

题目(2019年高考浙江卷第21题)如图1，已知点F(1,0)为抛物线y2=2px(p＞0)的焦点，过点F的直线交抛物线于A,B两点，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且Q在点F右侧.记△AFG,△CQG的面积分别为S1,S2.

(1)求p的值及抛物线的准线方程;

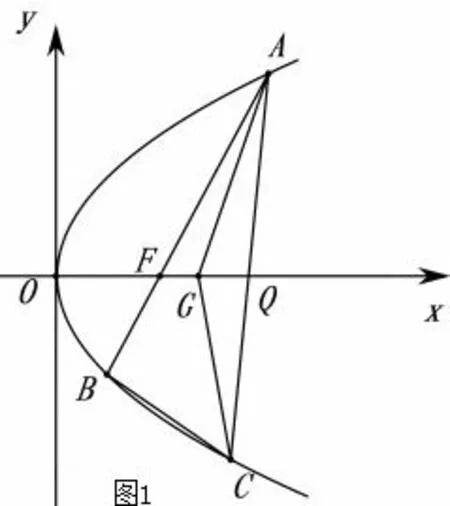
图1

试题分析题目结构清晰，知识方面主要考查抛物线的有关定义与基础知识，直线方程，直线与抛物线的位置关系，重心性质，三角形的面积，均值不等式等;思想方面主要考查转化与化归，数形结合等思想.综合考查考生逻辑思维、推理论证及运算求解等方面的能力，试题的思维过程和运算过程体现了能力立意的命题思想，较好地体现了对直线与圆锥曲线的核心内容和基本思想方法的考查.

由于问题(1)较为简单，本文不作讨论，下面只对问题(2)进行探究.

二、解法探析

解法一(官方答案)(1)由题意得即p=2.所以，抛物线的准线方程为x=-1.

(2)由(1)可得抛物线的方程为y2=4x，设A(xA,yA)，B(xB,yB)，C(xC,yC)，G(xG,yG).令yA=2t，t0，则xA=t2.由于直线AB过F，故直线AB方程为代入y2=4x，得故2tyB=-4，即所以又由于xG=及重心G在x轴上，故得所以，直线AC方程为y-2t=得由于Q在点F右侧，故t2＞2，从而

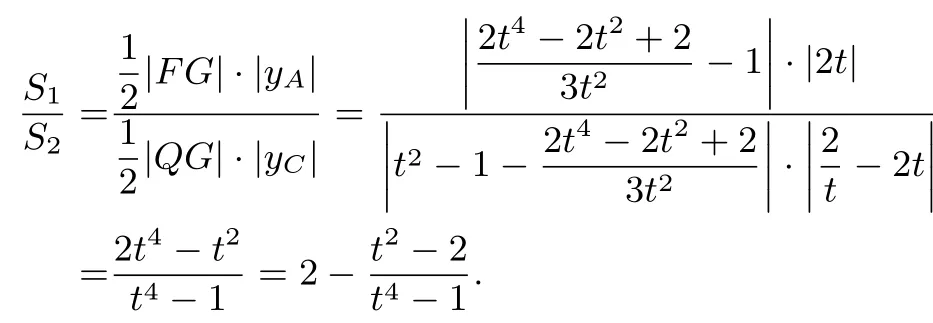
令m=t2-2，则m＞0，

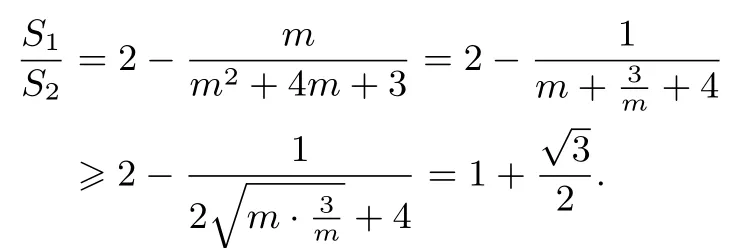
评注本解法是通过联立方程组，得到一元二次方程，利用韦达定理求得各点的坐标，从而得到面积比的表达式，换元后利用均值不等式得出答案.此方法本运算量虽大，但方法是通性通法，是解决直线与圆锥曲线相关问题的最常用手段.所以在平时的教学中要注重一般性的解题规律和方法，要重视知识的生成过程，尽量创设问题情境引导学生探究知识，培养学生分析问题、解决问题的能力.

解法二(以点为参数)

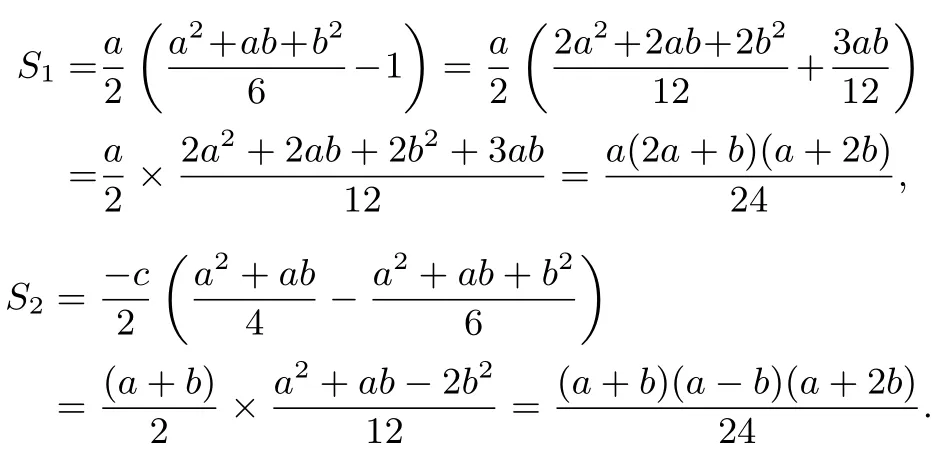
所以

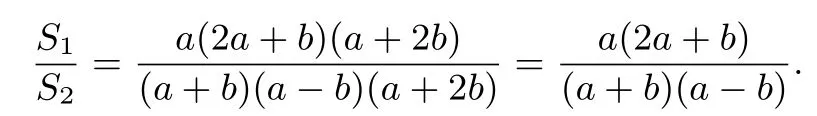
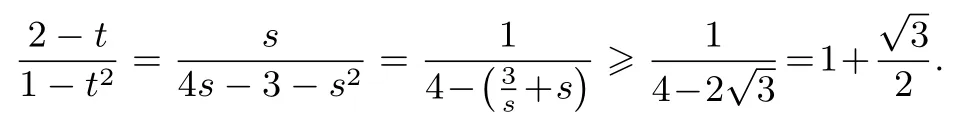
评注在处理抛物线有关问题时，直接用点的坐标作为变量也是一种较为常用的方法，这是由抛物线的特点决定的：用其中一个坐标能比较容易表示另一个坐标.本解法的好处是不用联立方程组，在面积作比时消去了一项，从而得到一个二次比二次的式子，既可以换元用均值不等式求最值，也可以用导数求最值，比解法一的运算量要少.

以上的两种解法，从不同的角度出发思考问题，各显神通.这充分体现数学高考题的不拘一格，一道试题往往考查多种能力、多种思想方法;同时，高考试题在命制时充分考虑到考生数学能力的个体差异，多数试题的解答方法、思维方式不是唯一，一题多解，给考生提供了较大的发挥空间.这样通过方法的选择、解题时间的长短，甄别出考生能力的差异，达到精确区分考生的目的.另外也说明高考要突出考查知识主干，贴切教学实际，重视数学的基本能力与思想方法，所以我们要在平时的学习与训练中重视知识的储备和方法的积累，才有可能缩短思维的长度，达到事半功倍的效果.

三、结论推广

数学家波利亚曾说：“解题就象采蘑菇一样，当我们发现一个蘑菇时，它的周围可能有一个蘑菇圈.”解答完本题后，思考：试题的问题(2)中，取得最小值的这个结论能否在抛物线中一般化?解答方法是否依然有效?经进一步的探究，可得如下结论：

结论1如图1，已知抛物线Γ:y2=2px(p＞0)的焦点是F，过点F的直线交抛物线于A,B两点，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且Q在点F右侧.记△AFG,△CQG的面积分别为S1,S2.则的最小值为

结论2如图1，已知抛物线Γ:y2=2px(p＞0)，过点F(f,0)(f＞0)的直线交抛物线于A,B两点，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且Q在点F右侧.记△AFG,△CQG的面积分别为S1,S2.则的最小值为

由于结论2比结论1更具一般性，下面只给出结论2的解答.

结论2的证明设G(g,0)，Q(q,0).则由A,F,B共线，得kAB=kAF，即化简得ab=-2pf.同理，由A,Q,C共线，可得ac=-2pq.因为△ABC的重心G，于是即得c=-a-b，g=其中a＞0＞b.故

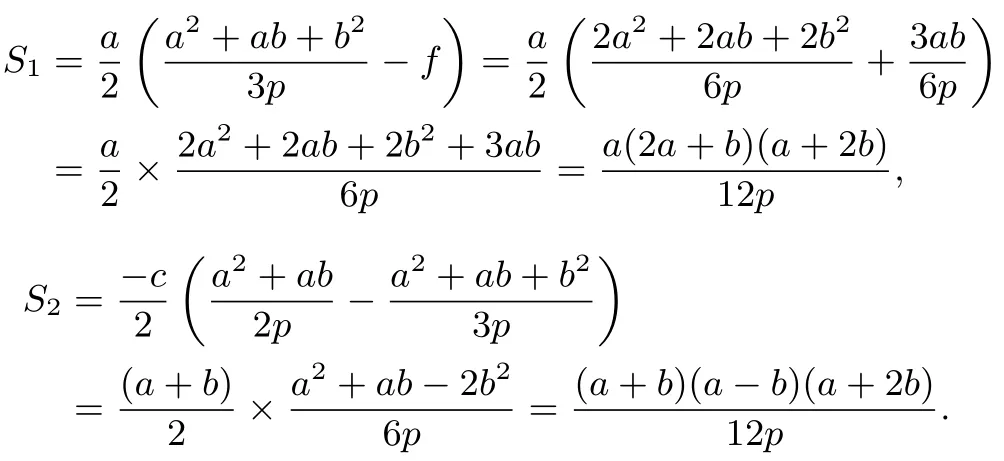
四、试题的衍生性质

结论3如图1，已知抛物线Γ:y2=2px(p＞0)，过点F(f,0)(f＞0)的直线交抛物线于A,B两点，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且Q在点F右侧.记△AFG,△CQG的面积分别为S1,S2，当取得最小值时，有CG⊥x轴.

结论3的证明由结论2的解答，可知当时令取得最小值此时即于是联立

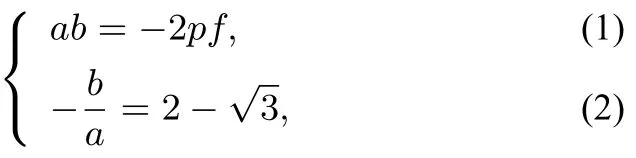
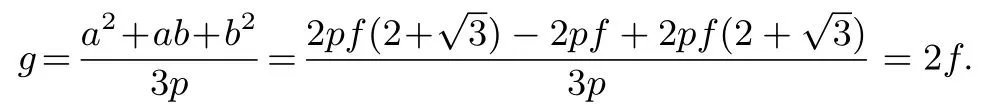
由于c=-a-b，得

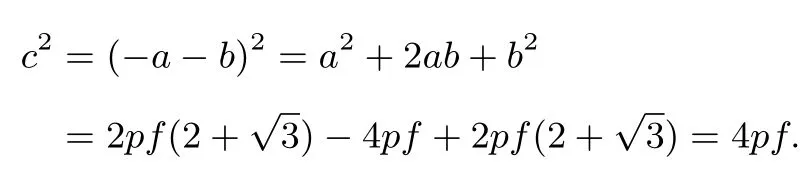
五、试题的本质探索

通过试题与试题的推广，再进一步思考：圆锥曲线一般有着类似的性质，这体现圆锥曲线性质的内在统一的和谐美，那么椭圆与双曲线是不是也具有类似结论1与结论2的性质?

答案是肯定的，而且还可以得到更一般的结论：

结论4如图2，在△ABC中，若G是△ABC的重心，过点G作直线交AB于点F(F与点A,B不重合)，交AC于点Q(Q与点A,C不重合)，记△AFG,△CQG的面积分别为S1,S2.则的最小值为

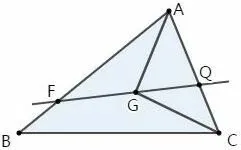
图2

结论4的简解因为G是△ABC的重心，所以设则由于F,G,Q共线，故即λ+µ=3(0＜µ＜3).因为有又因直线AG经过边BC的中点，易得S△ABG=S△ACG.所以

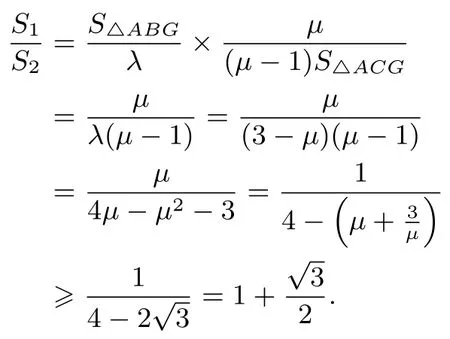
评注可以看出，结论4是试题的命题本质，高考试题将这个本质放在圆锥曲线中，赋予更丰富的图形与知识，进行考查直线与圆锥曲线的相关内容，考查学生的转化与化归，数形结合等思想与能力.

事实上，解析几何问题的本质仍是几何问题，解题时“莫为浮云遮望眼”，要善于“拨开迷雾”寻找“真颜”，充分把握解析几何中图形的特征，紧扣其中关键的几何要素，挖掘图形相应的几何性质，恰当地运用平面几何的相关知识，将解析法与平面几何方法相结合，往往能简化运算，优化解题过程，能起到四两拨千斤的功效.

六、解题反思

数学教育家波利亚曾说：与其穷于应付繁琐的数学内容和过量的题目，还不如适当选择某些有意义的题目去帮助学生发掘题目的各个方面，在指导学生解题的过程中，提高他们的才智与推理能力.学数学离不开解题，但不能仅仅局限于老师讲题、学生做题.教师在教学过程中要重视“研究”，要有数学研究的实践与体验，以研究者的思维与逻辑组织教学，讲解一道题不仅仅局限于这个问题本身，而是能借助这道题的背景，将研究的问题引向深入，探索隐藏在题目背后的奥秘，挖掘题目的真正内涵，能够找到解决这个问题与解决其它问题在思维上的共性.这样我们才能领会到试题命制的深刻背景，才能引领学生跳出题海，真正做到触类旁通，举一反三.

高考试题是精心之作，每年的高考题在命题角度、题型、难度等方面都进行了充分考虑，是知识、能力和思想方法的载体，是命题思想、命题理念的程序化展现，具有典型性、示范性和权威性.除了具有测试与选拔功能外，还具有良好的教学功能，要了解高考动向、把握高考脉搏，高考试题的研究分析是重要的路径.所以我们教师对要对高考试题做深入的分析与研究，教师要跳入题海多做题多思考，才能做到融会贯通、信手拈来，帮助学生跳出题海.对高考试题的深度探究，不仅使教师清晰地理解命题人的思想、命题背景和考查目的，还可以更好地培养学生思维品质，提高学生提出问题、分析问题和解决问题的能力，提高学生的数学核心素养.