探析2019年北京卷理科解析几何压轴试题*

福建省龙海第一中学新校区(363100) 苏艺伟

一、试题呈现

题目(2019年高考北京卷理科)已知抛物线C:x2=-2py经过点(2,-1).

(1)求抛物线C的方程及其准线方程.

图1

(2)设O为原点，过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M,N，直线y=-1分别交直线OM,ON于点A和点B.求证：以AB为直径的圆经过y轴上的两个定点.

二、试题评析

本题以直线和抛物线为载体，考查求抛物线的方程，准线以及证明圆过定点.试题背景朴实，亲切，容易入手，分层递进，步步得分.试题第二步突出了对圆锥曲线中定点问题的考查，不回避热点问题，能够让考生学有所用，学有所得.第二步看似简单，实则具有一定的探究意义，能够考查学生的推理能力和数学运算能力，既体现了数学本质，彰显了对数学核心素养的考查要求，又让人感受到了命题者的独具匠心.

三、试题解析

如图1所示，设抛物线焦点F(0,-1)，准线方程为y=-1.设直线l方程为y=kx-1(k0).代入x2=-4y得x2+4kx-4=0.设M(x1,y1)，N(x2,y2).则x1+x2=-4k，x1x2=-4.故y1y2=1，x1y2+y1x2=x1(kx2-1)+(kx1-1)x2=-4k.

法1由于题目已经提示以AB为直径的圆经过y轴上的两个定点，故可设定点坐标为D(0,n)，借助--→DA·--→DB=0这个关系求出n，从而得到定点坐标.

法2先求出以AB为直径的圆方程，再结合题目提示定点在y轴上解出定点坐标.

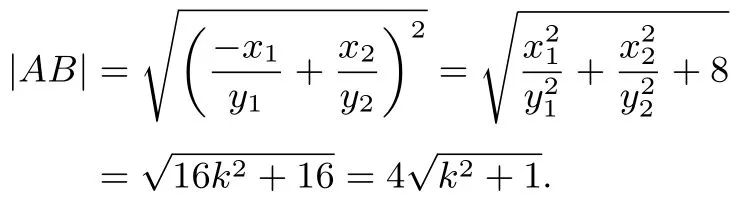
法3考虑两种特殊的情况，得到两个特殊的圆，发现都过点(0,1)和(0,-3)，再证明这两个点就是符合题意的定点.

假设直线l斜率为0，此时以AB为直径的圆方程为x2+(y+1)2=4，过点(0,1)和(0,-3).假设直线l斜率为1，此时以AB为直径的圆方程为(x-2)2+(y+1)2=8，过点(0,1)和(0,-3).所以以AB为直径的圆经过y轴上的两个定点(0,1)和(0,-3).下面证明之.

通过上述分析，不难发现第二问是典型的证明定点问题，思路一般有如下几种：

第一种：采用假设存在验证法，先假设存在定点，然后建立等量关系，若能求出相应的量，就说明存在，否则就不存在.

第二种：相关几何量用曲线系里的参变量表示，再证明结论与特定状态或与参数无关;

第三种：先把相关变元特殊化，在特例中求出定点，再证明符合题意;

四、试题探究

思考1如果改成证明以AB为直径的圆经过定点，如何证明?

法1设D(x0,y0)，则故

化简得

即

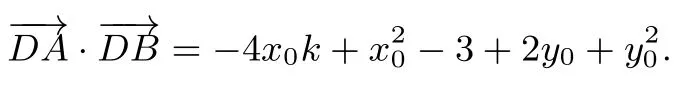
法2设AB中点为T，则故T(2k,-1).

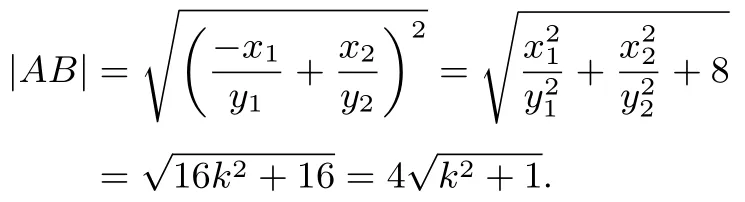
思考2通过上述分析，不难发现以AB为直径的圆经过的两个定点(0,1)和(0,-3)，抛物线的焦点恰好是其中点.也就是说可以把本题推广到一般情况吗?

结论已知抛物线C:x2=-2py，设O为原点，过抛物线C的的焦点作斜率不为0的直线l交抛物线C于两点M,N，直线分别交直线OM,ON于点A和点B.则以AB为直径的圆经过y轴上的两个定点，这两个定点的中点是抛物线的焦点.

下面借助Geogebra软件验证：

第一步：利用工具栏中的滑动条构造一个变量p;

第二步：在输入框中输入xˆ2=-2py，作出抛物线x2=-2py.在输入框中分别输入F=(0，-p/2)和y=p/2，作出焦点和准线;

第三步：利用工具栏中的直线按钮构造出过焦点的一条直线，与抛物线交于点M,N;再分别作出直线OM,ON，交准线于A,B两点;

第四步：利用工具栏中的中点工具作出AB中点T，再利用工具栏中的圆按钮构造出以AB为直径的圆;

第五步：拖动第三步中构造出的直线上的点G，观察发现当直线绕着焦点转动时，动圆恒过y轴上的两个定点且以焦点为中点.如图2所示.

图2

五、试题变式

变式1椭圆过点且斜率为k的动直线l交椭圆于A,B两点.是否存在定点M，使得以AB为直径的圆恒过点M?若存在，求出点M的坐标;若不存在，说明理由.

解析若直线l斜率不存在，则以AB为直径的圆与y轴的交点为M1(0,1)，M2(0,-1).若直线l斜率为0，则以AB为直径的圆与y轴的交点为所以符合条件的点是M(0,1).下证M(0,1)就是满足条件的点.

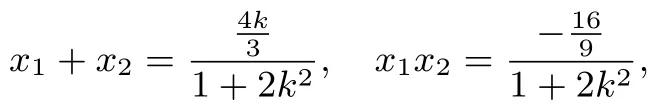
变式2椭圆的左焦点为F1，右焦点为F2，离心率过F1的直线交椭圆于A,B两点，且△ABF2的周长为8.

(1)求椭圆E的方程;

(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P，且与直线x=4相交于点Q.试探究：在坐标平面内是否存在定点M，使得以PQ为直径的圆恒过点M?若存在，求出点M的坐标;若不存在，说明理由.

解析根据题目条件易求得椭圆E的方程为1.由得(4k2+3)x2+8kmx+4m2-12=0.令Δ=0，得4k2-m2+3=0.设P(x0,y0)，则x0=故由得Q(4,4k+m).取得以PQ为直径的圆方程为(x-2)2+与x轴的交点为M1(1,0),M2(3,0).取得Q(4,0)，以PQ为直径的圆方程为与x轴的交点为M3(1,0),M4(4,0).所以符合条件的点是M(1,0).下证M(1,0)就是满足条件的点.因为从而即因此以PQ为直径的圆恒过点M.