非中心奇异Wishart分布的特征函数
李 斐,李 琴
(烟台大学数学与信息科学学院, 山东 烟台 264005)
文献[1-2]中讨论了非奇异多元正态矩阵和非奇异Wishart矩阵的密度函数、特征函数以及其他一些重要性质.UHLIG[3]将Wishart分布推广到了奇异的情况,给出了奇异Wishart分布的密度函数等.DIAZ-GARCIA等在文献[4]中进一步推广和完善了UHLIG的结果,给出了更一般情况下的奇异Wishart分布的密度函数.更多的相关结果可以参阅文献[5-7].
文献[1-2]给出了非奇异的Wishart矩阵的特征函数,其中文献[2]也给出了非奇异非中心的Wishart矩阵的特征函数.但是对于最复杂的奇异非中心Wishart分布的特征函数并没有讨论.本文不但给出了奇异非中心Wishart分布的特征函数,还将Wishart分布的一个重要性质推广到了奇异非中心的情况下,并用特征函数加以证明.
1 奇异非中心Wishart分布的特征函数
由文献[2]中矩阵正态分布的定义,易知若Yr×s~N(O,Is×s,Ir×r),即vec(Y′)~Nrs(O,Ir×r⊗Is×s).令
X=M+AYB′,
其中An×r,Bm×s为列满秩矩阵.则不难得到
vec(X′)=vec(M′)+A⊗Bvec(Y′)~Nmn(vec(M′),AA′⊗BB′),
即X~Nn×m(M,Σ,Θ).其中Θ=AA′,Σ=BB′,rank(Σ)=s,rank(Θ)=r.当Σ,Θ为奇异矩阵时,称X服从奇异的正态分布.
文献[3]将Wishart分布推广到了n 定义1 若X~Nn×m(M,Σ,Θ),其中rank(Σ)=s,rank(Θ)=r.令 S=X′Θ-X, 则S服从奇异非中心Wishart分布,记为 其中Ω=Σ-M′Θ-M,q=min(r,s). 下述定理给出了S的特征函数. Σ-M′Θ-M,l=min(r,s).则S的特征函数为 (1) 即为 (2) 证明 对Σ,Θ做特征值分解如下, 其中DΘ,DΣ分别为r×r,s×s阶的对角矩阵,对角元素为Θ,Σ的非零特征值.P,Q分别为n×n,m×m阶的正交矩阵. 令 (3) 注意到Z为奇异正态分布,根据文献[2]的定理2.1可以得到Z的密度函数表达式以及下式, (4) 因为 采用文献[1]中对Wishart分布矩阵的特征函数的定义,注意到z1,…,zr相互独立,有 (5) (6) (7) 再令 (8) (9) 将式(7),式(8)代入式(6)中,可得, (10) 易知式(10)的前两部分相互独立,第三部分几乎处处为常数,将式(10)代入式(5)可得, (11) 分别计算式(11)中的2个期望,对于第一个期望化简如下,因为 (12) 其中非中心参数 (13) 由非中心卡方分布的特征函数,式(12)可进一步整理, (14) 计算式(11)中的第二个期望, (15) (16) 由式(9)得 以及式(3),将式(16)的第一个指数函数的指数部分化简如下, (17) 式(16)的第二个指数函数的指数部分化简如下, (18) 式(16)的第三个指数函数的指数部分化简如下, (19) 式(16)的第四个指数函数的指数部分化简如下, (20) 将式(17)—(20)代入式(16)可得式(1),进一步化简为式(2),故定理得证. 当M=0时,S即为中心的奇异Wishart分布,由定理2可得其特征函数. 当rank(Σ)=m时,即Σ为非奇异矩阵,由定理2可得其特征函数. 推论4的结论与文献[3]中的相关结果是一致的. 我们将文献[1]的定理3.2.5推广到奇异非中心的情况下,并利用定理2进行证明. (21) 证明 分以下3种情况讨论: (1) 当A为p×p阶正交矩阵时,由定理1, 故式(21)成立. 故式(21)成立. (3) 因为p×m阶的矩阵A可进行奇异值分解, 其中U,V均为正交矩阵,则利用(1),(2)的结论,定理可证.


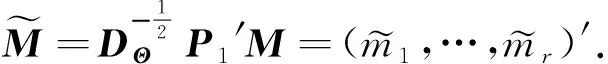
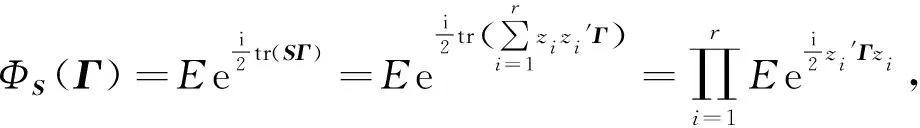
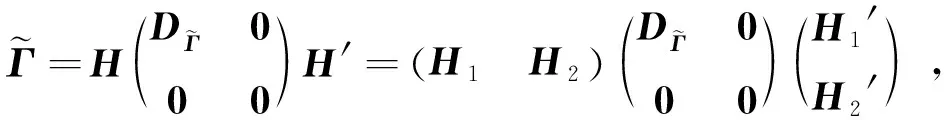
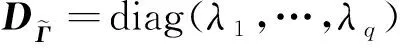


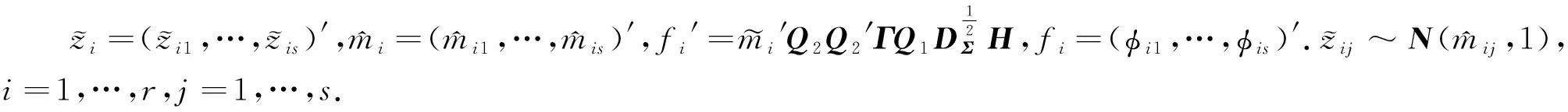

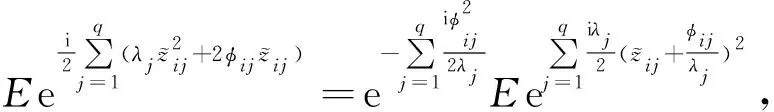

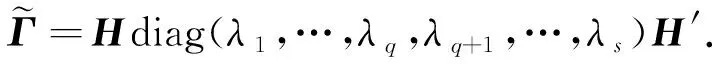


2 应 用