“直观想象”在求解函数题中的渗透与启示
山东
《普通高中数学课程标准》中强调:突出数学素养,在数学课程逐渐展开的过程中,促进学生数学核心素养的形成和发展.“直观想象”是六大数学核心素养之一,是发现和提出问题、分析和解决问题的重要手段,主要表现为:建立形与数的联系,利用几何图形描述问题,借助几何直观理解问题,运用空间想象认识事物.一提到“直观想象”,人们往往先想到的是立体几何和解析几何问题,殊不知,“直观想象”的渗透颇为广泛,在许多代数问题尤其是函数问题中也体现得淋漓尽致!
由于函数在整个高中数学中具有举足轻重的地位,因而在高考或各地模拟考试的压轴小题中频繁出现与函数相关联的导数、方程及不等式的一类问题,起到了“一夫当关,万夫莫开”的把关定向作用.这类问题不仅能很好地考查函数、方程、不等式和导数的有关知识以及换元、构造、对应、配凑等意识及知识的综合运用能力,而且适时地构造函数,利用函数的图象使问题的解决明朗化,也是培养和形成“直观想象”数学核心素养的良好载体.本文将对实例(主要是教学考试杂志社原创研发试题)进行剖析,力求揭示“直观想象”在求解函数压轴小题这类试题中的渗透,探索它们的题型规律,以期望在三轮复习的冲刺阶段为教师指导学生复习做出参考.
一、函数零点(方程的根)个数的判断
例1.已知关于x的方程(ex-1)2-|ex-1|+k=0,当k∈R,方程实数根的个数可能是
( )
A.3 B.4
C.6 D.8
解析:由题意,设t=|ex-1|(t≥0),则方程可化为t2-t+k=0①,做出函数y=|ex-1|的图象.
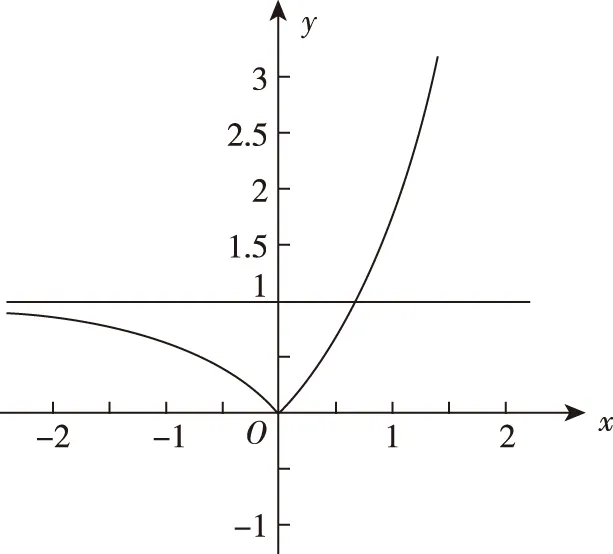
结合图象可知,当t=0或t≥1时,方程有一个实数根,当t<0时,方程无实数根,0 所以,对于①, 当k=0时,①有两个根,分别是t=0,t=1,则方程|ex-1|=0,x=ln1=0,|ex-1|=1,x=ln2,共2个实数根; 当k<0时,①有一正根一负根,并且正根大于1,当|ex-1|=负根无意义,当|ex-1|=正根时,方程有两个实数根,综上,故选B. 点评:本题是含有绝对值的方程根的个数判断问题,在换元后将原方程转化为新元的一元二次方程的基础上,构造绝对值函数(分段函数),结合函数的图象分类讨论做出判断的,很好地考查了函数与方程、函数图象、绝对值函数的性质的运用.结合图象直观合理地分情况讨论是解题的关键. 例2.已知函数g(x)=8e[ln(x+1)]2-(2e+8)(x+1)·|ln(x+1)|,f(x)=-2x2,则方程g(x)-f(x+1)=0的实数根的个数为 ( ) A.4 B.5 C.6 D.7 解析:因为方程g(x)-f(x+1)=0,所以 8e[ln(x+1)]2-(2e+8)(x+1)|ln(x+1)|+2(x+1)2=0. 点评:本题以方程的根的个数判断为背景,考查了方程与函数的转化、换元、导数在研究函数的单调性中的应用等知识,最后结合图象做出判断,很好地考查了直观想象、数学运算和逻辑推理等数学核心素养. ( ) A.e B.1-m C.1+m D.1 点评:本题依据目标式的结构特征,换元转化为新元的一元二次方程后利用韦达定理,并结合导函数与原函数的单调性的关系,做出图象后整体求解.很好地考查了换元转化、整体处理的意识和直观想象、逻辑推理等核心素养的运用. ( ) A.a-1 B.1-a C.-1 D.1 点评:本题是例3的姊妹题,是将例3基于指数式形式的呈现转换为了对数式形式的呈现,其解答思路与例3如出一辙,换元转化为新元的一元二次方程后利用韦达定理,并结合导函数与原函数的单调性的关系,做出图象后整体求解.其中结合函数求解,很好地体现了“直观想象”数学核心素养的渗透. ( ) 点评:本题以新定义运算为背景,构造函数,在利用导数分析函数性质和变化趋势的基础上,做出图象,结合图象求解,很好地体现了“直观想象”数学素养的渗透应用. 点评:解决此类问题往往将问题转化为方程根的问题,再转化为两函数图象的交点问题.本题主要考查函数与导数的综合应用以及直观想象的数学核心素养. 解析:因为函数f(x)=x2+e4x-2m(x+2e2x)+5m2,所以f(x)=(x-m)2+(e2x-2m)2,可表示两动点P(x,e2x),Q(m,2m)距离的平方. 点评:本题充分挖掘函数式所蕴含的几何背景,将不等式成立转化为最值问题,进而构造函数,利用导数的几何意义求解,充分体现“直观想象”数学核心素养的渗透. ( ) 点评:本题基于高考的函数与导数的综合应用考查转化能力、计算能力以及数形结合思想,在分类讨论的基础上结合图象进行求解,很好地考查了直观想象、逻辑推理和数学运算等数学核心素养. 1.数学核心素养是相对于其他素养而言的,是专指一个人在处理事情的过程中体现出的数学方面的素质与水平的高低,或者是情境中某些因素激发了个人关于数学的认知结构,从而使得个人更多地从数学角度来看待问题.近几年高考命题的趋势表现在对数学核心素养的考查越来越多、越来越明显,高考中渗透和强化对数学核心素养的考查是近年高考命题的一大趋势.因此,在高考复习备考的冲刺阶段,无论是对高考命题规律的分析和趋势的预测,还是对热点题型的分析,都不能忽视对核心素养的考查.关注核心素养考查的变化趋势,也就是关注高考的命题趋势.

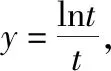
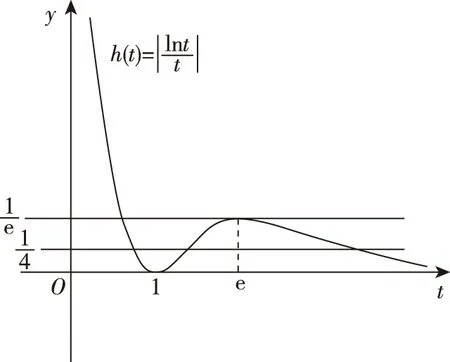
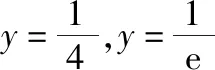
二、函数方程中关系式的求值问题
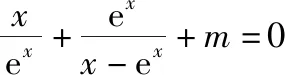
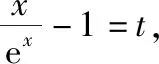
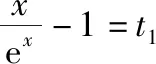
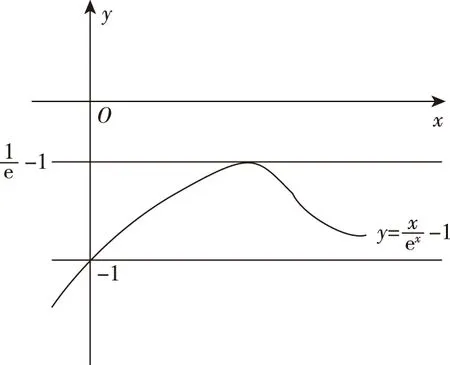
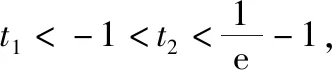
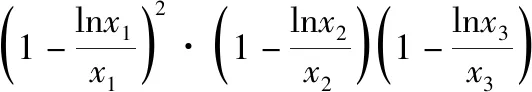
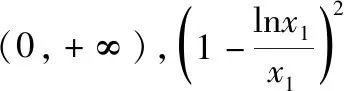
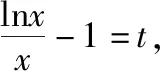
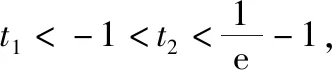
三、函数方程中参数范围的确定
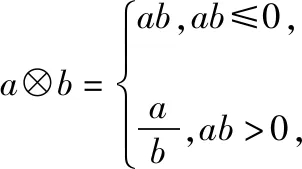
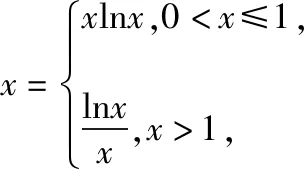
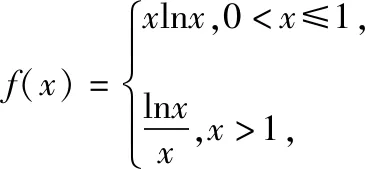
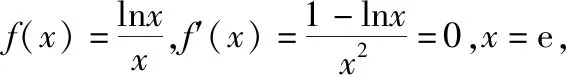
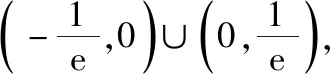
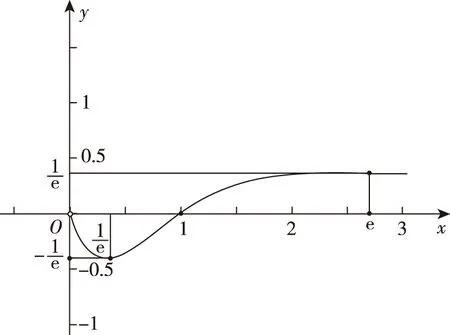
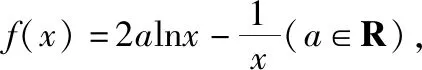
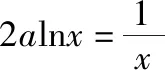
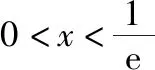
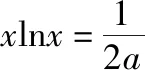
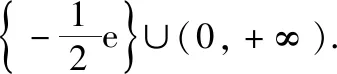
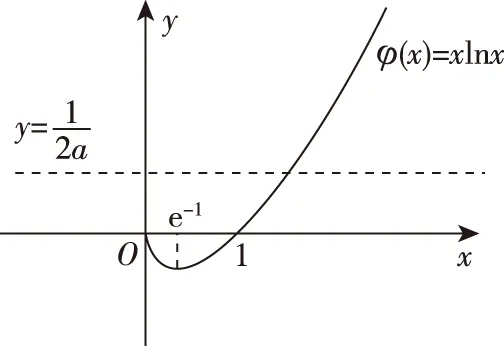
四、函数不等式中参数范围的确定
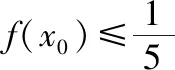
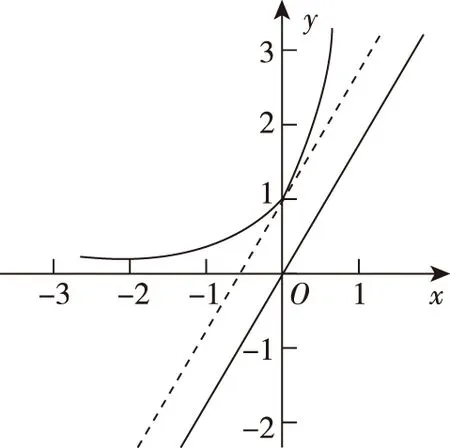
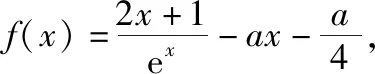
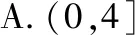
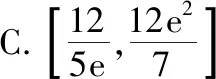
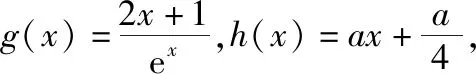
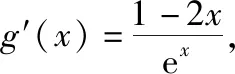
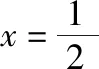
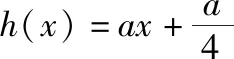
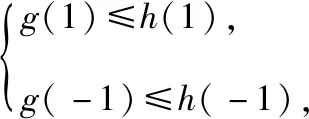
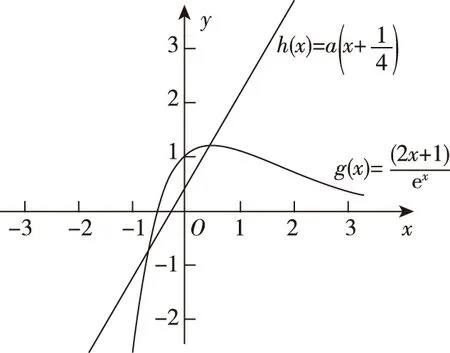
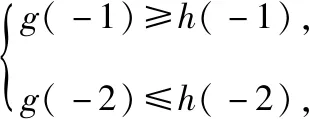
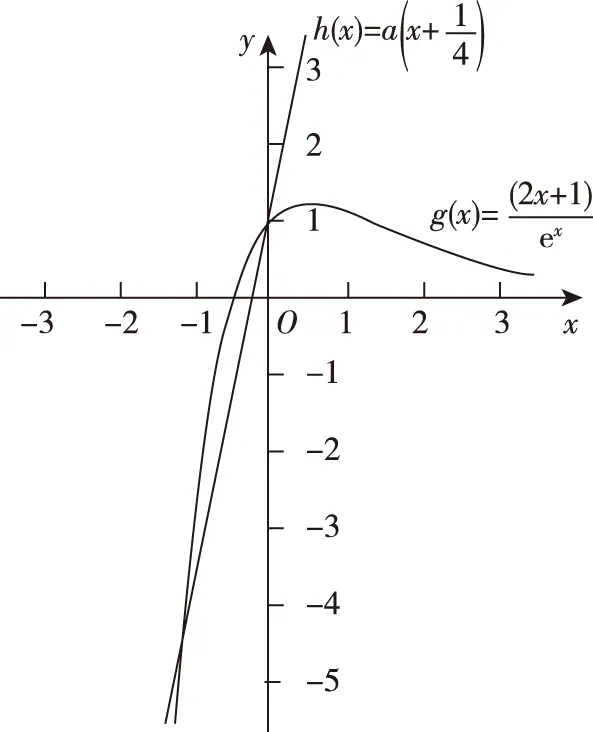
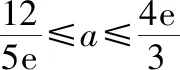
启示感悟


