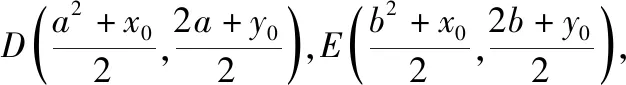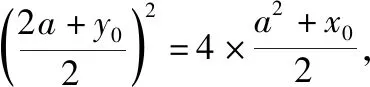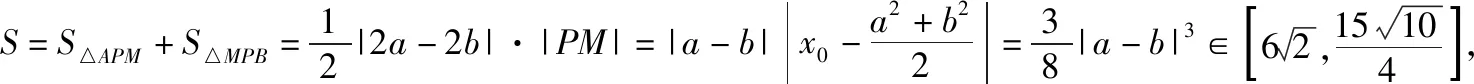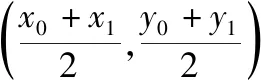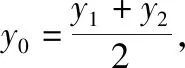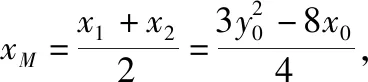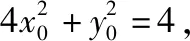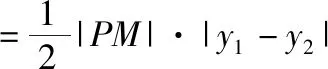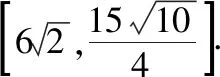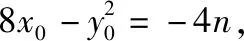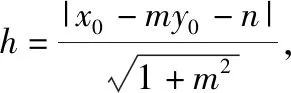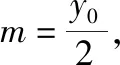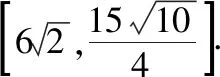依纲托本 深研典例
——浅谈2019年浙江省高考数学复习策略
浙江
《普通高等学校招生全国统一考试大纲的说明》(以下简称《考试说明》)制定有比《普通高等学校招生全国统一考试大纲》(以下简称《考试大纲》)更为具体的考试内容,是高考命题的准绳,也是我们复习备考的依据,关系到当年数学高考“考什么”“怎么考”“有多难”等重要问题.
一、说明解读:稳字当头,保持特色
2019年浙江省高考数学《考试说明》的“考试性质与对象”“考核要求”“考核内容及要求”“考试形式及试卷结构”以及“题型示例”与2018年相比较,字词上没有任何调整变化,这预示着浙江省高考数学试题将继续保持稳定,突出基础性、多层次,重视通性通法,淡化特殊技巧,重思维、重本质,强调问题性,凸显数学素养等浙派特色,以适应社会发展对多样化高素质人才的需要.
二、考点分析:继承传统,预测变化
由于《考试说明》中“知识要求”的三个层次(了解、理解、掌握)、“能力要求”(逻辑思维能力、空间想象能力、运算求解能力、数据处理能力、综合应用能力)和“考查内容及要求”都一字未动,这启示2019年浙江省高考数学卷仍会坚持减缓坡度,增加层次,考点不变,多题把关,重点考查三角函数、立体几何、数列、解析几何、函数与导数等主干知识.三角函数题,不排除三角函数的性质与解三角形交汇命题,命题者以三角函数的恒等变形与性质为出发点,融合求解三角形的某元素或三角形的面积的最值;数列题基本会以等差与等比数列交叉命题为主,但可能融入构造新的数列的通项与前n项和的求解及不等式证明;立体几何题仍以棱锥或棱柱为载体,考查平行、垂直以及夹角或体积的计算;解析几何题以圆锥曲线为背景求解,以图形中某些量的范围和最值的求解为主要目标,考查解析几何的基本思想方法和数学运算素养;函数与导数题以基本概念、含参不等式或特殊不等式为目标,考查数学抽象、逻辑推理等核心素养.
同时在客观题中会进一步贯彻“文科的韵味,理科的深度”的命题特色,知识上覆盖集合、复数、三视图、随机变量的期望与方差、空间角、二项式定理、线性规划、向量等内容,并且在考查基础知识、基本技能掌握程度的同时,兼顾试题的基础性、综合性和应用性,低档题会送分到位,注重对数学思想方法、数学本质的理解水平的考查,高档题则思维难度较大,展现数学的科学价值和人文价值.由于试题需要展现“必备知识、关键能力、学科素养、核心价值”的层次与关系,解答题可能存在两个“微调”:顺序的调整,设问方式的调整.
2018届部分考生过度按2017年浙江卷数列与不等式压轴进行模拟,而2018年试题降低了数列题的难度,将函数与导数设计为压轴题,按理说全卷难度下降,但很多学生在心理上却有强烈的不适应,失分严重.
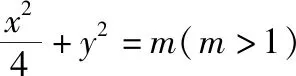
通常考查基本不等式的应用时要求求出最值,此题明显体现出设问方式迂回为作答取最值时的取等条件.
解析1设点A(x1,y1),B(x2,y2).显然,当直线AB的斜率为0时,P为弦AB的中点,故可设直线AB的方程为x=t(y-1),代入椭圆方程得(t2+4)x2+8tx+4t2(1-m)=0,
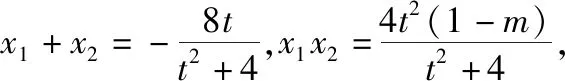
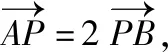
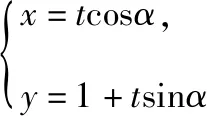
又t1=-2t2,则由基本不等式,得点B横坐标的绝对值
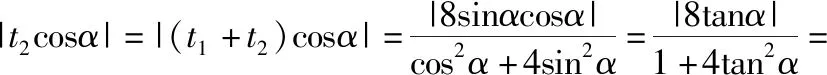
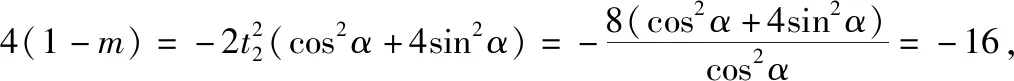
所以当m=5时,点B横坐标的绝对值最大为2.
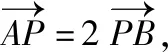
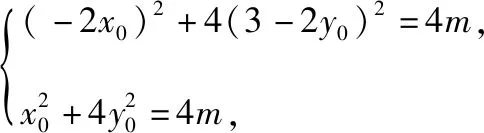
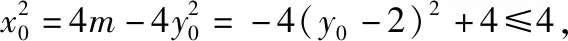
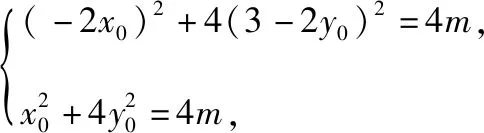
解析1应用直线与圆锥曲线的位置关系进行硬解——联立方程,应用韦达定理建立函数模型求解,但有“小题大做”的不适感;解析2注意到问题研究相似椭圆(离心率相等的椭圆)背景下的线段比例的问题,因而利用直线的参数方程表示对应线段的长度关系;而解析3和解析4则灵活运用向量的坐标表示,利用点在曲线上消元直指目标,特别是解析4,从整体上发现动点的轨迹,显得高明简洁.这正是多向思维给我们带来的益处——直接硬解虽够劲,不惧迂回有智慧,巧引点差有深度,整体透视显功底.
三、备考建议:倡导回归,多些研究
1.回归课本,重视基础知识复习
回归课本是老生常谈的话题,但教材是我们学习的最主要资源,是数学知识内容与能力素养的最重要载体.回归课本,重读教材,对《考试说明》要求的概念、公式和方法进行去粗取精的提炼加工,使数学知识网络化、系统化;回归课本,加强对数学核心概念的整体理解,可以促发自己对知识与能力的再生性生长,由表及里地纵横联系,引发不同的感觉、迥异的理解和更广的视野,便于记忆提取和应用.回归课本也要能“出乎其外”,归纳整合章节知识,形成专题知识或专题材料,切忌只见树木,不见森林,头脑中存在的只是课本知识的“原生态”.如角的复习,可这样归纳:共面直线所成的角→异面直线所成的角→直线和平面所成的角→二面角,从而弄清“角”的形成与发展,使概念更加准确清晰.又如数列这一章,既要掌握基本数列(等差、等比数列)的通项公式、求和公式,也要理解其定义与性质,还要总结其求通项、求和方法中重点体现的构造转化思想.
浙江省高考数学一向注重考查数学基本概念、基础知识,绝大部分试题面向全体考生,《考试说明》强调的考点都在教材内,表明课本是试题“万变之宗”.2018年浙江卷很多问题设计取材于课本,第1题考查集合的基本运算,第2题考查双曲线的简单几何性质,第4题考查复数的运算与共轭复数的定义,第5题考查函数的奇偶性及函数的零点,第6题考查空间中直线与直线以及直线与平面的位置关系的性质与判定,这些试题需要考生有针对性地调动基础知识进行分析;试题的第12~14,18题等由课本中的例、习题延伸改造而来,充分体现了“回归课本”必要性.
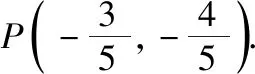
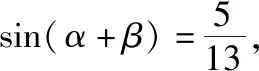
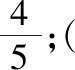
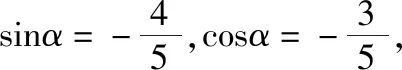
2.注重研究,积累基本活动经验
高考数学试题“源于课本,高于课本”,一直注重在继承传统的同时不断进行创新,每年都会出现一些令人耳目一新的试题,这类题有较大的自由度与思维空间,体现自主学习与主动探究精神.作为高三学生,对高中数学知识的研究会比高一高二时更灵活、思考更深入、探究更全面,因此“回归课本”,学会从课本中深入挖掘知识,揭示问题的本质,学会从更高的层次研究教材,对知识点进行思维深加工,创造性地解决问题,则会深切地认识到课本是个取之不尽,用之不竭的“库”,难题偏题“无尽藏也”,从而在考场上“以不变应万变”,应对自如.
例3(2018·浙江卷·8)已知四棱锥S-ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点),设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S-AB-C的平面角为θ3,则
( )
A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1
C.θ1≤θ3≤θ2D.θ2≤θ3≤θ1
答案:D.
此题比较空间角大小的通法是回到定义,作出角θ1,θ2,θ3,再利用解三角形的知识解题,如图所示;或建立空间直角坐标系,以向量为工具求解.如果我们复习过程中多些研究的眼光,可以深入地揭示空间角的本质规律,“面面角”是“线面角”中的最大角,“线面角”是“线线角”中的最小角,则可一望而解.

一些创新题隐藏其背景,给我们一个思维充分自由驰骋的空间来探究其中的数量关系,在思维上具有一定的开放度,在探究结论上又具有一定的收敛性.
例4(2018·浙江卷·10)已知a1,a2,a3,a4成等比数列,且a1+a2+a3+a4=ln(a1+a2+a3),若a1>1,则
( )
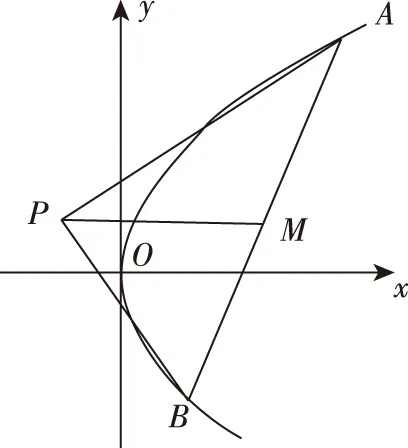
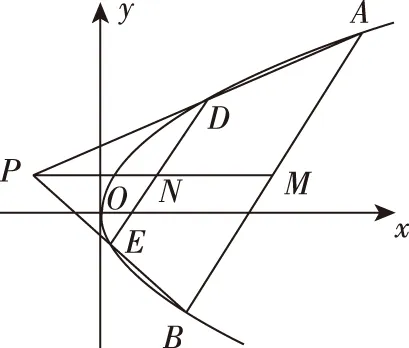
A.a1 C.a1 答案:B. 布鲁纳指出:“问题常常作为一种标准,决定着学生素质的现状以及他们理解的程度……从一定意义上说,问题是通向理解之途.”为此我们常简单地认为数学是“做”出来的,因而,高考复习数学的主旋律是“题”.实际上,“刷题万道,不如精做一道”,为了在“做数学”的过程中,获得数学基本活动经验,复习题应该“少而精致,锲而不舍”,进而获得活动过程中产生的数学基础知识、基本技能和基本思想,“少”来自教师角度,教师应根据学生情况针对性精选问题,去掉重复性的、已会的,补充体现重要思想方法与知识的联系的题和有研究价值、能提升数学素养的题,这比单纯“刷题”更高效;“精致”于学生而言,要求学会引申反思,融会贯通,举一反三,有一题多解、多题一解的思考习惯;“锲”从学生角度,需遇到难题不轻言放弃,肯用心钻研,善于利用同伴资源,群策群力,共同解决问题,直至对问题豁然开朗. 例5(2018·浙江卷·21)如图,已知点P是y轴左侧(不含y轴)一点,抛物线C:y2=4x上存在不同的两点A,B满足PA,PB的中点均在C上. (Ⅰ)设AB中点为M,证明:PM垂直于y轴; ①②两式相减,得a+b+y0=2(a+b),即y0=a+b,又M为AB的中点,则点P,M的纵坐标相等,同在直线y=a+b上,所以PM⊥y轴. 解题之后,我们一定要认真地回顾自己的思路,反思解题中的得与失:题(Ⅰ)可以通过设点,利用“点差法”建立起弦AB的端点与点P的联系,巧妙利用点的坐标表示与位置关系上的对称性,从而获得结论,其好处是通过形的直观,使运算简洁,更重要的是避免字母运算上的抽象繁琐;也可以通过设直线,结合平面几何知识推算出MN为一条水平直线.题(Ⅱ)三角形面积的计算是直线与圆锥曲线的位置关系中的重点题型之一.在“设点”“设线”的解决思路,通过改“斜”归“正”,灵活运用“分割思想”为将三角形转化为底边与x轴平行的两个三角形面积之和;也可以通过弦长与高的计算,结合“韦达定理”进行代换消元,其缺点是运算较繁.此题变量较多,运算能力是解题成功的第一生产力,但变量多并不是盲目计算,而是寻找变量之间的联系,通过抽丝剥茧,化为单变量问题求解. “精致解题”还有什么思考要继续吗?我们发现试题中的“PA,PB的中点均在C上”这一几何条件并非关键性的,还可以从一般性将其推广,获得结论: 进一步将结论特殊化,当λ=0时,直线PA,PB的极限位置为点A,B处的切线,因而,我们又获得问题的数学史背景:试题中的△APB是抛物线的阿基米德三角形的一般情形,阿基米德三角形则是试题中△APB的极限状态.这样,以此题为窗口,我们将会看到阿基米德三角形的一些美妙性质,这是埋头做题所不能获得的数学体验.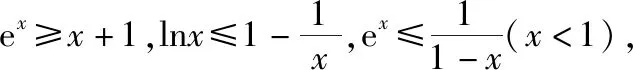
3.精致解题,加强基本技能训练