深度思考2018年全国卷Ⅰ文科第15题

广东

《普通高等学校招生全国统一考试大纲》(以下简称《考试大纲》)要求学生能够根据给定直线、圆的方程判断直线与圆的位置关系，能够用直线和圆的方程解决一些简单的问题，初步了解用代数方法处理几何问题的思想.虽然在近几年高考中“直线与圆的位置关系”的考题多为简单题或中档题，突出对基础知识与基本技能的考查，但既源于基础，又高于基础.考题不仅以选择题、填空题的形式出现，而且出现在解答题“坐标系与参数方程”之中，所以“直线与圆的位置关系”是一个大家需要高度重视的考点.

由于《考试大纲》是高考命题的依据，考题承担着落实《考试大纲》要求的任务，所以大家在备考“直线与圆的位置关系”的过程中，深度思考“2018年全国卷Ⅰ文科第15题”是十分必要的.本文重点阐述该如何对“2018年全国卷Ⅰ文科第15题”进行深入的研究，希望为师生备考2019年高考提供有益的借鉴.

一、考题及其解法

考题(2018·全国卷Ⅰ文·15)直线y=x+1与圆x2+y2+2y-3=0交于A,B两点，则|AB|=________.

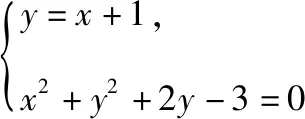
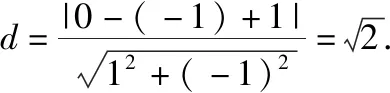
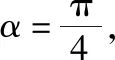
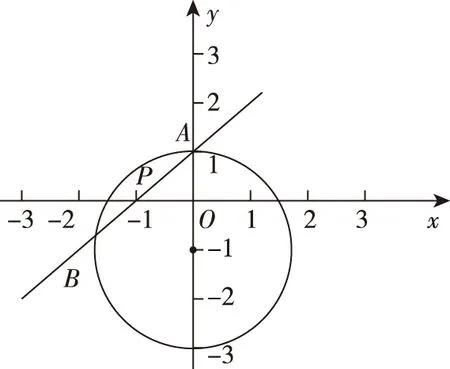
评注：本题考查的是直线与圆相交所成的弦长问题，难度不大，属于中档题.虽然解答此类问题有三种方法：“代数法”“几何法”和“参数法”，但是从上述的解答过程中不难发现：“几何法”是相对比较简单的方法.

二、如何确定直线与圆相交的位置关系

1.判断直线与圆相交的三种方法

变式1：已知直线y=x+1与圆x2+y2+2y-3=0，则直线与圆的位置关系为________.(相交，相切或相离)

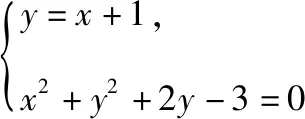
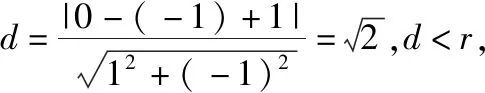
2.判断直线与圆锥曲线相交的通性通法

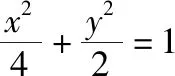
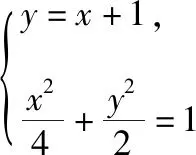
解法二(特殊法)：由于直线过定点P(-1,0)，并且定点P在椭圆内，所以过椭圆内定点的直线必与椭圆相交.

评注：判断直线与圆的位置关系通常有两种方法：“代数法”和“几何法”，当然也可以灵活运用类似上述的“特殊法”.虽然用“几何法”判断直线与圆的位置关系是相对较好的方法，也是教师优先向学生推荐的方法，但可惜的是，它不能推广到判断直线与圆锥曲线的位置关系，而“代数法”却可以.

三、如何求直线与圆锥曲线相交所成的弦长

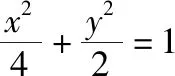
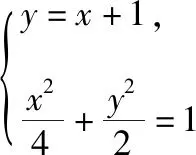
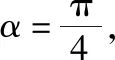
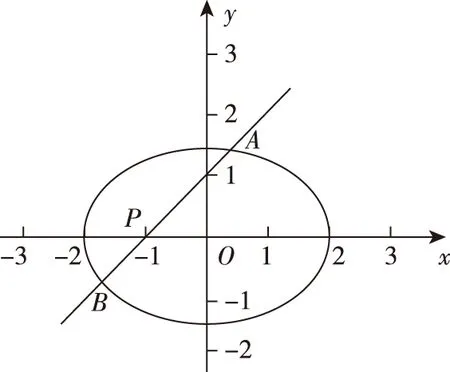
评注：求解“直线与圆相交所成的弦长问题”有三种方法：“代数法”“几何法”和“参数法”，并且教师优先向学生推荐的方法是“几何法”，但是求解“直线与圆锥曲线相交所成的弦长问题”的通性通法却是“代数法”和“参数法”.

四、还可以怎样对该题进行变式

1.过圆心的直线与圆相交

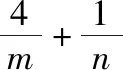
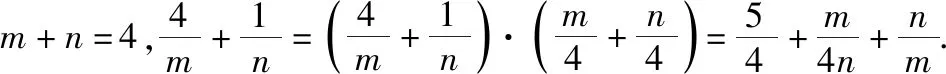
2.直线与圆相交的综合问题

变式5：已知直线l:y=x+m与圆C:x2+y2+2y-3=0交于A,B两点，且AC⊥BC，则实数m的值为________.

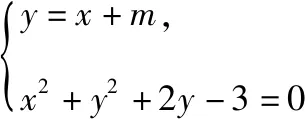
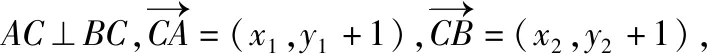
解法二(几何法)：由于AC⊥BC，所以△ACB为等腰直角三角形.

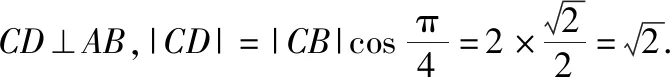
3.直线与圆相切

变式6：已知圆C:x2+y2+2y-3=0，过点A(m,0)的圆的切线仅有一条，则过点A的圆的切线方程为________.

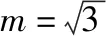
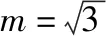
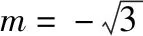
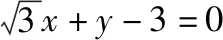
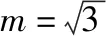
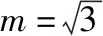
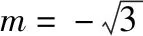
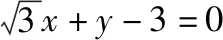
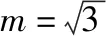
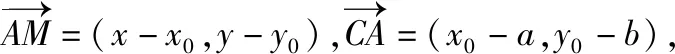
4.直线与圆相离

变式7：已知点A是圆C:x2+y2+2y-3=0上的动点，直线l:y=x-5，则点A到直线l的距离的最小值为________.

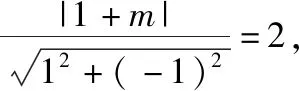
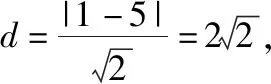
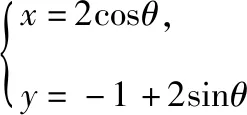
评注：“直线与圆相交”是高考的一个重要考点，常考的有：“判断直线与圆相交”“求弦长”和“与其他知识的综合问题”.大家从上述的解答过程中不难发现，用“几何法”解决上述问题是相对较好的方法.笔者认为：除了“直线与圆相交”之外，大家也必须理解“直线与圆相切”和“直线与圆相离”的相关知识，并熟悉掌握其解题方法.

五、怎样出现在“坐标系与参数方程”之中

变式8：(2018·全国卷Ⅰ文·22)在直角坐标系xOy中，曲线C1的方程为y=k|x|+2.以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ2+2ρcosθ-3=0.

(Ⅰ)求C2的直角坐标方程；

(Ⅱ)若C1与C2有且仅有三个公共点，求C1的方程.

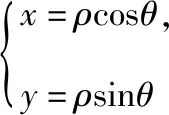
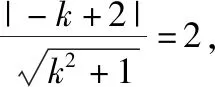
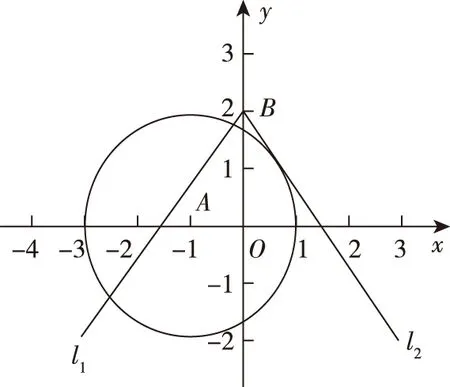
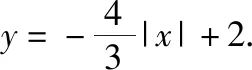
评注：在近几年的高考全国卷中，“直线与圆的位置关系”不仅以选择题或者填空题的形式出现，而且常出现在“坐标系与参数方程”之中，例如上述2018年全国卷Ⅰ文科第22题实际上就是“直线与圆的位置关系”的综合问题.