推陈出新 注重通法
——以2018年高考全国卷数学试题为例
广东
2016年10月,教育部考试中心姜钢主任在《中国教育报》上发表署名文章,正式提出了“一体四层四翼”的高考评价体系,其中“四翼”(即“怎么考”)是指“考查要求是从国家人才强国战略出发,结合高校人才选拔需求提出的基础性、综合性、应用性、创新性”,“创新性”主要体现在“学生要具有独立思考能力,具备批判性和创新性思维方式”.众所周知,现行高考命题实行的是“题库命题”,但肯定不会照搬原题.于是,如何推陈出新,体现试题的创新性,同时又要注重“通性通法”,成为了命题者需要考虑的一个大问题.
纵览2018年高考全国卷数学文理科6份试题,笔者发现,试题从“题目背景、题干要素、设问方式”等多角度进行了创新,体现“素养导向”的命题趋势,即考生通过分析、思考和比较,从题干中提取有用的信息,将已有知识和方法进行迁移,就能解决新的问题.可以说,这与考生考前刷题的数量是无关的.笔者汇总部分试题进行分析.
1.函数与导数
【例1】(2018·全国卷Ⅰ理·16)已知函数f(x)=2sinx+sin2x,则f(x)的最小值是________.
【分析】本题属于“题干要素创新”,以“三角函数的最值”为载体,考查考生运用导数工具,结合三角函数的周期性求解函数f(x)最值.但是大多数考生没有意识到这一点,认为解决三角函数最值的方法就是通过升幂、降幂转化为同角的三角函数,即y=Asin(ωx+φ)的形式,然后借助三角函数的图象解决问题.
【解答】第一步:求导得f′(x)=2cosx+2cos2x=2(2cosx-1)(cosx+1);
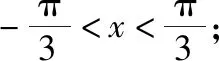
【例2】(2018·全国卷Ⅲ理·12)设a=log0.20.3,b=log20.3,则
( )
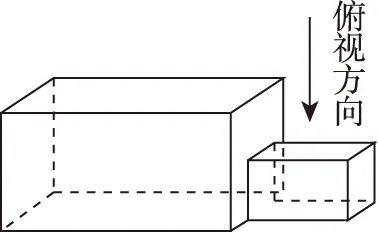
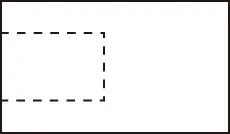
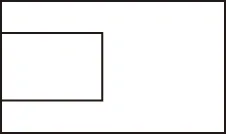
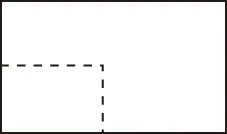
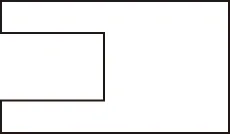
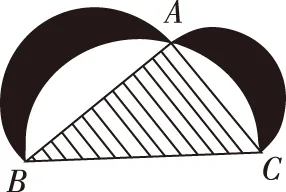
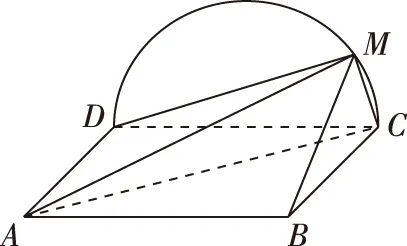
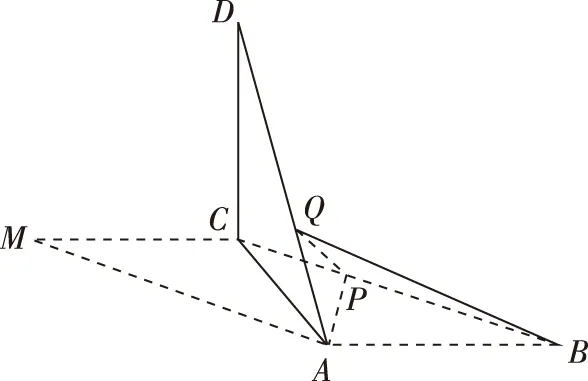
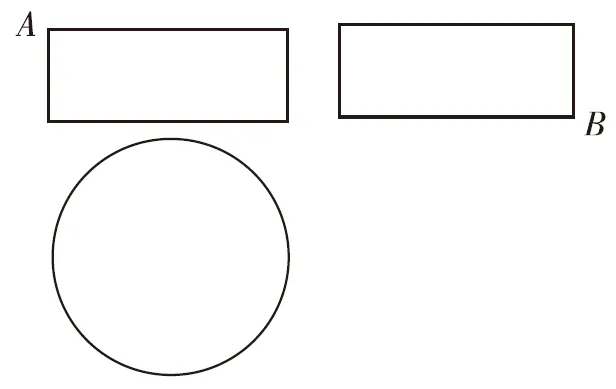
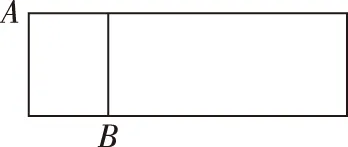
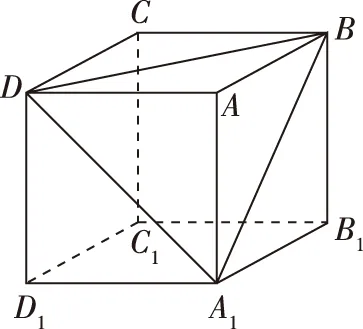
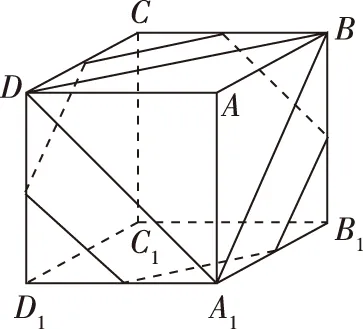
A.a+b C.a+b<0 【分析】本题属于“设问方式创新”,以“两个不同底数,相同真数的对数”为载体,比较它们的和与积的大小,并与0进行比较,考查考生通过构造基本初等函数运用作商法比较大小.但是,大多数考生没有进行深入分析,以为不同底数的对数难以比较大小,其和与积也不能运用对数公式进行合并,想不到逐层“剥茧抽丝”,只要转化成基本初等函数或运用作商法就能比较大小. 【解答】第一步:因为0 所以ab<0,且a+b<0,排除C,D; 而log0.30.4 ( ) 【分析】本题属于“题干要素创新”,以“直线与椭圆的位置关系”为载体,通常△PF1F2是椭圆的焦点三角形,但这里P点在过左顶点的一条直线上,本题考查考生运用数形结合等思想方法,“用代数方法解决几何问题”的能力. 【分析】本题属于“题干要素”与“设问方式”双创新,通常是要求椭圆的方程,但本题先给出一个特殊的椭圆与一个中点,要求参数的范围;而第(Ⅱ)问中则由平面向量给出关系式,证明三条线段的长度成等差数列,涉及知识点较多,综合性较强.由下面解答过程可知,本题其实还是强调通性通法,(Ⅰ)中的解法二其实是解决中点问题的常规方法——点差法,而(Ⅱ)中由于没有学习椭圆的第二定义,但是由两点距离公式可以轻松解决焦半径的问题. 【例5】(2018·全国卷Ⅰ·理7,文9)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为 ( ) C.3 D.2 【分析】本题属于“题干要素”与“设问方式”双创新,以“三视图”为载体,常规的考法是把三视图还原成直观图,再求其面积或体积,而这里是考虑到直观图的展开图,将曲面问题转化为平面问题,运用“两点间线段最短”求解,计算并不困难,重点考查了考生“直观想象”的素养. 【解答】第一步:沿过点A的母线把圆柱侧面展开,A,B(B为下底边四等分点)的位置如图所示; 【例6】(2018·全国卷Ⅰ理·12)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为 ( ) 【分析】本题是一道改编题,在“设问方式”上有所创新,原题要求正方体十二条棱与某一截面所成角相等时线面角的值,而本题的创新之处在于“求满足条件的截面中,面积最大的一个”.显然,本题的设问对学生的“直观想象”的数学素养要求更高,若考生在第二步中运用构造函数的方法求解最值,则丧失了本题的意义,也把简单问题复杂化了. 【解答】第一步:找出符合条件的其中一个截面. 第二步:找出与截面A1BD平行的截面中面积最大的一个. 【例7】(2018·全国卷Ⅱ理·8)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是 ( ) 【分析】本题属于“背景创新”,选取了“哥德巴赫猜想”这一至今未解决的世界数学猜想问题,我国数学家陈景润在这方面取得了世界领先的成果这一背景.利用这一深刻的数学背景,引导正确的价值观. 【例8】(2018·全国卷Ⅲ理·8)某群体中的每位成员使用移动支付的概率都为p,各成员的支付方式相互独立.设X为该群体的10位成员中使用移动支付的人数,DX=2.4,P(X=4) ( ) A.0.7 B.0.6 C.0.4 D.0.3 【分析】本题属于“背景创新”,选取了“互联网+”时代一个便捷的生活方式——移动支付,也是被称为中国的“新四大发明”之一这一背景,体现了高考数学试题与时俱进,数学来源于生活的本质. 【解答】第一步:据题意,本题考查的是独立重复试验,对应的是二项分布,所以DX=10×p×(1-p)=2.4,则p=0.4或p=0.6,排除A,D; 【例9】(2018·全国卷Ⅲ·理3,文3)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是 ( ) A B C D 【分析】本题通过“中国古建筑借助榫卯将木构件连接起来”这一文化背景,考查三视图的知识,渗透了数学文化,旨在继承和弘扬中国传统文化. 答案:A. 【例10】(2018·全国卷Ⅰ理·10)下图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC,△ABC的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ.在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p1,p2,p3,则 ( ) A.p1=p2B.p1=p3 C.p2=p3D.p1=p2+p3 【分析】本题以古希腊数学家希波克拉底发现的一个优美的定理——“蝴蝶定理”为背景,借助几何概型,让考生从中体会到了数学的美. 答案:A. (Ⅰ)证明:平面AMD⊥平面BMC; (Ⅱ)当三棱锥M-ABC体积最大时,求面MAB与面MCD所成二面角的正弦值. 答案:(Ⅰ)证明略. 【例12】(2018·全国卷Ⅰ文·18)如图,在平行四边形ABCM中,AB=AC=3,∠ACM=90°,以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA. (Ⅰ)证明:平面ACD⊥平面ABC; 【分析】本题的创新之处在于给出的图形并不是一个组合体,而是由简单的线、面组成的一个图形,图形简洁明了,运用“通性通法”即可轻易解决. 答案:(Ⅰ)证明略. (Ⅱ)三棱锥Q-ABP的体积为1. 从以上分析可以看出: (1)高考中“创新题型”成为一种趋势,起初给考生的感觉是似曾相识,但又不易觉察,若考生认真分析过后,却发现恰是“邻家女孩”; (2)全国卷Ⅰ、Ⅱ、Ⅲ中,卷Ⅰ、Ⅲ的“创新题型”较多,卷Ⅱ偏少; (3)文理分类中,理科卷比文科卷的“创新题型”要多; (4)在各知识模块中,函数与导数、立体几何、统计概率出现“创新题型”的几率较大. 任子朝先生曾指出“高考试题”的命题方向:从能力立意到素养导向的转变,突出表现为考查目的从关注知识到关注人;考核目标从常规性的问题解决技能到创造性的探究能力;考查情境从学科知识到真实情境;试题条件从结构良好到结构不良;试题要素从单一因素到复合因素;试题结构从碎片到整体. 笔者认为,通过高考试题的分析,对今后的教学和备考有以下几点启示: (1)夯实基础知识,提炼思想方法 数学知识是数学素养的外在表现,只有通过思想方法的提炼才能够实现素养的发展.在教学中,教师要注意加强基本概念、基本定理的教学,总结数学概念和定理中隐含的思想方法,把握数学问题的本质,这样学生就能做到融会贯通、举一反三.弗莱登塔尔说过:“真正能够起到思维训练作用的是数学思想方法而不是具体的题材,因而必须强调方法,并尽可能使其明确.”在教学中,教师可以设计具有探索性和研究性的问题,让学生在分析和思考的过程中培养数学思维,提炼数学思想.在数学思维教学中,教师可以不失时机地进行提问,引导和启发学生展开思考和讨论,领悟其中的思想方法. (2)重视解题教学,突出通性通法 在数学学习的过程中,学生需要花费相当多的时间进行解题,“如何开展解题教学”是教师必须面对的问题.卢梭说:“教大多数学生能想到的方法,教育效法自然.”在教学中,教师要教学生学会思考,学会研究问题的一般方法,即通性通法,要注重对通性通法的归纳和总结,对问题不仅要知其然,更要知其所以然.通过解题和反思活动,充分挖掘典型试题的内在价值和迁移功能,通过一题多解,一题多变和创新题来培养学生的思维能力和创新意识. (3)积累活动经验,发展核心素养 新课标要求,学生通过高中数学的学习,进一步获得学习以及未来发展必需的数学基础知识、基本技能、基本思想和基本活动经验.教学中,教师要注重学生数学活动经验的积累:一是重视数学对象的获得过程,从现实或数学事实出发,让学生经历归纳、概括事物本质的过程,学会用数学的眼光观察世界;二是重视让学生经历数学对象的研究过程,以“一般观念”为引导发现规律、获得猜想、证明结论,学会用数学的思维思考世界;三是在应用数学知识解决问题的过程中,重视利用数学概念原理分析问题、解决问题的过程,学会分析数据,从数据中挖掘信息等,学会用数学的语言表达世界.教师可以通过设计有意义、适度的问题,引导学生经历上述过程并概括出数学的本质,逐步积累学生数学活动的经验,发展学生的数学核心素养. (4)注重知识整体,构建知识网络 新课标强调开展主题教学,分阶段、分步骤加以实施,目的是构建知识的整体和联系,逐步提升学生的数学核心素养水平.在教学中,我们要深入理解、整体把握教学内容,从数学学科的整体结构、核心内容和重要思想上整体把握和认识数学教学内容,完整地体现好数学的科学性、工具性、价值理性和人文性这些特质.我们要理清各知识之间的联系,构建知识网络,做到知识和方法的融会贯通,这样才能以逸待劳,以不变应万变,决胜高考考场.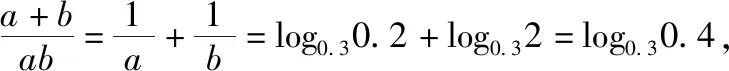
2.解析几何
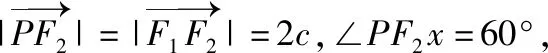
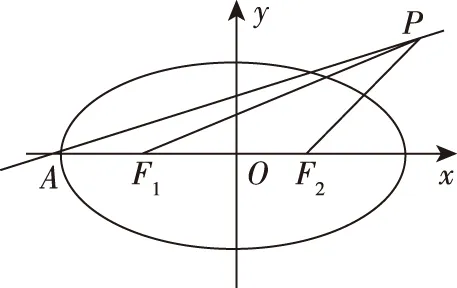
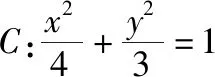
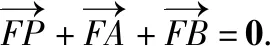
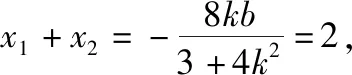
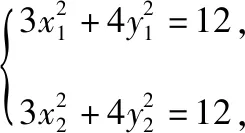
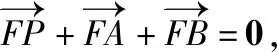
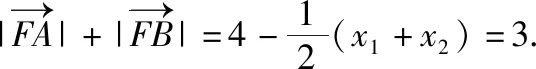
3.立体几何
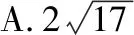
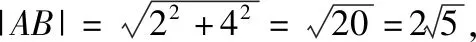
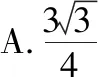
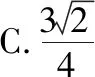
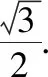
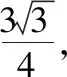
4.统计概率
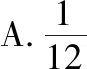
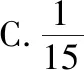
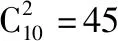
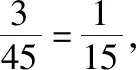
5.其他题目