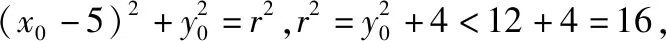活用二级结论，巧解选填试题

湖南

通过基本性质、定理、公式推导出来并广泛应用的结论性质被称为“二级结论”.二级结论把程序性知识固化为结果性知识，形成知识组块.二级结论的核心在于帮助学生在考试中迅速的利用一些“快准狠”的结论来解答一些问题，以实现分数快速提高.在高考数学复习中笔者发现，及时归纳并总结一些常用的二级结论，对于学生提高解题成功率、缩短运算时间非常有帮助.下面将高考试题中经常出现而且教材上有所体现的部分二级结论呈现给大家,部分结论对学生的解题有很好的指导作用,同时对演算结果有精准的验证作用,以便同学们在解答高考题时做到准确、快捷.

一、函数问题中常用二级结论

结论一 奇函数的最值性质

已知函数f(x)是定义在集合D上的奇函数,则对任意的x∈D,都有f(x)+f(-x)=0.特别地,若奇函数f(x)在D上有最值,则f(x)max+f(x)min=0,且若0∈D,则f(0)=0.

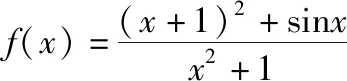
【答案】2

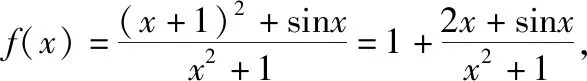
【点评】奇函数的图象关于原点对称，那么它的最大值和最小值点肯定也关于原点对称，也就是最大值和最小值互为相反数.本题型的解题方向就是设法将函数解析式进行分解，尽量分离出一个奇函数和常数或者具有单调性的部分，以达到速解目的.

结论二 抽象函数的对称性

已知函数f(x)是定义在R上的函数.

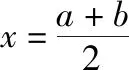
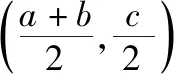
【例2】已知函数y=f(2x+1)是定义在R上的奇函数，函数y=g(x)的图象与函数y=f(x)的图象关于直线y=x对称，则g(x)+g(-x)的值为

( )

A.2 B.1

C.0 D.不能确定

【答案】A

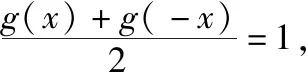
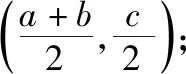
结论三 周期函数问题

已知定义在R上的函数f(x),若对任意的x∈R,总存在非零常数T,使得f(x+T)=f(x),则称f(x)是周期函数,T为其一个周期.

常见的与周期函数有关的结论如下:

1.如果f(x+a)=-f(x)(a≠0),那么f(x)是周期函数,其中的一个周期T=2a.

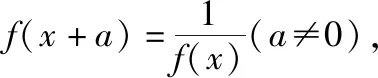
3.如果f(x+a)+f(x)=c(a≠0),那么f(x)是周期函数,其中的一个周期T=2a.

4.如果f(x)=f(x+a)+f(x-a)(a≠0),那么f(x)是周期函数,其中的一个周期T=6a.

5.若函数f(x)具有对称轴x=a，x=b(a≠b)，则f(x)为周期函数且一个正周期为|2a-2b|.

6.若函数f(x)具有对称中心(a,0)，(b,0)(a≠b)，则f(x)为周期函数且一个正周期为|2a-2b|.

7.若函数f(x)具有对称轴x=a和对称中心(b,0)(a≠b)，则f(x)为周期函数且一个正周期为|4a-4b|.

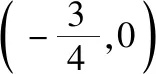
【答案】A

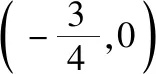
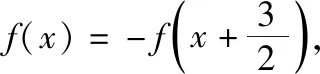
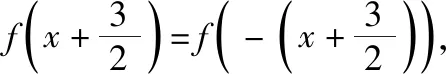
所以f(x)为偶函数.

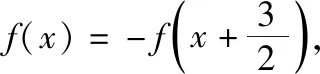
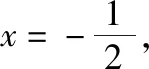
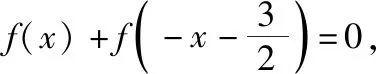
于是f(1)+f(2)+f(3)=1+1-2=0，

所以f(1)+f(2)+…+f(2 019)=673×(f(1)+f(2)+f(3))=0.

【点评】函数的对称性与周期性结论因为相似度高，运用时容易混淆.区分的关键是括号内x的系数符号“同号看周期，异号看对称”.本题给出了对称性和周期性的条件，需要分别利用对称性和周期性结论，发现f(x)的奇偶性和周期性，进而得到问题的解答.

二、空间立体几何中常用二级结论

结论四 多面体的外接球和内切球

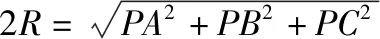
2.已知三棱锥P-ABC，PA⊥平面ABC，若PA=a，△ABC的外接圆半径为r，则该三棱锥P-ABC的外接球半径R满足(2R)2=(2r)2+a2.

3.棱锥的两个侧面互相垂直，已知两个相互垂直的面的外接圆半径的长及其公共棱的长度的情形：已知三棱锥A-BCD中，面ABD⊥面BCD，且△ABD，△BCD的外接圆半径分别记为r1,r2，公共棱BD=a，则该三棱锥的外接球半径R满足：(2R)2=(2r1)2+(2r2)2-a2.

【例4】在《九章算术》中，将四个面都为直角三角形的三棱锥称之为鳖臑.已知在鳖臑M-ABC中，MA⊥平面ABC，MA=AB=BC=2，则该鳖臑的外接球与内切球的表面积之和为________.

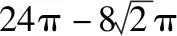
【解析】设MC的中点为O，如图，

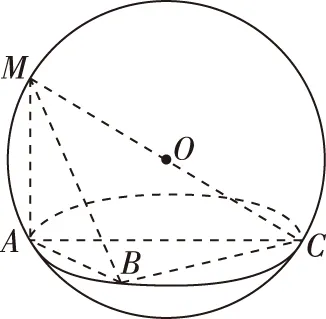
由AB=BC=2，且△ABC为直角三角形，得∠ABC=90°.

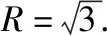
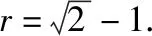
【点评】求多面体的外接球和内切球的策略不同，外接球尽量通过补形法或直接利用已有结论计算半径(或者直径)，而内切球常常利用等体积法来求.本题由条件不难看出球的直径就是三棱锥的侧棱MC，也可直接将三棱锥补形成正方体.而内切球的半径由割补法，把三棱锥切割成以各面为底，球心为顶点的四个三棱锥，再利用三棱锥体积相等求半径.

三、解析几何中常用二级结论

结论五 焦点三角形的面积公式

( )

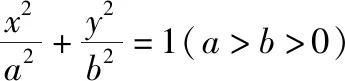
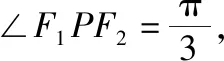
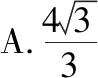
C.3 D.2

【答案】A

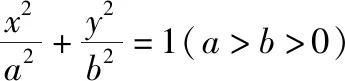
【点评】本题的巧妙之处在于利用椭圆与双曲线的焦点三角形面积公式，得到椭圆的半短轴与双曲线的半虚轴之间关系，再利用焦距相等，转化成两种曲线的离心率之间的关系，通过三角函数换元，进而求出椭圆和双曲线的离心率的倒数之和的最大值.

结论六 圆锥曲线的切线问题

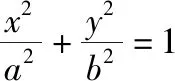
2.已知点M(x0,y0),抛物线C:y2=2px(p≠0)和直线l:y0y=p(x+x0).

(1)当点M在抛物线C上时,直线l与抛物线C相切,其中M为切点,l为切线.

(2)当点M在抛物线C外时,直线l与抛物线C相交,其中两交点与点M的连线分别是抛物线的切线,即直线l为切点弦所在的直线.

(3)当点M在抛物线C内时,直线l与抛物线C相离.

【例6】已知抛物线C:x2=4y,若点P为抛物线C的准线上的任意一点，过点P作抛物线C的两条切线PA,PB,其中A,B为切点,直线AB恒过定点为________.

【答案】(0,1)

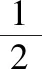
【点评】探究直线恒过定点问题，常常利用题设条件写出目标直线的含参方程，由参数的任意性可得定点.利用圆、椭圆、抛物线已有切线结论，往往可以化繁为简，达到速解目的.

结论七 圆锥曲线的中点弦问题

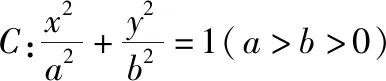
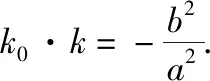
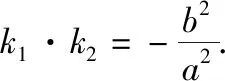
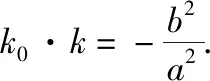
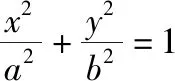
【例7】设直线l与抛物线C:y2=4x相交于A,B两点，与圆(x-5)2+y2=r2(r>0)相切于点M，且M为线段AB的中点.若这样的直线l恰有4条，则r的取值范围是________.

【答案】2

【解析】当直线l的斜率不存在时，必有两条垂直于x轴的直线和圆相切且满足线段AB的中点为切点；

当直线l的斜率存在时，设斜率为k，A(x1,y1),B(x2,y2),x1≠x2,M(x0,y0),由上述结论得ky0=2.