基于理解，细化过程，渗透思想

陶继智

[摘  要] 平面向量是高中数学的重难点知识，由于向量的矢量性，学生在理解时存在一定的难度，对于该部分内容的教学需要从易于理解的角度出发，结合学生的知识经验来开展. 而对于平面向量的概念、定理教学，应采用探究式的教学方式，并且充分渗透数形结合思想，从“数”与“形”的角度揭示向量特性，促进学生知识、能力和思想的综合提升. 文章将从情境理解、过程探究、思想渗透三个方面开展“平面向量”知识的教学讨论，与同行交流学习.

[关键词] 平面向量;理解;过程;思想;数形结合

向量是高中数学的重要概念，它是代数与几何的共同研究对象，是沟通两者联系的桥梁. 从教学视角来看，平面向量知识的教学不同于以往内容，由于其自身的丰富背景和学科联系使得实际教学存在一定的难度，若不能准确把握教材内容，合理编排教学环节，则会造成学生理解障碍，影响课堂教学效果. 以下是笔者对于“平面向量”相关知识的教学建议.

[?]基于学生理解，开展情境教学

平面向量是一种较为特殊的量，对于学生而言还很陌生，因此起始教学时需要基于学生理解，从学生已有的知识经验和生活经验的基础上来开展，通过对已有经验的发展和完善来构建新知，并将其纳入学生的知识体系中，提升学生灵活应用知识的能力.

对于平面向量的理解性学习策略，可以引入问题情境，通过对问题的讲解帮助学生理解平面向量. 教学中直接引出向量会造成学生理解困难，可以先从路程和位移的认识开展教学，比如设置如下情境：有一蜘蛛织了一张边长为15 cm的正六边形的网，它位于网的中心O，蚊子在点A处，如图1. 让学生思考蜘蛛走怎样的路线可以吃到蚊子，蜘蛛是不是只要爬行15 cm就一定可以吃到蚊子. 以六边形为基础，从不同路径入手，让学生初步理解路程与位移之间的区别，为后续的向量引出做基础.

由于在中学物理中学生已经学习了力与速度的分解问题，可以以此为教学的情境素材，结合已学知识，利用实际问题来开展进一步的概念教学，通过力的分解引出向量，教学中可以设置如下问题：在一斜面上有一重物，自身所受重力为G，可将其分解为物体沿斜面的下滑力F1和垂直于斜面的压力F2，如右图2所示. 物理上用G=F1+F2来表示三者之间的关系，引导学生理解上述三个量不仅具有大小性，还具有方向性，通过这样的类比学习可以直指向量概念.

以生活原型为教学素材，联系物理学相关知识来引申平面向量，这样的教学方式是从学生理解的角度来开展，是旧知向新知完美过渡的过程，对于学生理解向量概念极为有利. 另外从实际问题中引申向量也是对向量应用性的充分体现，有利于后续向量应用性教学.

[?]注重形成过程，细化设计环节

对于向量的起始教学，让学生充分体验向量概念、定理的形成过程是十分必要的，无论是概念、定理的猜想阶段，还是对其科学性的论证阶段，都需要精心设计教学环节，让学生充分思考，积极讨论，通过自身的实践探究来理解概念的内涵.

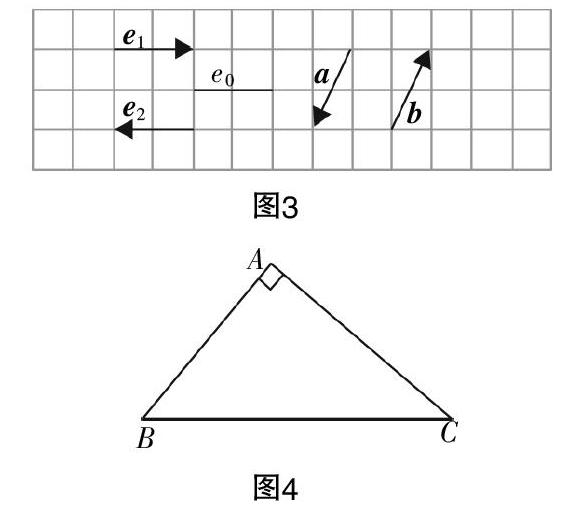
学生对于向量的几何表示是从物理问题的矢量性画法中引出的，而对于向量的符号表示，即利用有向线段表示向量，则需要教师通过设问的方式来不断引导，让学生理解向量的方向性是其本质属性. 教学中可以在方格纸上绘制向量和直线，如图3所示，首先让学生思考e0和e1的异同，学生很容易就会发现e1具有箭頭，而e0没有;然后让学生思考e1和e2之间、a和b之间的区别，从而使学生认识向量的方向性，并理解方向是向量的本质属性. 在此基础上引出几何中向量的表示方法，结合直角三角形，如图4所示，让学生理解和所表示的含义是不同的，初步掌握数学上向量的表示方法. 设计这样的教学过程使向量概念从实际问题上升到了数学的符号高度，充分体现数学符号表示向量的重要特征.

而在向量概念的学习阶段，还需要引导学生学习向量关系，可以设计如下环节：在图5所示的正六边形ABCDEF中画出一些向量，并用数学符号将其表示出来，学生以小组为单位比较一下所画向量之间存在何种关系，并总结向量之间具有哪些关系. 由于正六边形具有一定的特殊性，图形上的短线段均等长，从而直接将向量比较限制在其方向性上，通过这样的对比、讨论、总结的方式，学生可以较为直观地获得向量的“相等”“相反”“共线”和“平行”关系.

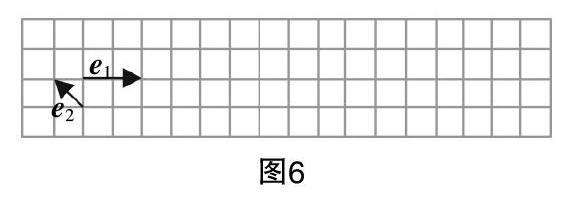
对于平面向量基本定理的学习，同样可以设置探究的学习环节，让学生通过画图、分析、讨论的方式来掌握定理，可以借助几何画板，指导学生在图6中结合非零向量e1和e2，作出向量a=3e1+2e2以及向量b=-e1+2e2，然后让学生思考如果给出任意实数λ1和λ2，是否可以作出形如λ1e1+λ2e2的向量，进一步设问让学生思考向量a是否可以表示为λ1e1+λ2e2的形式以及需要满足哪些条件. 通过画图实践、设问引导、独立思考的教学活动，学生可以逐步归纳基本定理，为后续的定理深入理解做基础.

新课改下的教学课堂应该是学生参与、教师引导的实践课堂，学生对知识的探索过程远远比结果重要，因此无论是在向量概念，还是定理学习中都应该设计多样的实践活动，关注学生的思维过程，适时引导，让学生在掌握知识的前提下获得探究实践技能，逐步形成科学、严谨、逻辑的数学思维，这才是过程教学的重要意义.

[?]渗透思想方法，数形结合教学

向量建立了代数与几何之间的联系，不仅具有代数精准和几何直观的双重特性，还在思想方法上对两者完成了继承，教材的编写也在无形中对两者的数学思想进行了渗透. 因此对于向量内容的教学也不能仅限于知识本身，而抛弃知识背后的思想精华.

向量的运算容易使学生产生向量纯属代数知识的错误认识，但由于向量的方向性，以及运算规律是基于几何图形的，因此向量知识同样需要从几何角度来分析. 因此在向量教学中需要采用数形结合的方式，充分渗透数形结合的教学思想，引导学生从几何代数化、代数几何化等多角度进行思考. 尤其在对一些定理进行证明时，需要引导学生从“数”与“形”的角度来分析，如证明定理“a⊥b?

向量知识有很强的实用性，在向量有关问题计算时同样可以渗透数形结合思想，可给出关于向量积问题：如图8所示，点E为直线BC上的一点，现已知=2，求·的值. 在向学生讲解时可以采用建立直角坐标系的方式，利用坐标系兼具“数”与“形”的特点，向学生传达数形思想. 首先让学生以点A为坐标原点，AB为x轴，AC为y轴建立直角坐标系，令点B（3，0），C（0，b），引导学生根据条件求得点E的坐标，并计算和，然后利用向量积的知识求值. 这样的解题方式充分渗透了数形结合思想，图形分析关系，代数辅助计算，实现了“数”与“形”的完美结合.

向量知识背后的数形结合思想是对向量的几何、代数本质属性的体现，在向量的定理教学、解题教学中充分渗透该思想，不仅可以使学生对向量知识产生深刻的理解，而且可以使学生掌握数学的思想方法，促进学生思想的提升，而后者思想的提升对于学生的长远发展更为有利.

[?]结束语

平面向量具有几何和代数的双重特性，对于该部分内容的教学具有一定的挑战性，不同于代数与几何的单一视角，向量的教学需要充分转化视角，实现两者的完美结合. 在实际教学中，可以依照课标要求，以理解性学习作为教学基准，在学生已有知识经验的基础上构建向量的知识体系;注重知识的形成过程，开展实践探究，让学生充分参与课堂教学，获得知识和技能的双重提升;而在具体教学中要注意思想方法的合理渗透，对于向量定理以及解题应用，采用数形结合的教学方式，发展学生的数学思维，促进学生智力与能力综合发展.