积分中的函数归零问题探究

高婷婷，张明会

函数归零问题，是数学分析中，也是历年各类考试中，经常出现的一类重要问题［1-2］.因此，对这类问题进行研究一直是数学分析问题研究中的热点问题.函数归零问题就是在满足一定已知条件下，进行一系列的逻辑推理，进而达到证明函数在某一区间上恒为零的问题.即在一定条件下证明f(x)≡0 的问题［3-4］.2004年，邓乐斌给出了函数归零问题的几种证法［5］.2009年，苏化明给出了函数归零问题的常用解法［6］.2011年，李腾给出了关于函数零点存在性的几种判别方法，但这些论文中的归零问题，都是在非积分情况下进行的.因此，本文在以往研究问题的基础上，给出了函数在积分情况下的归零问题，即在区间，可以得到f(x)≡0的一些积分条件.

1 基础知识

引理1［7］设f(x)是区间[a,b]上连续的非负函数，则时必有f(x)≡0，x∈[a,b].

引理2［7］设函数f(x)在区间[a,b]上连续，则时必有f(x)≡0，x∈[a,b].

引理3［7］设函数f(x)在区间[a,b]上连续，若对 [a,b]上的任何连续函数φ(x)，均有，则在[a,b]上f(x)≡0.

说明：在引理2成立的情况下，当取φ(x)=f(x)时，即可证得本定理结论成立.

引理4［7］已知函数f(x)在 [a,b]上连续，则对 ∀ε＞0 ，存 在 多 项 式p(x)，使 得，对∀ε∈[a,b]成立.

2 主要结果

定理1设函数f(x)在对称区间[-a,a](a＞0)上连续，若对[-a,a](a＞0)上每一个(R)可积的奇函数或偶函数φ(x)，均有，则在[-a,a]上f(x)≡0.

证明 先证函数f(x)必为[-a,a]上的偶函数.

用反证法：设函数f(x)在[-a,a]上不是偶函数，则 ∃x0∈[-a,a]，使f(x0)≠f(-x0)，为了方便，我们设x0∈(-a,a)，且f(x0)＞f(-x0).

（1）若f(-x0)≥0，则f(x0)＞0，由于f(x)在点-x0和x0连续，∃δ＞0，使得

当x∈[-x0-δ,-x0+δ] 时 ，有f(x)＞成立；

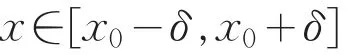
当 时，有成立.

再作[-a,a]上的偶函数φ(x)如下：

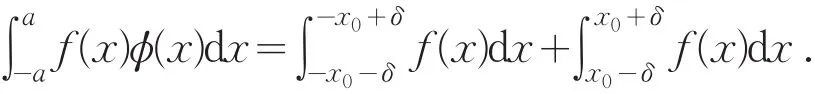
又由积分第一中值定理，可以得到

于是

而这与已知条件矛盾.

（2）若f(x0)≤0，考虑 -f(x)，同（1）证明仍可得

（3）若f(-x0)＜0＜f(x0)，∃δ＞0，使x∈[-x0-δ,-x0+δ]时，f(x)＜0 ；x∈[x0-δ,x0+δ]时，f(x)＞0.

此时再作[-a,a]上的奇函数

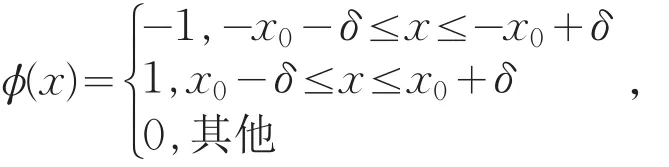
仍由积分第一中值定理，得到

此结论与已知条件矛盾，由此知道函数f(x)是[-a,a]上的偶函数.

同理可证，f(x)也是[-a,a]上的奇函数.

由于f(x)在[-a,a]上既是奇函数又是偶函数，因此f(x)≡0,x[-a,a].

定理2设函数f(x)在区间[a,b]上连续，且对k=1,2,…,n-1，有，证明f(x)≡0或在(a,b)内至少改变n次符号.

为了解独立学院非英语专业学生听力能力的现状，本文以中原工学院信息商务学院2017级非英语专业的3848名本科学生为研究对象。其中，招生总人数为4166，其中318人因各种原因未参加测试和调查。受试学生分别来自我校的8大系37个专业。其中，艺术类专业学生887人，普通文科专业学生1664人，普通理科专业学生1297人。

证明 由题干条件，对任何r次多项式

p(x)(0≤r≤n-1)，有

反设f(x)不恒等于零，而在(a,b)内f至多改变n-1次符号，为确定计数，设改变了r+1次符号.这里r+1≤n+1，则存在r个点x1,x2,…,xr，使在以下每个小区间

内f(x)不变号，并且在相邻两个小区间内f(x)异号.

考虑r次多项式p(x)=(x-x1)(x-x2)…(x-xr)，p(x)也在上述每个小区间内不变号，且在相邻两个小区间上异号，于是函数f(x)p(x)在[a,b]上连 续 且不 变号 ，由，即 得f(x)p(x)≡0.注意到p(x)仅在有限个点处为零和f(x)在[a,b]连续，即得f(x)≡0，x∈[a,b].矛盾.

定理3设函数f在[a,b]上连续，且对任何n=1,2,…, 有.证 明f(x)≡0 ，x∈[a,b].

其中，∀ε∈[a,b].注意到，有

定理4设函数f(x)在[a,b]上连续，且在

[a,b]上成立，证明：f(x)≡0，x∈[a,b].

证明 已有f(x)≥0，现证f(x)≤0.

令G(x)=g(x)e-x，G′(x)=g′(x)e-x-g(x)e-x=e-x(g′(x)-g(x))≤0.G′(x)为单调递减函数，又G(a)=0，因此在[a,b]上G(x)≤0，即g(x)e-x≤0，而e-x＞0，得g(x)≤0，于是g′(x)≤0，f(x)=g′(x)＜0，即f(x)≤0.这样就有f(x)≥0且f(x)≤0 ，即f(x)≡0，x∈[a,b].

定理5设函数f(x)在(-∞,+∞)内连续，证明：若函数内递减，则在(-∞,+∞)内f(x)≡0.

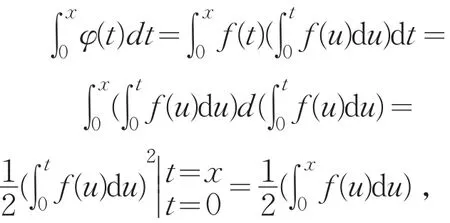
定理6 函数f(x)在 [α,β]上连续，若对[α,β] 上 的 任 意 连 续 函 数w(x) 成 立g(α)=g(β)=0 ，且 ∫α βf(x)w(x)dx=0 ，则在 [α,β]上，f(x)≡0.

证明 若函数f(x)在x0处不为零，不妨令f(x0)＞0，从而由函数连续性定理知道，一定存在U(x0)⊂[x1,x2]⊂[α,β]，使得0.此时可取函数

于是可知w(x)一定满足定理条件，则

易知此式矛盾，则在[α,β]上，f(x)≡0.

3 结论

函数归零问题，在数学分析教材中、硕士研究生入学考试中都是频繁出现的重要问题.本文在以往研究结果的基础上，将函数归零问题推广到了积分中的情形，即在区间[a,b]上得到f(x)≡0的一些积分条件，得到了几个重要的结论，为不同情形积分下的证明和应用提供了理论依据.与此类似，今后还可考虑将函数归零问题再推广到其他数学知识点中，这方面有待于进一步深入研究.