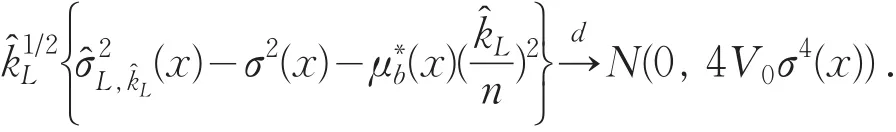波动率函数的局部线性K-nn估计

叶绪国，龙伟芳

考虑连续扩散过程{Xt, 0≤t≤T}的波动率函数σ2(⋅)估计问题，且其过程描述为微分方程

dXt=μ(Xt)dt+σ(Xt)dWt， （1）

其中，μ(⋅)和σ(⋅)分别叫做漂移项与波动率项，Wt是一个标准布朗运动.

目前波动率函数的非参数估计研究现已有很多结果［1］.特别地，Fan和Yao［2］提出局部线性估计技术估计波动率.然而，当在其支撑内数据分布不均，那么带有固定窗宽的局部线性滑动估计量可能在某个支持区域内存在极少数据，从而导致不稳定统计推断.一些数据驱动技术用于解决自动窗宽选择问题［3］，但涉及繁重的计算，且需要额外的努力实现执行.作为核估计的一个备选方法，在估计密度函数或回归函数时，部分学者建议使用带有随机窗宽且拥有收敛速度相同的K-nn估计.欧阳德生等人［4］使用其估计回归函数.然而，局部线性K-nn估计技术并未使用于波动率函数估计.因此，本文将探讨该方法应用于波动率函数估计，同时建立估计量的渐近性质，并证明了带有交叉验证（CV）技术选取参数k的K-nn估计渐近行为类似于带有交叉验证（CV）技术选取参数k的核估计的表现.

1 波动率函数的局部线性K-nn估计

设Δt为取样间距，设由模型（1）生成而得历史数据为那么，基于Fan和Zhang，对于模型模型（1）使用Euler近似，可得

其中，εi～i.i.dN(0, 1)，i=1, 2,…,n.现在考虑波动率函数的局部线性K-nn估计.固定x，定义kn近岭距离，即所有Xti到x中第kn最近欧氏距离其中表示欧氏距离，且Rn，i=1, 2,…,n}.或者也定义到Xti的kn近岭距离为所有Xtj(j≠i)到Xti中第kn最近欧氏距离.

如果在公式（2）中函数m(⋅)是已知的，于是，基于E(S2|Xt=x)=σ2(x)，我们视估计σ2(x)问题为非参数估计问题，其中S2=(Y-m(Xt))2.给定来自模型（1）的观察样本点{(Xti,Yi), 1≤i≤n}，我们写S2i=(Yi-m(Xti))2.

定义δ(x)=(σ2(x),σ˙2(x))T，其中σ˙2(x)表示σ2(x)的一阶导函数.对于x∈R，δ(x)的局部线性K-nn估计量为

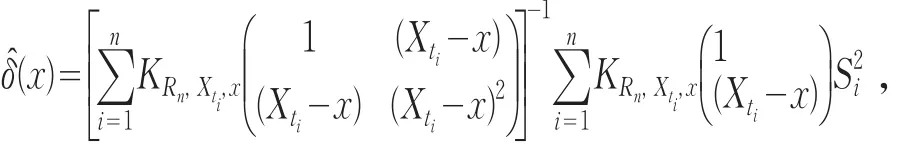
当函数m(⋅)一般是未知的，为了得到m(x)和σ2(x)的非参数估计，利用由欧阳德生等人［4］提出的局部线性K-nn估计技术.令mˆ(x)=αˆ1表示m(x)的局部线性K-nn估计量，且具体形式可由解加权最小二乘问题而得，即

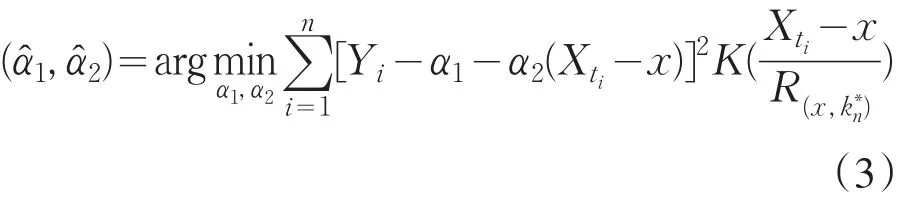
从而，δ(Xti)的去一局部线性估计量表示为

定义一个首位元素为1，其他为0的2×1向量e1，定义的去一局部线性估计量.为了更好的估计波动率，应讨论如何选择参数k，于是，这里提出最小二乘CV方法，即选择使得函数CVL(k)最小化

其中，M(⋅)是支持紧集函数，以便避免中分母过小.于是是基于公式（6）的参数k下的σ2(x)局部线性K-nn估计量.

2 估计量的渐近性质

首先，介绍下列一些假设.

A1.存在常数C，使得E|μ(Xs)|2(p+δ)≤C，E|σ(Xs)|2(p+δ)≤C，∀s∈[t-η,t]，其中η是正数，p是不小于2的正数，且δ＞0.

A2.函数m(x)、p(x)和σ2(x)是四阶连续可微.给 定x，p(x)＞0 ，σ2(x)＞0 和 函 数E(Y4|X=x)是在x处连续，其中p(x)是Xt的概率密度函数.

A3.M是函数M(⋅)的支撑，那么存在δ，有

A4.核函数K(⋅)是一个有界对称非负密度函数. 进 一 步 ，∫K(x)dx= ∫‖x‖＜1K(x)dx=1 ，当‖x‖≥1，K(x)=0，其中‖‖u表示欧氏范数.

对 ∀x1,x2∈R，有|K(x1)-K(x2)|≤C|x1-x2|，

A5.假设严格平稳过程{(Xti,Yi),i=1, …,n}是绝对规则的，即当j→∞ ，β(j)=，其中是由进 一 步 假 设 ，，其中δ的要求与A1一致，同时我们约定00=0.

A6.对于λ∈(0, 1/2)，k∈[nλ,n1-λ]，且 Λ=[nλ,n1-λ].设Wj= ∫ujK(u)du和Vj= ∫ujK2(u)du.设表示CVL(k)的主要部分，并且忽略高阶无穷小项，则有其中和

D2=4V0∫p(x)σ4(x)M(x)dx.设kL，0=，那么其中

A7.假设函数K(z)=K(‖z‖)存在m阶可导.

假设A7表示权函数是充分光滑，从而应用Taylor公式获得的收敛速度，即

定理3在假设A1～A7下，对于x∈R，且p(x)＞0，当n→∞，则有

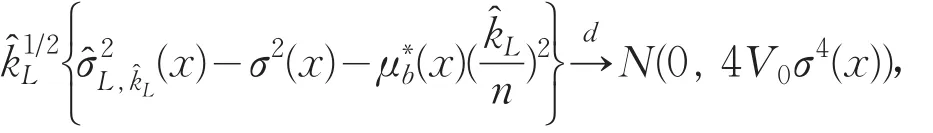
3 主要结论的证明

证明过程中，Xi和x分别表示为Xti和xt.由于漂移项对波动率函数估计量的收敛速度影响是高阶无穷小［2］，因此，假定漂移项是已知的，且这种假设不会影响结论.为证明定理1，引入引理1，即

证明 由公式（6），可知

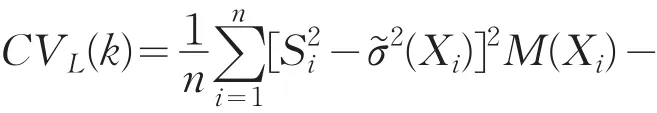
注意到

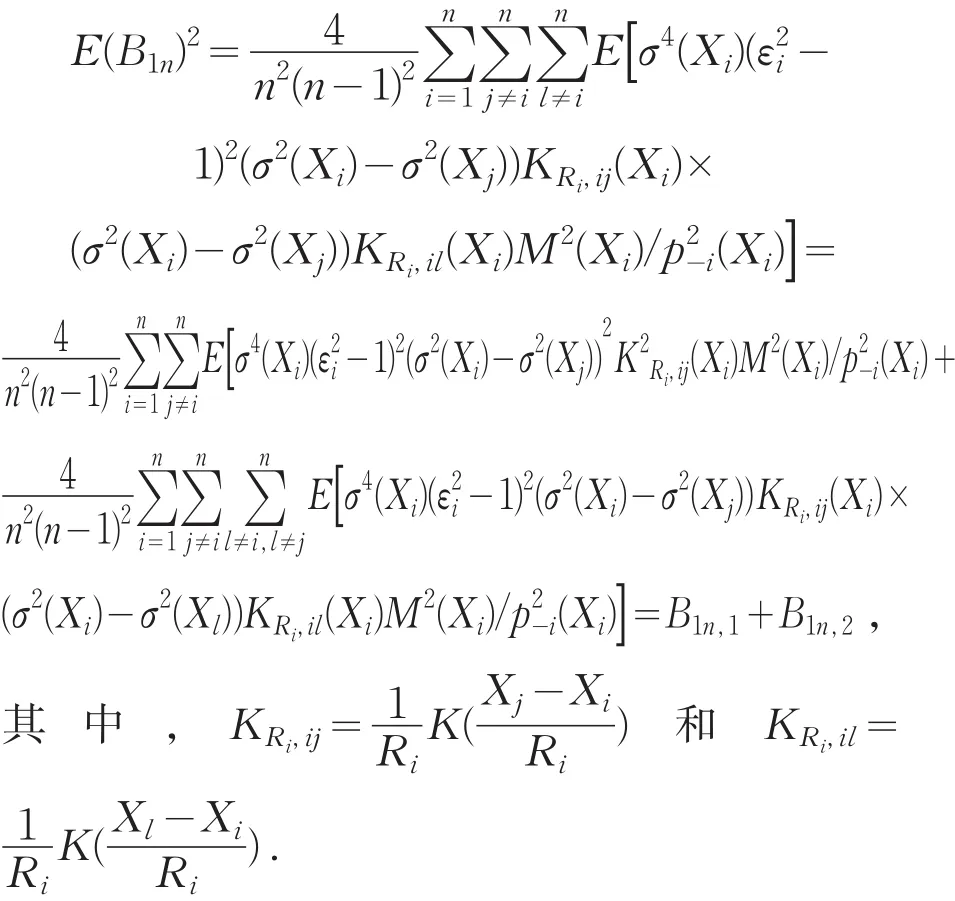
在欧阳德生等人［4］的引理A2下，利用变量变换与Taylor公式可得.于是可得

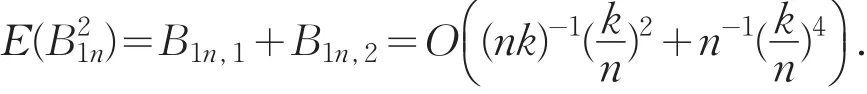
同理可证

因此，B2n=O((nk)-1/2).于是，对于 ∀i，B1i=Op((k/n)2)和B2i=Op((k/n)2).因此，进一步可证得，对于 ∀i，C1i=Op((k/n)2)和C2i=Op((k/n)2).现在考虑

同理可知

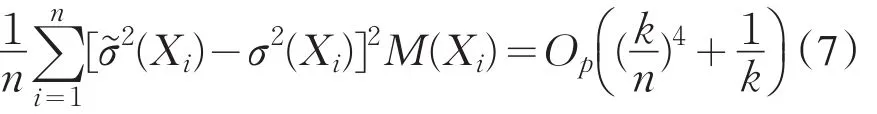
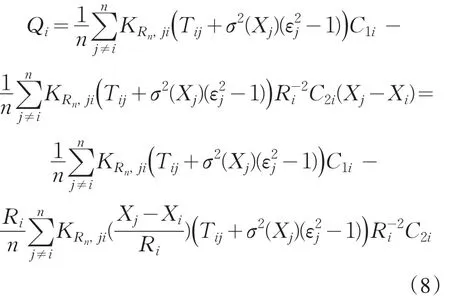
因此，Qi其中有较小的阶，于是，有

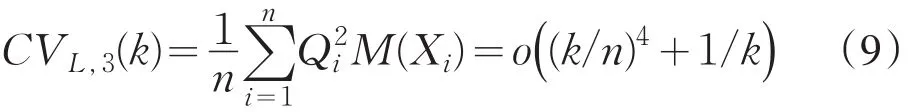
利用Cauchy-Schwarz不等式，结合公式（7），（9），可得

于是可证明

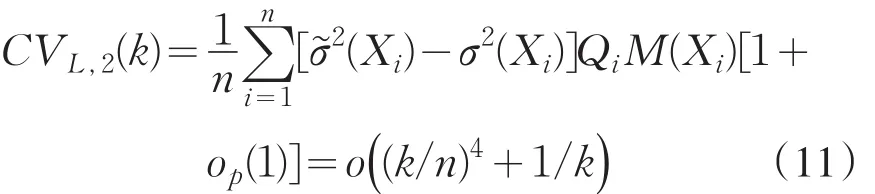
依据公式（9），（10）和（11），可证明引理1.

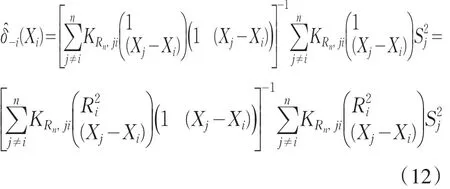
其中，KRi,ji=K((Xj-Xi)/Ri)/Ri.利用 Taylor展开，可得σ2(Xj)=σ2(Xi)+(Xj-Xi)σ˙2(Xi)+Tij，其中，Tij=σ2(Xj)-σ2(Xi)+(Xj-Xi)σ˙2(Xi).

因此

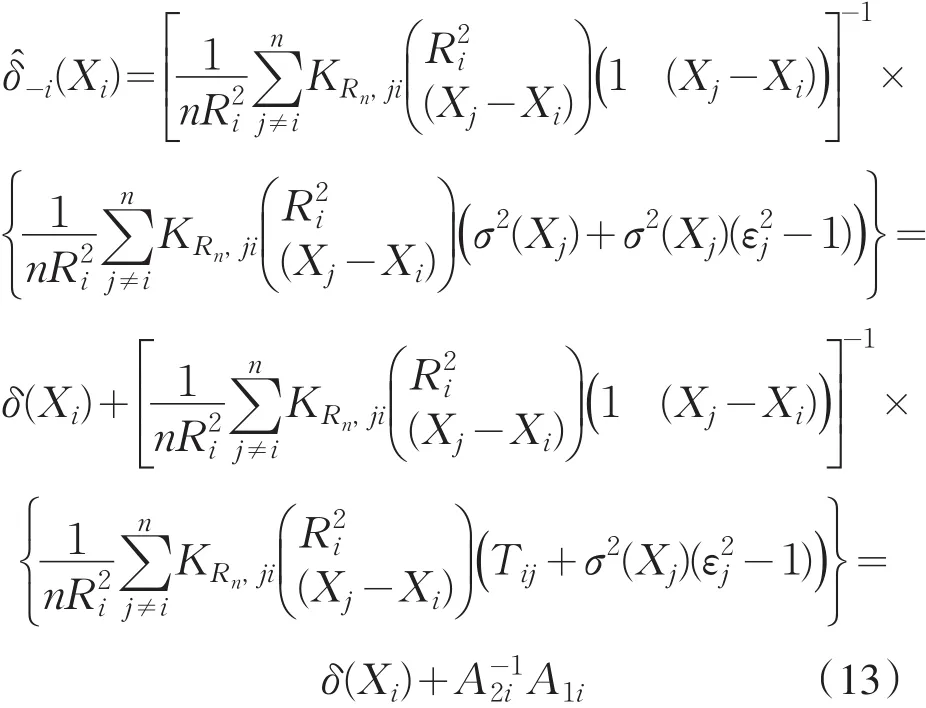
注意A2i的逆为从 而其 中 ，

因此

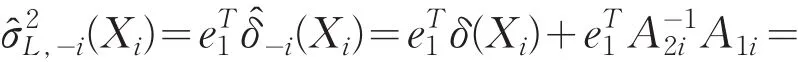
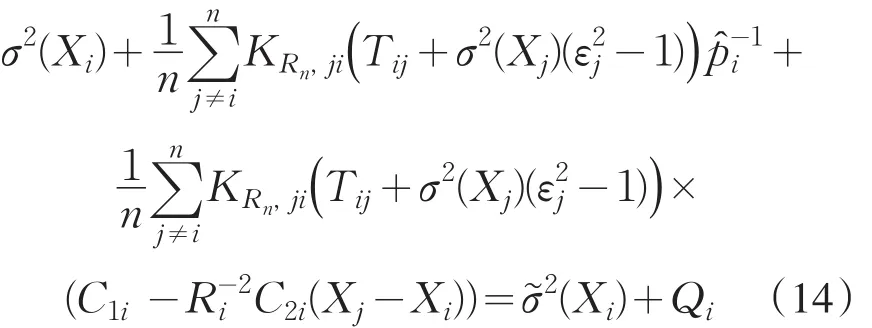
将公式（14）代入CVL(k)，可得CVL(k)=

在引理1下，可知CVL(k)的主要部分为CVL，1(k)，其中其 中注 意CV‴L,1(k)是与k无关的项.

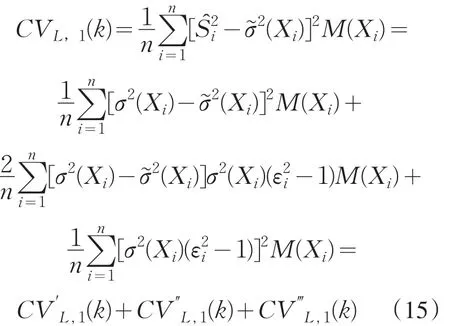
因此，类似欧阳德生等人［4］的定理1的证明，可证得CV″L,1(k)比CV′L,1(k)有更小的阶，且根据公式（7），可知CV″L,1(k)=o(1/k+(k/n)4).因此，CVL,1(k)的主要部分为，即

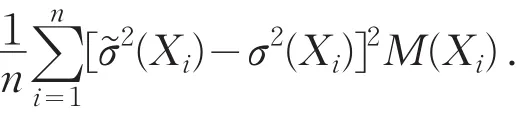
定理2的证明：在定理1中，可知CVL(k)=，其中是不含有k的函数.在定理1的证明中，可知同理，类似于欧阳德生等人［4］的引理A4证明可知，CV2(k)=所以

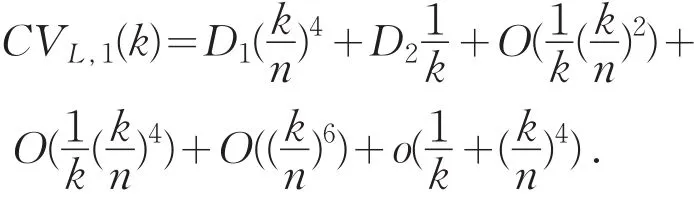
因为 (k/n)4～k-1.因此，n-1(k/n)2～(nk)-1/2，并且于是，

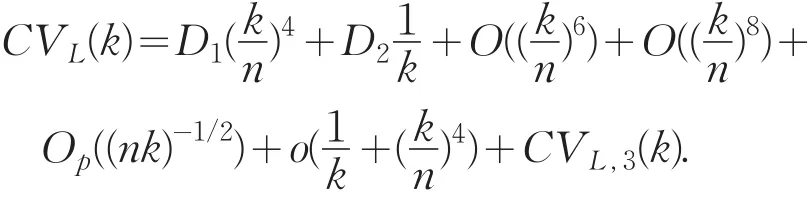
现在来比较 (k/n)6与 (nk)-1/2的价.因为k-1，于是需要比较(k/n)2与(k/n)12或等价于比较2与1 2.显然，(nk)-1/2的阶比(k/n)6的大.定义，则利用Racine和Li（2004）的定理 2.2［5］证明思路，可证得因此

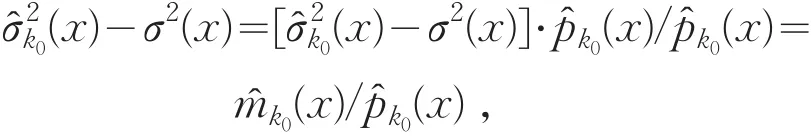
同理，基于定理1的证明，可得

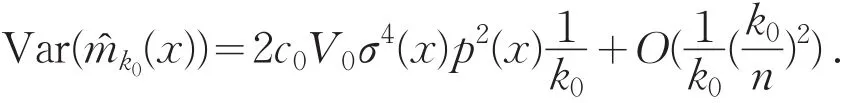
在Lyapunov中心极限定理下，可知

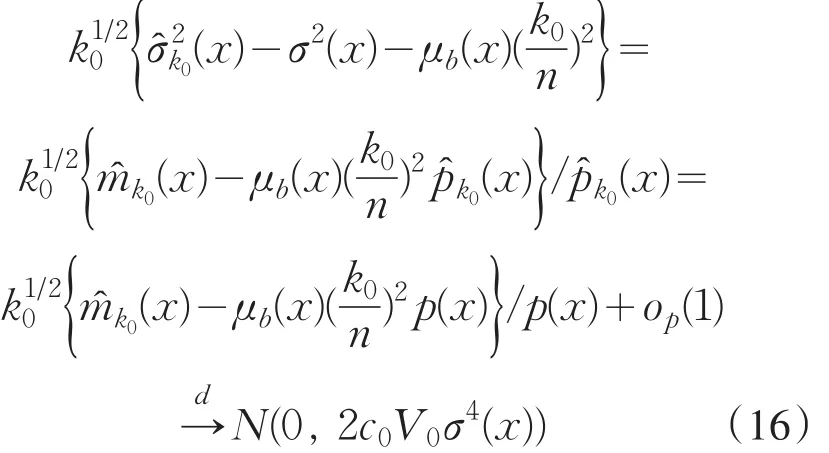
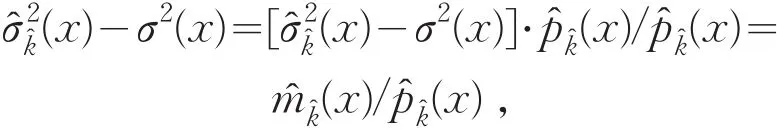
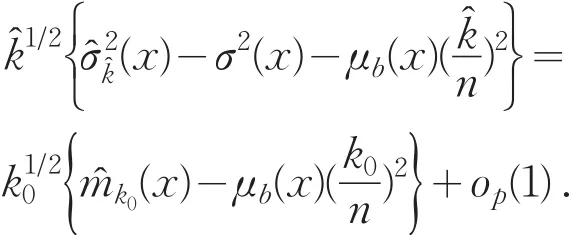
类似上述证明，首先定义

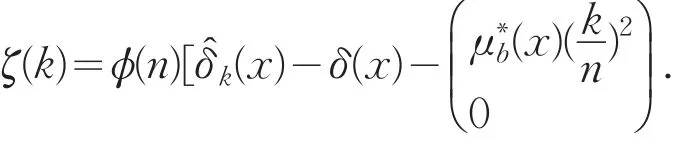
根据欧阳德生等人的定理6，即可证明渐近收敛一个2维正态随机变量.

当 k=kL,0时，易得估计量的渐近正态性，即在中心极限定理下