ANA序列的完全收敛性及强大数定律

何其慧

完全收敛性是概率极限理论中非常重要的一个研究领域，在统计推断中也有很重要的应用.其概念最早由Hsu和Robbins（1947年）提出：称随机变量序列完全收敛于一个常数C，如果对任意的ε＞0，都有ε)＜∞.

由B-C引理可知，上式可以推出在几乎处处（a.s.）意义下Xn→C.自文献［1］提出并建立完全收敛性的结果以来，很多学者对其进行了推广和改进，其中最重要的一个推广结果就是由文献［2］建立的Baum-Katz定理.许多学者将这一结果由独立序列推广到各种相依序列［3-6］.最近，文献［7］又将这个结果推广到单下标加权的渐近负相协（ANA）序列.

由于在很多统计模型中，估计量都是双下标加权的形式，而文献［7］中的结果只考虑了单下标加权随机变量的完全收敛性，因此其实用性非常有限.故本文进一步考虑了双下标加权随机变量的完全收敛性，且本文主要结果的条件较文献［7］的结果都有所改进.

本文引用如下一些记号：C代表正的常数，在不同的地方可以取不同的值，I(A)为事件A的示性函数，a+=aI(a≥0)且a-=-aI(a＜0).

1 预备知识

首先，回顾一下由文献［8］提出的一类相对比较宽泛的相依结构——渐近负相协（ANA）的概念，其定义如下：

定义1定义混合系数

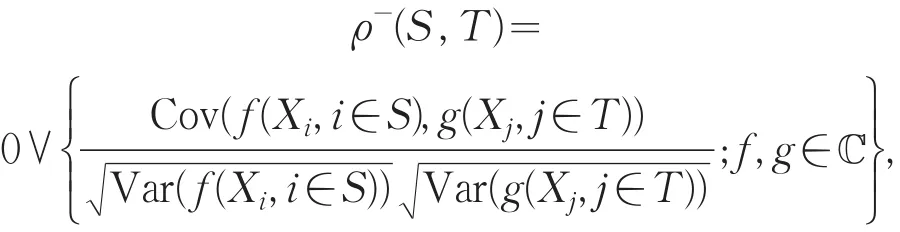
其中，ℂ是非降函数的集合.若混合系数

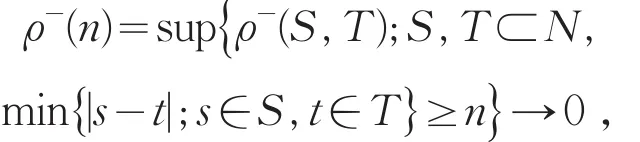
下面介绍随机控制的概念.

定义2若存在常数C，使得对所有的x≥0及n≥1，都有，则称随机变量序列{ }Xn,n≥1被随机变量X随机控制.

为证明主要结果，还需要下述几个引理.

引理1［8］设随机变量 { }

Xn,n≥1为ANA的.若{ }

fn(·),n≥1为单调非降（或非增）函数序列，那么{ }

fn(Xn),n≥1仍为ANA的，且其控制系数不大于ρ-(n).

引理 2［11］令，假设为均值为0的ANA随机序列，满足EXn2＜∞及存在N使ρ-(N)≤s.则存在常数C=C(2,N,s)使得

利用文献［12］中定理2.1的方法，我们可以得到如下的重要引理.

引理4假设{ }Xn,n≥1是被随机变量X随机控制的随机序列，则对任意的a＞0,b＞0以及n≥1，都有

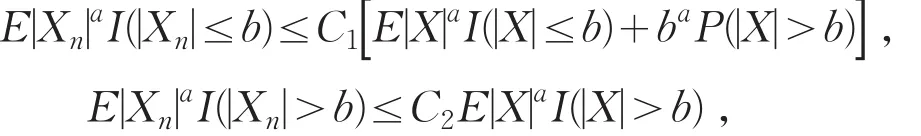
其中，C1和C2代表着不同的正常数.

2 主要结果

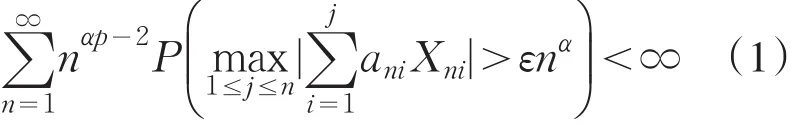
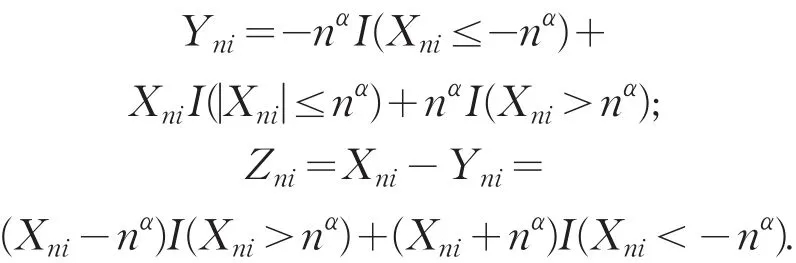
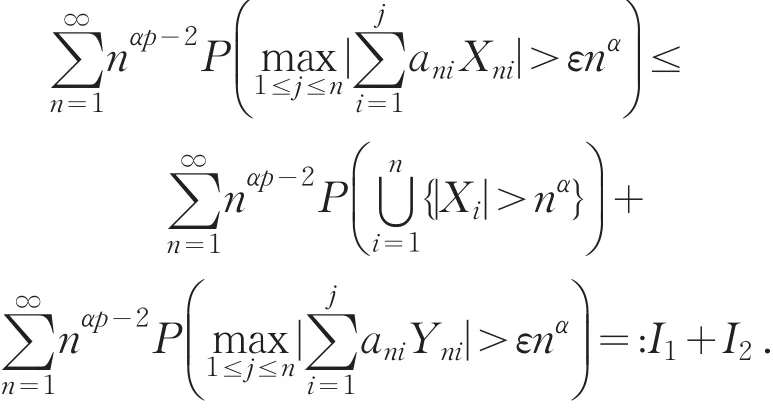
由随机控制的定义容易验证

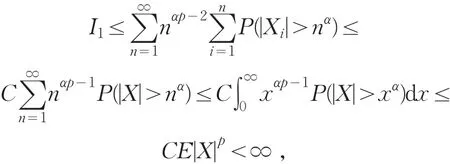
对I2，若0＜p＜1，取μ=min{ }q,1 ，由Markov不等式及引理4可知

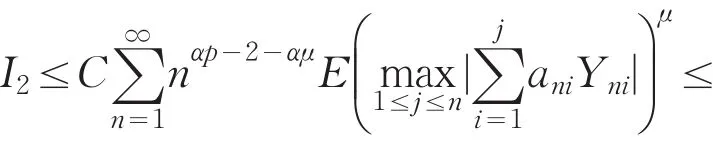
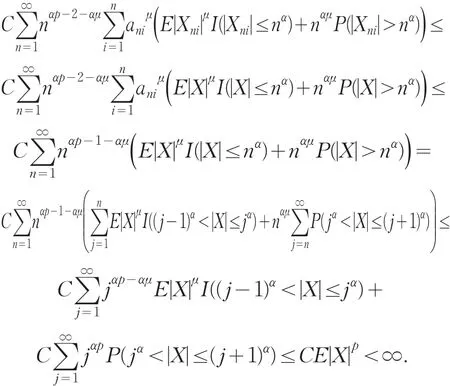
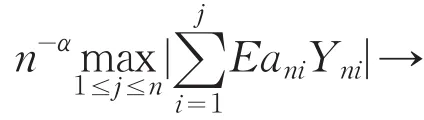
若 1≤p＜2，先证明0,n→∞.事 实 上 ，由EXni=0，αp＞1及E|X|p＜∞可得

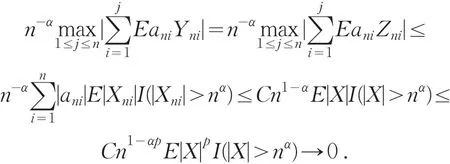
从而当n充分大时，对任意的ε＞0，都有

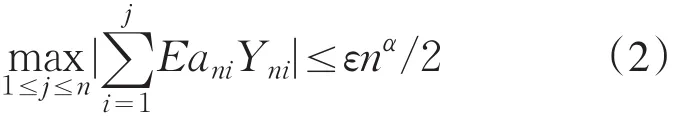
取ν=min{ }q,2 ，由（2）式、Markov不等式、引理3、引理4、Cr不等式及Jensen不等式，可得

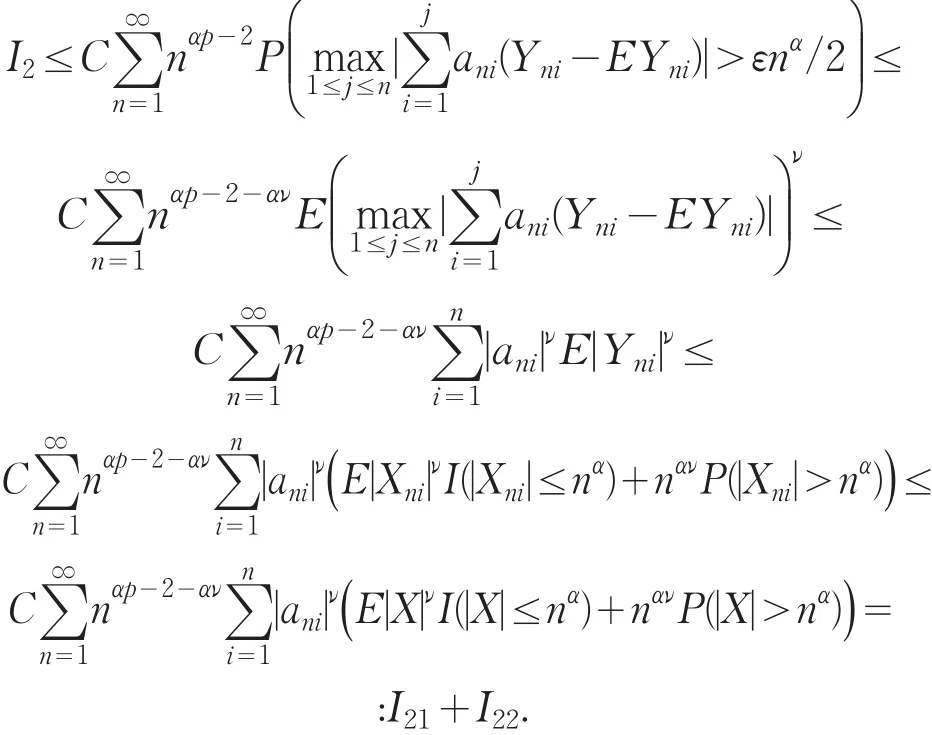
易证

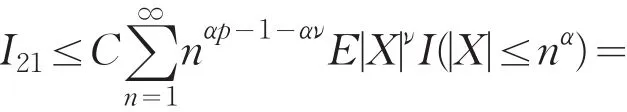
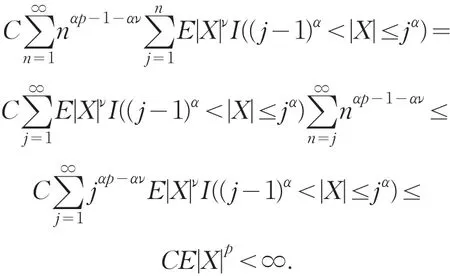
类似可以验证

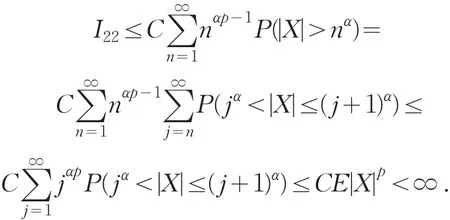
定理2 令 0＜p＜2及i≤n, }

n≥1为一被随机变量X随机控制的ANA随机变量阵列，满足控制系数ρ-(n)≤s.若1≤p＜2则假设对所有 1≤i≤n,n≥1都有EXni=0.令{ }ani,1≤i≤n,n≥1为一满足的常数阵列，其中q＞p.若也被改进到.因此，定理1改进了文献［7］中相应的结果.

文献［7］的结果考虑的是单下标情形下的完全收敛性，而本文的结果定理1则是建立在双下标随机变量和双下标权函数的情形下的，因此具有更广泛的适用性.另外文献［7］中的条件E|X|p＜∞，则对任意的ε＞0，都有

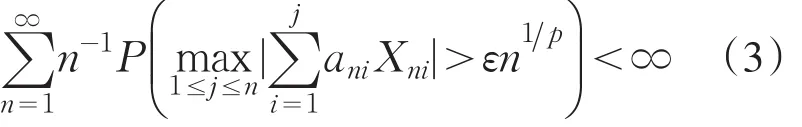
证明 在定理1的证明中取α=1/p，仅需验证在αp=1的条件下也有（2）成立.事实上，由EXni=0，E|X|p＜∞及控制收敛定理同样可得即（2）式成立.其他证明完全类似定理1的证明.此处省略.

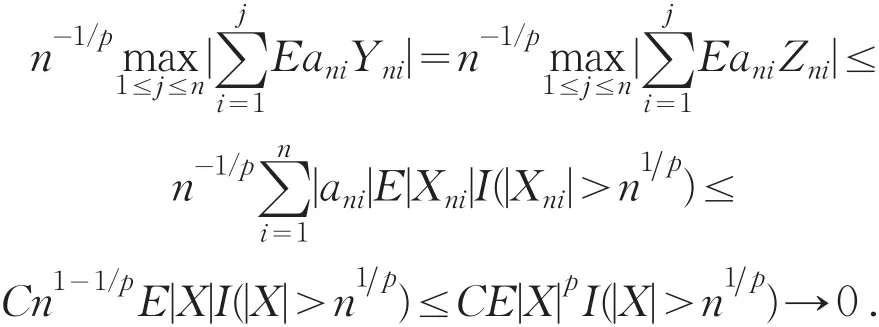
文献［7］也建立了类似定理2的单下标的结果，除了注1中所述的这些改进之外，文献［7］只考虑了1≤p＜2的情况，而定理2更考虑了0＜p＜1的情况.因此，定理2也改进了文献［7］中相应的结果.

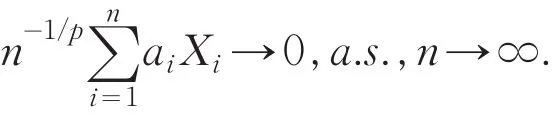
证明 在定理2中取ani=ai,Xni=Xi，可得

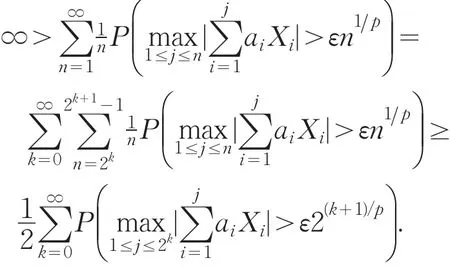
从而由Borel-Cantelli引理，可得

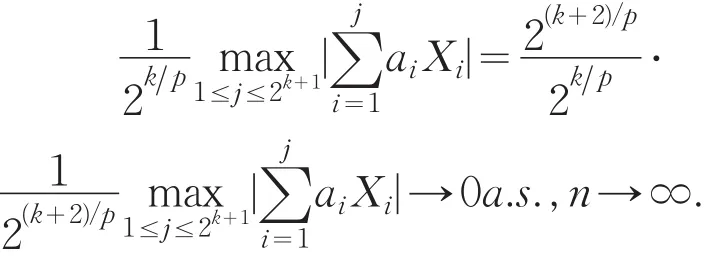
因对任意的n≥1，总存在k使得2k≤n＜2k+1，故而有

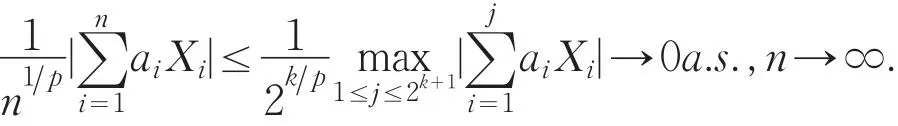
3 结论

本文主要利用关于ANA序列的改良过的矩不等式（见引理4），对双下标加权ANA随机变量加权和的完全收敛性进行了研究，其结果改进了文献［7］相应的结果.作为应用，我们还得到了ANA序列加权和形式的强大数定律.在今后的工作中，我们会进一步将所得结果应用到统计模型中去，为统计研究的发展提供扎实的理论基础.