论数学学习智慧

陈静

【摘要】智慧是人脑最奇妙的产物，智慧的内核首先是道德，并指向于德行与能力完美结合至善至美的境地。数学学习智慧是个体在面临复杂数学情境，解决实际问题过程中表现出来的综合能力，是德行修养、聪明才智、意志品格、计策谋略的综合呈现。因此，数学学习智慧也是数学核心素养的另一种表达。培养数学学习智慧，主要有以下三个途径：一是以”思”提升觉知世界的智慧;二是以”悟”培养认知自我的智慧;三是以”达”形成融会贯通的智慧。

【关键词】核心素养 学习智慧 数学学习

从古至今，人类从未停止过探索智慧的脚步。在东方古老的佛教文化中，智慧一词译为“般若”（梵语），指认知一切事物和万物本源的终极智慧;在西方文化中，智慧则与哲学有关，哲学就是“爱智慧”;在众多哲人眼中，智慧更有着不同的面孔，如苏格拉底认为“德行就是智慧”，柏拉图认为“智慧就是使人完善者”。现代科学则认为，智慧是生命所具有的基于生理和心理器官的一种高级创造思维能力，与个体先天的智力因素有关，但更多的是经过后天实践习得，因此，学习是培养个体拥有智慧的必经之路，正如怀特海在《教育的目的》中所言：“智慧并不一定总是随着知识的增长而增长，只有当我们学会了积极地创造和运用知识的时候，我们才最终拥有了智慧。”

学习智慧即关于学习的智慧，是个体在学习过程中所展现的综合能力乃至创造能力。从数学学科的角度来说，数学学习智慧是学习者在面临数学情境，解决复杂问题过程中表现出来的综合能力，是个体德行修养、意志品格、聪明才智、决策能力等创新意识、创造能力的综合呈现，不仅反映了个体品性与能力的完美结合，也从另一个角度诠释了学科必备品格和关键能力的和谐统一，正如成尚荣先生所言：“核心素养是智慧的合金，智慧是核心素养的中国表达。”培养学生数学学习智慧，正是要求我们关注学习个体在学习过程中的方法、策略、意识等，用智慧的方式去获取知识，培育能力，提升素养。

  一、“思”——觉知世界的智慧

“教育的全部目的就是使人具有活跃的智慧。”（怀特海）学习将促进个体智慧的发展和生成，因此，不仅应该“智慧地教”，更要“智慧地学”。学习智慧是一种学习能力、学习策略甚至技巧，是个体面临陌生情境时显现出来的综合素养，表现为个体对复杂情境做出的分析、判断、选择、评估，乃至解决问题的能力和创造。从这个层面上定义，学习智慧不仅是个体良好学习品质和关键能力的和谐统一，也是学习者自身核心素养的一种综合表达。数学是一门思维性极强的学科，是一门通过思维觉知世界，把握事物之间的数量关系与空间形式的科学。因此，数学学习智慧就是思考的智慧、思维的智慧、思想的智慧，培养数学学习智慧就是要学会用“数学的眼光观察世界、用数学的思维思考世界、用数学的语言表达世界”。

1.敏锐的洞察——寻找与世界的联接

“三个苹果”，改变了世界。夏娃因为好奇吃下第一个苹果，从而创造了人类世界;牛顿被树上掉下的第二个苹果砸中，从而发现了万有引力;而乔布斯发明的第三个苹果更开启了人类物质科技文明的新时代。纵观历史发展的脚步，每一个发明与创造都离不开人类敏锐的洞察力，通过观察产生思考从而把握世界。教学同样需要培养学生敏锐的洞察力，“学会用数学的眼光观察世界”，通过智慧地观察，把握数学与世界的联系。

前不久，听到一节很有意思的数学拓展课：《“肯德基”定价的秘密》。上课伊始，教师首先抛出一个话题：“假设有A、B、C三名同学，他们都想购买一个香辣鸡腿堡，但他们愿意支付的最高价格却各不相同。现在假定三人的最高出价分别是12元、11元、10元。同时，假定每个香辣鸡腿堡的成本都是5元。为了追求利润的最大化，老板该如何定价？”顺势引发讨论交流：商品定价与什么因素有关？在学生热烈的交流中，教师不失时机、循序渐进地介绍一些经济学术语，如“双赢策略” “最高心理价位”“价格歧视”“统一定价”“差异定价”等，帮助学生寻找商品定价背后的秘密，并鼓励学生用数学知识剖析“第二杯半价”“清仓甩卖”“满减满赠”等商业现象，发现其中隐藏的数学奥秘。

这节课除了教学内容的创新，还有学习方式的转变，非常突出的亮点就是用真实问题激起主动探究的欲望，促使学生用数学的眼光看待常见却蕴含着丰富数学元素的生活现象，并通过合作、讨论、汇报、交流等师生、生生互动的学习方式促进学生数学理解的不断深入。一个“有价值”的问题，激发了儿童强烈的好奇心和旺盛的求知欲;一种“有意义”的学习，传递了一个声音——数学教学，除了学习知识，更要培养让儿童适应未来的学习智慧。作为有责任心的教师，我们必须在复杂多变的现实世界中努力培养学生的好奇心，激发求知欲，培养敏锐的洞察力，引导学生积极追寻有价值的数学学习。

2.深刻地把握——關系、结构与本质

数学是抽象性极强的一门学科，从理念层面上理解，数学学科所研究的对象都是抽象思维的产物，是一切存于“理念世界”中的概念，举例来说，我们研究直线，但是在现实世界中并不存在真正的直线，因为除了“直”这个特征，“有长无宽无厚”和“无限延伸”的性质在现实世界中是无法呈现的。因此，完美的直线只存在于数学的理念世界中。但即使有了这样的客观认识，却并不妨碍我们去研究它，我们依然可以通过画出现实中“不完美的直线”来帮助我们研究并理解“理想的直线”的概念和性质，这便是数学思维的独特性。鉴于此，数学学习智慧的重要内涵是学会思维——“会用数学的思维思考世界”。

现实世界变化万千，然而拥有数学学习智慧的人，除了善于观察事物本身，更善于把握事物之间的关系、结构和本质。例如，测量金字塔高度这么复杂的问题，在古希腊几何学家泰勒斯看来，只需要在阳光照射下，找到人的身高与影长相等的这个时刻，便能通过测出金字塔的影长算出其高度;再如，著名的数学家欧拉，把百年未解的格尼斯堡“七桥问题”抽象成简单的一笔画问题，就轻而易举地解决了。虽然，上述两个例子列举的都是举世闻名的数学天才，但即使是普通学习者，只要在学习过程中注意培养，同样可以拥有把握事物内在联系的学习智慧。例如，在数学教学中，讲授抽象概念总需要从一些典型的具体问题出发引入，否则缺少了感性经验的支撑，理解抽象概念本身便会成为“空中楼阁”。然而，实例仅仅是理解抽象概念的基础，真正掌握抽象概念还需要进一步摆脱感性认知经验的局限和干扰，从理性的高度帮助学生构建掌握抽象思维的学习智慧，自觉实现在具体事物层面和理性抽象层面的自由转化，从而培养学生善于把握事物内在关系、结构、本质的高层次抽象思维能力。

3.理性的表达——倾听、对话与分享

数学学习智慧来源于学习过程中的实践体验，是个体运用知识、能力在解决实际问题中通过不断尝试、练习后获得的一种高层次思维能力。这种能力是良好意志品质和能力素养的综合统一体，是促使个体产生创新思想的思维能力，这种能力的形成不可能一蹴而就，而是一个循序渐进不断发展的动态过程。

加德纳的多元智力理论指出，人类个体智力具有多元性和差异性，正是这样的多元差异让每个学习者拥有各自的优势智力和弱势智力，正如一千个讀者就会感知一千个哈姆雷特一样，每个学习者感知周围事物和建构知识的方式、行为各不相同，就会形成个性化的学习智慧。因此，在教学过程中，教师要有意识地引导学生充分进行交流，通过倾听与对话，充分分享彼此的数学理解、体验感悟，进而促进学习智慧的提升。

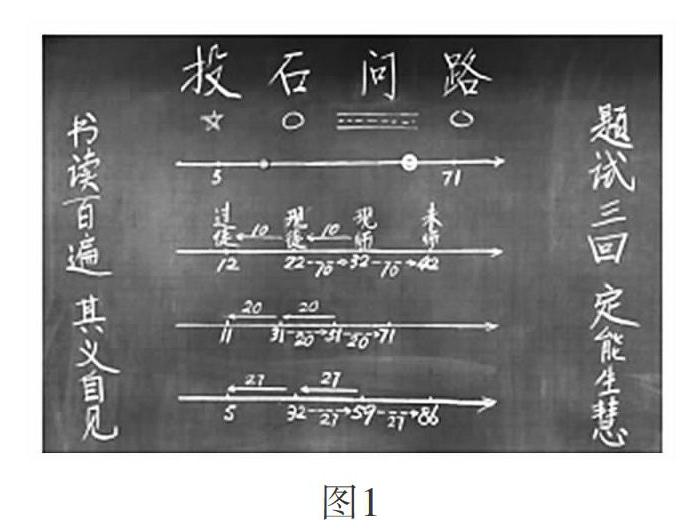
前不久，看见华应龙老师执教的教学课例——《我不是笨小孩——以“师徒年龄问题为例”》，问题源自师徒俩的一段对话：“徒弟：师父您多大了？师父：我在你这年纪时，你才5岁;但是你到我这年纪后，我就71岁了！请问：徒弟几岁？师父几岁？”华老师通过两个教学环节引导学生充分交流表达，探索不同的解题思路，尝试不同的解决办法，并充分引导学生思维的分享、碰撞和融合。环节一：“书读百遍，其义自见”。此环节分三步走，第一步让每个学生充分读懂题目，第二步让学生在读懂的基础上尝试举例说明自己如何理解题意，第三步注意倾听并尝试去理解别人的想法;环节二：“题试三回，定能生慧”。华老师提示学生，用“投石问路”的方式想办法解决问题，在这个环节中，学生充分展示了不同的想法和思考，有的用磁珠摆一摆，用直观图的方式呈现;有的尝试用线段图抽象表示数量关系;还有的用假设法、尝试法、列举法展开思考，在相互交流中分享思考碰撞智慧。（如图1）。

课堂中，华老师引导学生充分地表达、交流，不断激起数学思维的碰撞与交锋，课堂讨论高潮迭起，学习智慧不断闪现，真正体现用教学智慧点燃儿童数学学习智慧。数学学习本来就是不断尝试、实践、体悟、提升的过程，让儿童尝试用符号、语言、数字、图形、表格等不同的形式把握数量之间的复杂关系，通过对话、交流分享彼此的数学理解，这不正是促进数学学习智慧生长的最佳途径吗？

  二、“悟”——认识自我的智慧

学习本身就是一种智慧。

“学，觉悟也”（《说文》），“学”的内涵，侧重于“悟”，注重个体对学习内容和学习方法的领会、思考和体悟，学的过程即是个体自我觉悟、内省而获取知识、经验的自觉行为。中国儒家文化中，把智（慧）与“德”（仁道）紧密联系，认为智慧是良好的道德品行与实践行为的高度统一;现代认识心理学则把人对自我认知和了解能力，称为“元认知”能力，元认知就是一种指向于自我的认识过程，具有较强元认知能力的人，往往具有较强的自我意识和自我监控能力。因此，学习智慧首先要培养人对自我的认识和觉悟，通过自我认知进行自我管理、自我监控和自我调节。

1.学会自我管理：从自觉到自律

虽然影响学习效果的因素有很多，但起决定性作用的因素往往是非智力因素，如兴趣、习惯、态度等，这些优秀的学习品质交织在一起，就形成了学习者自觉、自律的自我约束能力，促使学习者在学习的过程中不断认识自己，努力完善自己，提升学习智慧，并乐此不疲。

从小学阶段开始，学习智慧的差异就已经形成，有的学生善于阅读，从阅读中享受到极大的乐趣，而有的学生却沉溺于智能手机或平板电脑。殊不知，这样潜移默化的习惯养成往往造成学生在自我管理上的巨大差别，自我管理能力强的学生具有较强的自觉性，有时间意识，能对自己的学习活动进行有效的规划和安排，合理分配、统筹兼顾、提高效率，因此能较好地协调学习和休息的关系，从而进入学习的良性循环轨道，而正因为良性循环，让这些学生品尝自觉、自律的乐趣和甜头，寻找最佳的学习方式、方法，愿意努力去尝试更高层次的自我管理，这个过程中学习智慧便自然而然地产生了。

2.学会自我监控：从内省到反思

古希腊著名哲学家苏格拉底曾运用“产婆术”引导学生产生认知矛盾，从而意识到自我的无知，促使学生通过内省引发新的认识，产生智慧。可见，内省与人的智慧相关，是学习者内心认识、省察、反观自我的过程，儒家文化很注重这种内心的道德修养，现代心理学更是将“内省”作为基本研究方法，强调通过内省进行自我监控，从而使自身达到最佳状态或最优效果，从数学角度看，内省更是一种智慧的学习方法和策略，从自我观察到自我分析，从自我分析到自我监控，从自我监控走向自我反思，是一种学思结合的学习智慧之道。

数学学习的自我监控通常要经历这样几个过程：

（1）计划。面临一项学习任务时，首先明确学习内容，获取数学信息，调动已有知识储备，规划可能的解题路径等。

（2）组织。学习过程中，用恰当的方式组织信息，用多元的方式表征数量关系，选择合适的解决方法，明确解题步骤的意图等。

（3）检验。用恰当的方法验证学习过程和结果，回顾解题过程，归纳解题策略， 比较、优化、提炼最佳解题方案。

（4）评价。对学习过程进行自我评价，理性分析学习的质量和效果。

3.学会自我调节：选择与决策

中国传统文化中把认识并处理好人与世界万物关系的能力看作智慧，例如：孔子推崇“中庸之道”，认为智慧的核心是平衡与选择，可见智慧不仅是一种思维方式，也是为人处世、处理问题的方式，智慧本身就包含着选择，这种选择其实是一种自我调节能力，也表现为一种明智决策和合理选择的能力，当个体在现实情境中面对真实问题的时候，能够正确分析、合理判断、正确选择、灵活调节，展示出情感态度、意志品质、能力水平的完美统一，这便是从实践中产生的学习智慧。例如：在遇到复杂数学问题时，及时调整解题思路，合理选择解题策略，或尝试利用具体事例帮助理解，或重新梳理已知、未知条件，分析数量关系;或从复杂问题往后退，退回到简单情况再进行分析等，这些都是学习过程中善于自我调节的数学学习智慧。

  三、“达”——融会贯通的智慧

“达”，本是形容词，意指大道通行无阻，后引申为动词，指相通、相汇之意。数学是一门智慧的学科，数学的学科特征决定了数学与思维的不解之缘。数学是思维的工具，思维是数学学习的基石。数学思维的发展是一个循序渐进的过程，需要持续培养，更要注意方式方法，所谓“一通百通”，唯有善于掌握结构，把握规律，沟通联系，方能达到通达敞亮且融会贯通的境界。

1.举一反三与举三反一

数学学习离不开对关系和规律的把握，发展思维就是要培养学生善于举例，善于类推，善于由此及彼，不仅能举一反三还能举三反一的学习智慧。以数学概念教学为例：概念本身具有一定抽象性，概念的建构过程通常要经历从感性经验积累形成表象，剥离非本质属性，抽象本质属性的过程，在此过程中，通过举例建构学生自己的数学理解至关重要。储冬生老师曾经执教过《认识负数》这节课，储老师让学生通过不同形式的举例，不断加深对负数概念的认识。

（1）“举一反三”。课始，老师通过学生充分交流，了解到学生对负数已经有了一定的认识，于是老师抛出一个问题：“既然你们都在生活中看见过负数，那么，以‘-2为例，你能举出一个生活中的例子说说‘-2是咋回事儿吗？”

（2）“举三反一”。课中，当学生对负数有了更深的认识后，老师又抛出一个问题：“我们以前认识的数，数字越大这个数就越大，如28比1大，但是负数怎么就是相反的呢？比如-2就大于-13，你能举几个不同的例子说明这个问题吗？”

课中的两次举例都蕴含了丰富的学习智慧。第一次举出生活中不同的事例，以丰富的生活原型来解释“-2”这个抽象的数学模型，从一般到特殊，从具体到抽象，有助于学生对抽象的负数的理解;第二次用不同的例子来佐证-2>-13，从数学模型又回到生活原型，从特殊到一般，在举三反一的类比中加深对抽象概念的理解和认识。

2.自由开放与多元并举

数学学习就是要让学生学会思维。因此，教师在课堂上的主要教学任务就是想方设法地制造认知冲突，激起思维碰撞，在不断经历思维挑战的过程中，引领学生攀登思维的高峰。有高层次思维挑战的课堂是生动的，因为有学生鲜活灵动的思考存在;也是开放的，因为有多种不同思想的碰撞与交锋;也是自由的，这是一种思想上的自由，允许发出不同的声音，更鼓励思辨、质疑与批判。数学教学的视野也不能仅仅局限于一门学科的知识教学，更应该突破教学的围墙，超越学科的边界，引领学生看向更远、更大、更广阔的空间，注重培养学生的自由之思想和独立之精神，在获取知识的过程中，与师生思想的碰撞融合，学习中的喜怒哀乐，想象力、创造力、研究力等独立学习能力之生发，进而学习观、价值观、人生观的形成，这些都将超越知识的范畴，使数学学习的过程最终成为提升素养增长智慧的过程。

  【参考文献】

[1]【英】怀特海.教育的目的[M].徐汝舟译.北京：三联书店，2002.

[2]成尚榮.核心素养的中国表达[M].上海：华东师范大学出版社，2018.

[3]华应龙.我不是笨小孩——以“师徒年龄问题为例”[J].小学数学教师，2018（6）.