对2019年武汉市高三二月调考理科第20题的探究与思考

☉湖北省武汉市第二中学 张鹄

☉湖北省武汉市教育科学研究院 孔 峰

☉湖北省武汉市黄陂区第一中学盘龙校区 李红春

2019年武汉市高中毕业生二月调研测试理科试卷，严格遵照课程标准和考试说明的要求进行命制，体现了“覆盖面广、难易适中、小巧灵活、贴近高考、突出能力”等方面的命题风格.各类题型背景熟悉，载体简单，蕴含丰富，给人以自然、流畅、质朴、和谐的深刻印象.其中理科第20题直线与椭圆的综合问题，命题立意高、构思精巧、蕴含着丰富的高等背景，凸显了射影几何性质初等化的转化思想，考查了学生的数学运算、逻辑推理等数学核心素养能力，其既体现了数学的本质，又让人感受到了命题者的深度思考.为了便于领会命题意图，本文拟从解法推广到背景揭示等方面进行解读，供同仁参考.

一、试题及评析

题目武汉市2019届高中毕业生二月调研测试理科第20题：

（1）求椭圆Γ的标准方程.

（2）过点P（1，0）作直线交椭圆Γ于A，B两点，点Q为平面上一点，直线QA，QB，QP的斜率分别是k1，k2，k0，且k1+k2=2k0.问：点Q是否在某条定直线上运动，若存在，求该直线方程；否则，请说明理由.

试题表述简洁，问题设计层次分明，难易梯度合理，解法灵活多样.第一问属于封闭问题类型，强调基本方法的运用；第二问体现开放问题特征，强化探究运算思路，选择运算方法，彰显了数学运算与逻辑推理在探究和表述论证过程中深度融合的特征.本题的设计目的清晰地表明解析几何的复习备考应重在引导考生掌握基础知识，形成扎实且全面的学科核心素养.

二、变式推广

本题的第二问是整个题目命制的亮点，对它的引申推广就成了水到渠成的过程.经思考，得到如下一些结论：

结论1：过点P（m，0）（m≠0）作直线l：y=k（x-m）与椭圆交于 ，两点，为平面上一动ABQ点，直线QA，QB，QP的斜率分别是k1，k2，k0，且k1+k2=2k0，则点Q的轨迹方程是

证明：设点则

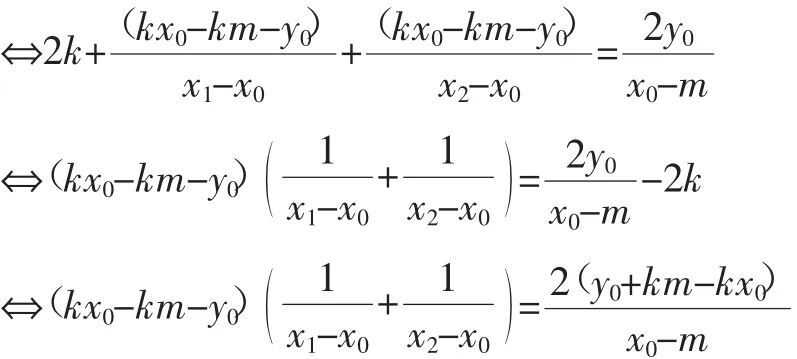
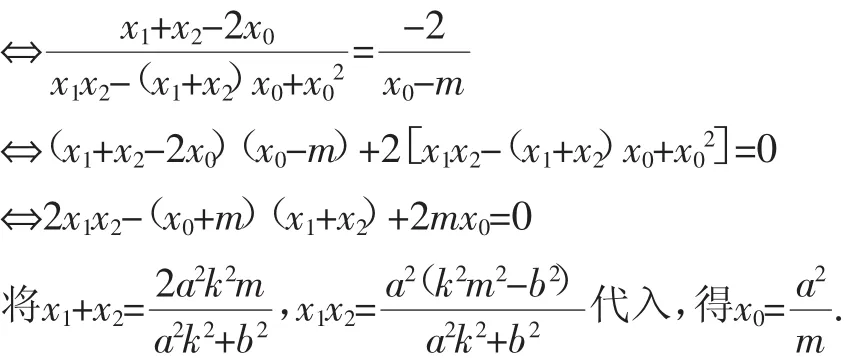
运用上述证明方法易得下面的结论2和3：

结论2：过点P（m，0）（m≠0）作直线l：y=k（x-m）与双曲线交于 ，两点，为平面上一动ABQ点，直线QA，QB，QP的斜率分别是k1，k2，k0，且k1+k2=2k0，

则点Q的轨迹方程是

结论3：过点P（m，0）（m≠0）作直线l：y=k（x-m）与抛物线Γ：y2=2px（p＞0）交于A，B两点，Q为平面上一动点，直线QA，QB，QP的斜率分别是k1，k2，k0，且k1+k2=2k0，则点Q的轨迹方程是x=-m.

三、背景揭示

追踪试题的命题轨迹，探寻试题的命题背景，有助于提升思维高度，开阔视野，促进教师向着更加深刻的专业化发展.

借助调和点列和调和线束等相关概念可以深刻揭示本题的命题思路与背景.作为一名中学数学教师，应当了解这方面的相关知识，以便更好地解答学生的疑问：为什么是这样的结论？进而才能识破题目的神秘面纱，解析试题的内在背景，并最终把握试题的命题规律.

1.射影几何中关于二次曲线的有关概念和定理

定义：如图1所示，设点Q是不在平面二次曲线上的一点，过点Q引两条割线依次交曲线于点E，F，G，H，连接EH，FG，交于点P，连接EG，FH，交于点N，则直线PN为点Q对应的极线.若Q为曲线上的点，则过点Q的切线即为极线.同理，直线QN为点P对应的极线.

图1

定理：（1）当点P为二次曲线Γ上的点时，则点P的极线是二次曲线在点P处的切线；

（2）当点P为二次曲线Γ外的点时，过点P作二次曲线Γ的切线，切点分别为A，B，则点P的极线是直线AB；

（3）当点P为二次曲线Γ内的点时，过点P任作割线交二次曲线Γ于A，B，设曲线Γ在A，B处的切线交于点Q，则点P的极线即为点Q的轨迹.

2.借助高观点思想方法审视试题解题过程

这里不妨假设二次曲线为椭圆，对于其他二次曲线可作类似讨论.

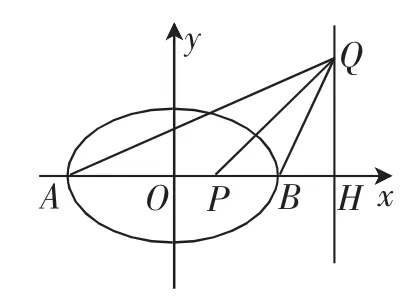
图2

首先，考查特殊情形，当过点P的直线为x轴时，如图2所示，不妨设点Q在第一象限，则

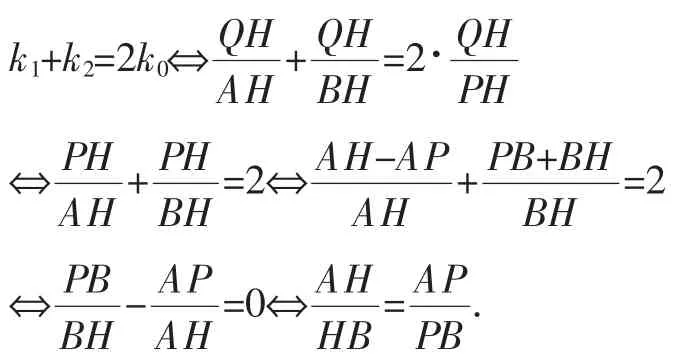
k+k=2k⇔QH+QH=2·QH 120A HB HPH⇔PH+PH=2⇔AH-AP+PB+BH=2 A HB HA H BH⇔PB-AP=0⇔AH=AP.BHA HHBPB

这说明点P，H调和分割线段AB，其分割比为1，因此有

其次，当过点P的直线斜率存在且不等于0时，如图3所示，

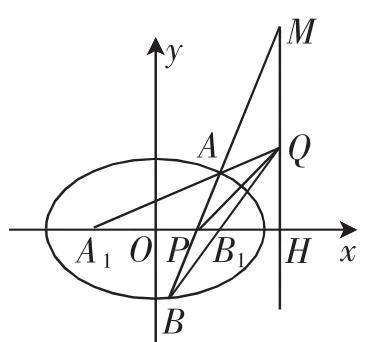
图3

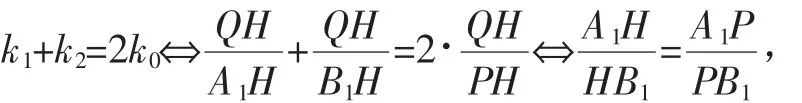
这说明点P，H调和分割线段A1B1，从而分割比为1，同上有

另外，当点P、点Q分别位于焦点和准线与x轴的交点时，即为2018年全国Ⅰ卷理科第20题第二问的情形.

由此可见，此类问题是射影几何中调和点列和调和线束的初等化表现.弄清它们之间的内在联系，有助于我们揭示本质，拓展认识，更有助于我们在教学中举一反三以培养学生的类比思维能力和发散思维能力，提升学生的数学素养.F