由一次习题课教学片断引起的思考
☉江苏省南通市通州区教师发展中心 王惠清
习题课该如何上?这是我们每一位数学老师都应该思考的问题.在一次区级调研活动中,笔者关注到某年轻教师的一堂习题讲授课,现就其在“完美解法”“优秀解法”的教学上作出自己的思考.
师(边板书):前段时间出现了这样一道有关数列方面的考题,今天我们就围绕这一考题进行以下探讨.
题目 在等差数列{an}中,当且仅当n=6时,Sn有最大值,则使Sn>0的n的最大值为______.
师:我们班的52名同学在此题的得分情况上很不乐观:40名同学一分未得;7名同学得了部分分数;5名同学空白未答.
师:借助抛物线的图像来解决此题就显得特别直观且完美了,大家看一下老师的完美解法:
①当对称轴n=5.5时,如图1,由对称性知,S11=S0=0,当对称轴向右微移时有S11>0且S12<0.
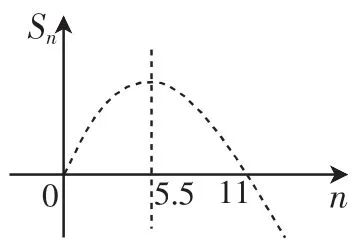
图1

图2
②当对称轴n=6.5时,如图2,由对称性知,S13=S0=0,当对称轴向左微移时有S12>0且S13<0.
综合①②可得,若使Sn>0的n的最大值为11或12.
点评:这是借助二次函数图像解决问题的方法,解题时取两个极端点作为对称轴,并在抛物线的对称轴左移、右移时对图像的变化进行观察,体会出S11>0且S12<0或S12>0且S13<0并得出结论.该班执教老师在课后对学生进行了问卷调查,学生对这一“完美解法”“优秀解法”的掌握情况并未达到教师的预期,很多学生在该方法的理解与接受上表现得很吃力,教师未作铺垫就作出了过原点的图3的情形,教师在这一过程中又是怎样进行思考的呢? 假如首项a1<0,则S1=a1<0,此时的图像很可能即为图4所示的不过原点的情形,假如正是图4所示的情形,那么S11、S12、S13的正、负又该怎样判断呢?教师所展示的这一解法确实直观且准确,但在解题的过程中似乎总有什么环节显得并不那么顺畅.
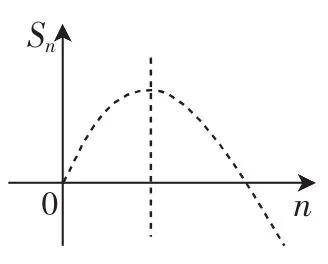
图3

图4
笔者在之后所进行的教研活动中有意识地提及了这一问题,大多数同事在此题的解法上持有相同的想法,很多同事对于此题是否存在更易理解的解法上并未作出深刻的思考.笔者深知该教师的解法确实堪称完美,但该问题背后所隐藏的深层知识并未得到应有的挖掘与思考,于是笔者便对该题中所隐含的深层问题作一次由难到易的探究.
探究1:基于二次函数Sn的图像对对称轴在不同位置上引起的Sn的变化进行观察与分析,并由此得出结论,这是模仿上述“完美解法”作出的思考,但显然更完整.

图5

图6
②当对称轴n′靠近区间(5.5,6.5)的左端点时,由n′=得a>-5d>0,因此S=a>0,又S=0(虚拟值),1110令对称轴n′=5.6,Sn的图像如图6所示,其虚拟零点为n=0和n=11.2,因此S0=S11.2=0,又Sn在区间(5.6,+∞)上单调递减,因此S11>S11.2=0且S12<S11.2=0,所以使Sn>0的n的最大值为11.

图7
③当对称轴n′靠近区间(5.5,6.5)的右端点时,由得首项-5d<a<-6d,则1S1=a1>0,又S0=0(虚拟值),令对称轴n′=6.4,Sn的图像如图7所示,Sn的虚拟零点为n=0和n=12.8,因此S0=S12.8=0,又Sn在区间(6.4,+∞)上单调递减,因此S12>S12.8=0且S13<S12.8=0,所以使Sn>0的n的最大值为12.
综合①②③可知,使Sn>0的n的最大值为11或12.
点评:这一解法相对烦琐,但显然对学生的抽象概括能力、运算能力、思维能力都能起到很好的锻炼作用.
探究2:着眼于对称轴进行分类讨论,根据其位置对Sn的正负变化进行判断.
①当对称轴5.5<n′=k≤6时,有60.5<11k≤66且66<12k≤72,因此S11>0且S12≤0,此时使Sn>0的n的最大值为11;
②当对称轴6<n′=k<6.5时,有72<12k<78且78<13k<84.5,因此S12>0且S13<0,此时使Sn>0的n的最大值为12.
综合①②可知,使Sn>0的n的最大值为11或12.
点评:这一解法虽然比探究1中的解法更为简洁,但对于解题者的思维能力和逻辑推理能力却提出了更高的要求,学生运用此法解题时大多无法达到最终目标.
探究3:着眼于对称轴落实函数解法,构造数列“和”函数,并对“和”函数的性质进行研究,最终通过构造不等式对n的取值范围进行确定.
点评:这是一种思维量、计算量都不大且易于操作的解法,是适合广大学生的主流解法.
探究4:根据题意对数列的正负分界项进行确定可得an>0且an+1≤0(或an≥0且an+1<0),根据等差数列的性质ap+aq=am+an进行等价转换,可得Sn>0且Sn+1≤0(或Sn≥0且Sn+1<0).
分析:当且仅当n=6时,S6取得最大值,则公差d<0,同时a1>0,a2>0,a3>0,a4>0,a5>0,a6>0且a7<0.
①若a6+a7>0时,有且所以S>0的n的最大值为n12;
②若a6+a7≤0时,有且,所以使S>0的n的最大值n为11.
综合①②可知,使Sn>0的n的最大值为11或12.
点评:这一解法更为简洁,但对解题者的知识储备要求较高,如ai>0(i=1,2,3,4,5,6)且a7<0,另外还要求解题者对等差数列性质的等价转换熟练掌握,否则解题就比较困难了.
上述四种探究正好是从四个角度对该题进行解读,探究1实际上是对该执教老师“完美解法”的模仿,只不过相比而言更为深入且全面,问题的本质也在探究1的解读中获得了很好的揭示,学生也更容易接受.探究2则是在探究1解法基础上进行优化,着眼于“和式Sn”并对S11、S12、S13的正负进行了逐步的判断.在探究2的解法上进行优化与整合所得的探究3存在着显著的优点,分步判断的正负得以省略,通过解不等式kdn>0得以锁定自变量n的范围.从探究3的角度出发并借助等差数列的性质,得到了探究4中的解法,这一解法更为新颖.对这四种解法进行比较不难发现,探究3、探究4中的解法相对更为简短,解题书写更为容易且清晰,很多学生也更加倾向于这两种解法.
体会:解决“当n为何值时,使Sn的值最大或最小”或“使Sn>0(Sn<0)的n的值最大或最小为多少”一类问题时,通性通法往往是在“完美解法”不足之处的思考上获得的,对“完美解法”进行去粗存精、整合优化的深入探究往往能够得到更好的解题效果.F

