面朝大海，春暖花开——一道江苏模拟试题的探究

☉江苏省常熟中学 曹正清

圆锥曲线的定值问题一直是高考数学的常见题型之一，也是备受命题者、老师与学生关注的焦点之一，难度一般为中等及中等偏上.圆锥曲线的定值问题充分体现出动与静的完美统一，是解析几何知识的综合与交汇问题，其背景生动，内容丰富，综合性较强，趣味性也较强，充分将函数与解析几何融为一体，要求有较强的综合能力与应变能力，充分考查学生的数学能力与素养.

一、问题呈现

问题（2019届江苏省徐州市高三12月月考）如图1所示，在平面直角坐标系xOy中，过椭圆的左顶点A作直线l，与椭圆C和y轴正半轴分别交于点P，Q.

图1

（1）若AP=PQ，求直线l的斜率；

（2）过原点O作直线l的平行线，与椭圆C交于点M，N，求证：为定值.

本题以椭圆为问题背景，通过巧妙设置以线段长度相等的条件来确定对应的直线斜率，又以平行线的关系来巧妙设置直线MN，通过点P的运动带动点Q与直线MN的运动，进而求证线段的比值为定值.背景简单，立意新颖，思想丰富，知识融合，动静结合，实属难得，具有非常好的学习、观摩、研究、拓展的价值.

二、问题解决

解析：（1）分析1：设出点Q的坐标，利用中点的坐标公式确定点P的坐标，代入椭圆C的方程确定相应的参数值，再利用直线的斜率公式即可求解对应的斜率.

方法1：依题意，椭圆C的左顶点A（-2，0），设Q（0，m）（m＞0），由AP=PQ，可得

代入椭圆

解得（负值舍去）.

所以直线l的斜率为

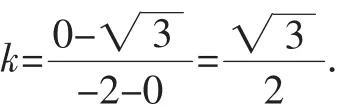
分析2：设出直线l的斜率，进而确定对应的直线方程，并与椭圆C的方程联立，通过二次方程的转化，利用根与系数的关系来确定点P的横坐标xP，利用线段的关系得到xP=-1，进而得以求解对应的斜率.

方法2：依题意，椭圆C的左顶点A（-2，0），

设直线l的斜率为k（k＞0），点P的横坐标为xP，

则直线l的方程为y=k（x+2）， ①

又椭圆

联立①②得（4k2+1）x2+16k2x+16k2-4=0，

则，从而

因为AP=PQ，所以xP=-1，

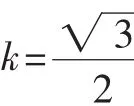
所以，解得（负值舍去）.

（2）分析1：先根据直线l的方程确定点Q的坐标，利用两点间的距离公式确定AQ，通过联立方程组，并借助根与系数的关系，以及弦长公式分别求解AP与MN的值，代入对应的比值关系式并化简即可得以证明.

证法1：设直线l的斜率为k（k＞0），则直线l的方程为y=k（x+2），

令x=0，得y=2k，则Q（0，2k），

可得

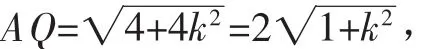
联立方程组消元可得

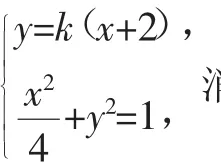
则

可得

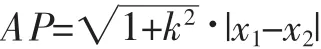
由题可知直线MN的方程为y=kx，

分析2：设出直线l的方程，通过联立方程组，并借助根与系数的关系，结合点A的横坐标得到xP的关系式，同理得到xN的关系式，利用对应的比值关系式所对应的线段长度转化为其在x轴上的射影的对应比值，进而加以化简即可得以证明.

证法2：依题意，椭圆C的左顶点A（-2，0），

设直线l的斜率为k（k＞0），点P的横坐标为xP，

则直线l的方程为y=k（x+2）， ①

联立①②得，（4k2+1）x2+16k2x+16k2-4=0，

设点N的横坐标为xN，则直线MN的方程为y=kx，③

通过取极端位置，以特殊情况来确定一般条件下的定值问题.利用点P与点Q重合的极端位置来加以分析，可以有效减少复杂的计算，得以简单化证明.但在实际解决此类解答题时很少用，可以用来引导思维或者在解决小题时采用.

取极端位置，令P与Q重合，此时Q（0，1），可得AP·AQ=AQ2=4+1=5，

可得直线l的斜率为，直线MN的方程为

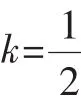
从而，即证.

三、问题探究

探究1：通过改变题目中的椭圆方程为一般形式，可得以下变式

变式1：如图1所示，在平面直角坐标系xOy中，过椭圆的左顶点A作直线l，与椭圆C和y轴正半轴分别交于点P，Q.过原点O作直线l的平行线，与椭圆C交于点M，N，试求证为定值

证明：依题意，椭圆C的左顶点A（-a，0），

设直线l的斜率为k（k＞0），点P的横坐标为xP，

则直线l的方程为y=k（x+a）， ①

令x=0，得y=ka，则Q（0，ka），

联立①②得，（a2k2+b2）x2+2a3k2x+a2（a2k2-b2）=0，

又直线MN的方程为y=kx， ③

四、结论拓展

其实，把相应的椭圆问题深入拓展到圆、双曲线之中，也有类似的结论.

探究2：通过改变题目中的椭圆方程为圆的方程，可得以下结论

结论1：在平面直角坐标系xOy中，过圆C：x2+y2=r2（r＞0）与x轴负半轴的交点A作直线l，与圆C和y轴分别交于点P，Q.过原点O作直线l的平行线，与圆C交于点M，N，则有为定值

具体的推导过程可以结合以上的解析思路加以分析与证明.

探究3：通过改变题目中的椭圆方程为双曲线的方程，可得以下结论

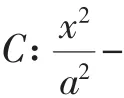
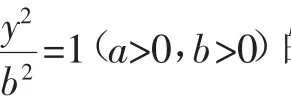
结论2：在平面直角坐标系xOy中，过双曲线的左顶点A作直线l，与双曲线C的另一支和y轴分别交于点P，Q.过原点O作直线l的平行线，与双曲线C的两支分别交于点M，N，则有为定值

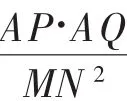
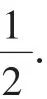
具体的推导过程可以结合以上的解析思路加以分析与证明.

其实，在探究圆锥曲线中的定值问题时，往往可以发现点、直线、圆、圆锥曲线等知识之间的内在联系与规律，从而加强对相关内容的正确理解与掌握，有助于数学解题能力与应用能力的提高，真正达到提升数学能力，拓展数学素养的目的.F