基于变式引申的高中数学探究式教学研究

☉福建省福清华侨中学 俞文锐

在传统的高中数学教学中，为了使学生对数学思想、数学问题的认识和理解统一到基本理论和概念上来，往往将广阔的思路聚焦到同一个焦点上来，然而，这种教学模式很难产生创新性的思想，也会使学生一味地迷信教师、专家、教材等权威，致使学生长期束缚在被动接受、模仿训练等局面上.而基于变式引申的探究式教学则高度重视教材中的每个习题，更加注重学生的发散性思维的发展，鼓励学生通过变式来不断理解并拓展知识，有效地摆脱了思维定式的制约.

一、引入形成变式探究

为了促进知识的迁移，进而建立新旧知识之间的链接，教师应在知识引入时，引导学生从已有的认知结构出发，按照最近发展区理论，充分利用多媒体来展示日常生活中的直观材料，让学生以小组的形式参与探究概念的本质.例如，在讲解异面直线的概念时，笔者运用投影仪向学生呈现了日常生活中的茶几、桌椅等直观材料，并将直观现象的实物图形通过图形变式，来帮助学生理解异面直线的具体特征.

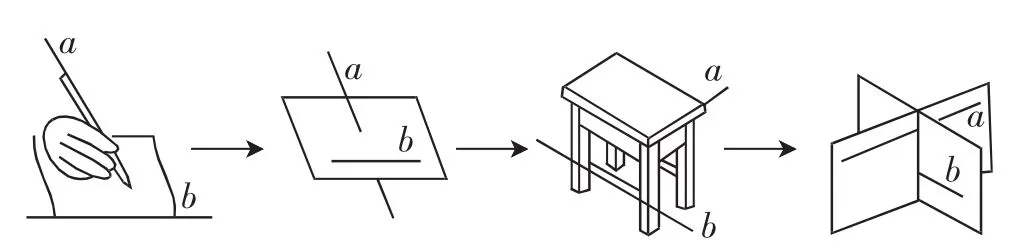
图1 异面直线变式图

二、辨析论证变式探究

为了达到通过观察变化的现象来透析数学知识的实质的目的，教师应引导学生对所呈现的数学命题实施观察与思考，鼓励学生通过转换观察和思考方式，对命题的内涵和外延进行变式，并组织学生再次进行推导与证明，多角度、多方位、多层次的透彻理解概念，达到培养思维深刻性的目的，值得说明的是，在具体实践中，不能急于应用知识去解答问题.例如，在学习棱柱定义后，笔者及时展示了直棱柱、斜棱柱、正棱柱、长方体、正方体等与棱柱相关的概念，同时要求学生总结出长方体、正四棱柱等一系列平行六面体的特点，并在以下相应的横线上增添图形变化要求，进一步了解以下棱柱之间的相互变化关系.

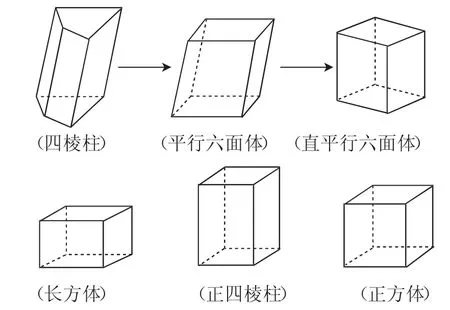
图2 几种棱柱关系图

三、巩固应用变式探究

为了使学生不再停留在原有的表面现象和所学知识上，教师应将所学知识运用到新的变式问题情境之中，充分利用其本质来解答问题，有效地开拓学生的视野.例如，在学习完判断奇偶性的定义后，笔者及时呈现了以下三个变式，要求学生在相互探究的基础上完成以下题目：

变式1：请判断下列函数的奇偶性.

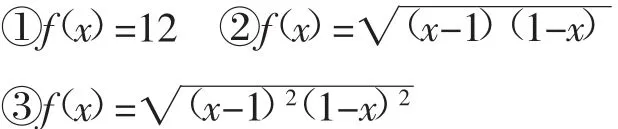
设置目的：设置以上三个特殊函数，有效巩固学生运用定义判断函数奇偶性的知识.

变式2：以下说法正确吗？请说明你的判断理由.

①若f（x）的图像关于y轴对称，则f（x）一定是偶函数.

②若f（x）是偶函数，则f（x）的定义域一定关于坐标原点对称.

③若f（x）的定义域关于坐标原点对称，则f（x）一定是偶函数.

设置目的：变具体函数为抽象函数，深刻体会从特殊到一般的思想.

变式3：请根据图形解题.

①偶函数y=f（x）的局部图像如图3所示，则f（-4）等于多少？

②偶函数y=f（x）的局部图像如图4所示，请判断f（1）与f（3）之间的大小关系.

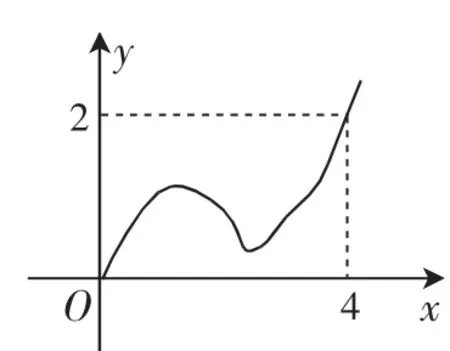
图3

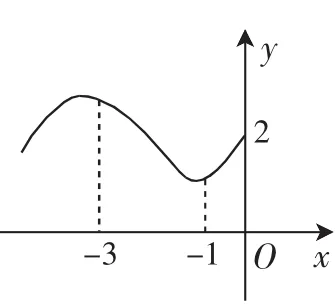
图4

设置目的：根据奇偶性的性质来逆向求解函数值，有效地开拓学生的视野，达到举一反三、触类旁通的目的.

四、变式训练探究

为了让学生从不同角度分析问题，深入认识并体会数学思想，教师应在日常教学中，采用一题多解、一题多变和一法多用三种变式进行变式训练.其中一题多解就是运用发散思维对同一道数学题采用不同的解题思路进行解题，有目的、有计划地将某个问题转化为其他问题，并不断总结和提炼不同的解决方法.例如，如图5所示，用5种颜色在图中4块空白位置染色，要求同一条边两侧颜色不同，试求共有多少种方案.

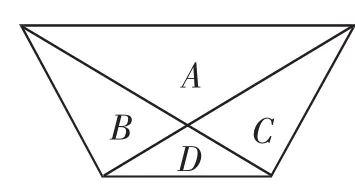
图5

解析：对于该题，可以采用分类的方法进行解题，即先按照颜色进行分类，再进行分步填充，也可以采用分步的方法进行解题，即先按A、D颜色相同或不同进行分类，再分步解决问题.但总的来说，全部都是应用计数原理来解决计数问题.

一题多变就是将题目中的已知条件交换，使一道题目变成一类题目，从而有效地培养学生的独创思维.

例如，已知△ABC两个顶点分别为点A（0，5），点B（0，-5），其余两边斜率的乘积为则求点C的轨迹方程.

在上述例题的基础上，笔者以例题中涉及的知识实质为依据，多角度且多层次地设置了如下变式题目.

变式1：已知两点的坐标分别为（0，-b）和（0，b），平面内一点C分别连接以上两点，且连接后所形成的相交直线的斜率之积为，求平面内点C所形成的轨迹方程.

变式2：若两点的坐标分别为（-a，0）和（a，0），其他条件同上，求点C所形成的轨迹方程.

变式3：已知M、N为双曲线上的两点，O为原点，P为MN的中点，求证：kMNkPO为定值.

一法多用就是解题的思路和方式是相同的，但题目本身可能相差很大，或者甚至一点联系都没有.

例如，如图6所示，在三棱锥S-ABC中，已知点D、E、F分别位于AC、BC、SC的中点，求证：平面DEF∥平面SAB.

在上述例题的基础上，笔者以证明面面平行的基本思路为依据，应用三角形的中位线和面面平行的判定定理设置了如下变式题目.

变式1：如图7所示，在正方体ABCD-A1B1C1D1中，O为底面ABCD的中心，P为DD1的中点，设Q是CC1上的点.试求当点Q位于什么位置时，才能使平面PAO∥平面D1BQ.

变式2：如图8所示，在正方体ABCD-A1B1C1D1中，E、F、G、S分别是BC、DC、SC、B1D1的中点，求证：平面BB1DD1∥平面EFG.

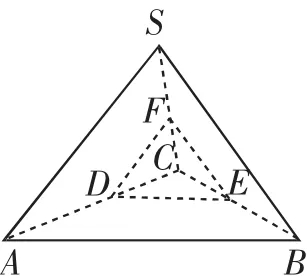
图6

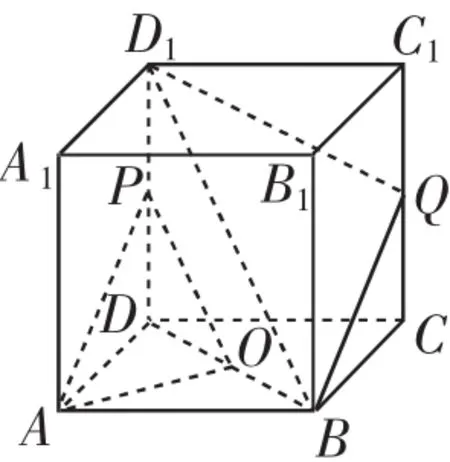
图7

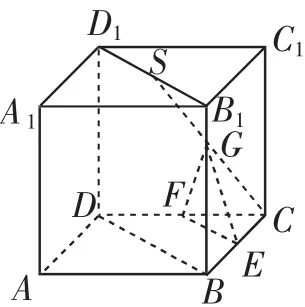
图8

总之，与传统的教学模式相比，基于变式引申的探究对广大教育者提出了更加严格的要求，也改变了“传输知识给学生”的局面，使得高中数学教学向着“自主、合作、研究”的方向发展，因此，在具体的教学实践中，教师应合理地设计变式训练，充分在课堂中引入，在辨析论证、巩固应用、总结提升等环节中不断鼓励学生积累知识，达到理解的最高维度——移情，从而提升和发展数学能力.