高中生数学学习能力差异的实践思考*

☉江苏省泰兴中学 李建新

刚刚升入高中的学生往往会觉得数学学习难度很大，很多学生在数学学习上总存在着上课能听懂但考试考不好的现象.初中数学知识的难度和容量相对来说都不大，因此，初中数学教师往往因为教学内容的难度低、容量小而采取重复讲解的方式，学生经过大量的重复练习之后往往会取得较为理想的成绩，但高中数学教学内容存在容量大、难度高的显著特点，学生在有限的学习时间内往往无法对知识的重难点形成较好的理解，“听得懂、做不对”的现象也会随之产生.笔者认为，让学生获得有意义的练习并能从练习中产生正确的领悟是至关重要的，因此，高中数学教师应着眼于“练”“悟”并进行有的放矢的教学，才能令学生获得“举一反三”的领悟.

一、“练”中锻炼数学能力

1.审题能力在“练”中的提升

每个数学问题的解决都离不开审题这一正确解题的基础，在了解、熟悉、掌握题意的基础上弄清已知和已知、已知和未知之间的关系并获得解题方法即为审题.有效的审题能够帮助学生顺利地理清题中各条件之间的关系并获得准确的解题方向.

2.语言表达能力在“练”中的提升

数学试题往往借助文字、图形和符号来表达，其中以文字的表达居多，将文字语言转化成图形语言并运用符号语言来表达是数学解题的第二个重要环节.有意义的练习能够使学生在语言表达与转换上获得更多的体会和经验，因此顺利、圆满地解决问题离不开这一关键环节.

3.思维能力在“练”中的提升

学生在有意义的练习中往往能够领悟到难题中条件的等价转化与深度挖掘的技巧并获得思维能力的提升.典型的、具备代表性的习题所蕴含的内容往往也特别值得学生反复思索、回味与拓展，学生在练习中的斟酌也是其思维提升的关键环节.

4.运算能力与解题速度在“练”中的提升

近几年的数学高考试题呈现出了运算量大且复杂的特点，考生若想快速准确地解题则必须要有较强的运算能力与解题速度作为支撑，因此，熟记课本结论并简化运算过程是首当其冲的，除此以外，学生还应该充分熟悉各类题型的求解方法并能运用数形结合的思想来简化求解过程.

二、“悟”中升华数学能力

根据同一个知识点的不同角度能够编写出不同的命题，因此，机械的题海战术是根本行不通的，教师应围绕典型题目进行各种变式并促进学生领悟其中的知识点与解题技巧.

1.综合题解题后的反思能使解题者对解题活动进行新的审视、探讨、分析和研究，有意义的反思能使解题者对题中所涉及的数学知识与方法产生更加全面而深刻的理解.因此，教师应善于引导学生在解题后进行回顾和反思，引导学生对自己的解题思路与所走的弯路进行回顾，使学生在日积月累的回顾和反思中获得更多的解题感悟和经验，并最终获得解题能力的快速提升.

2.对题目展开联想并进行横向类比能使学生对解题的思考更加全面.因此，教师应善于引导学生从提问的类型与方式、解题方法、数学思想方法、与之相关的题目等四个方面进行联想，使学生在针对性的训练中学会联想和类比的方法，并在此基础上能够更好地对题目形成准确的分析，这是解题突破的关键.

3.变式训练能令学生在不同角度与情形下对概念的本质加深理解，在突出问题结构特征的同时令概念的本质与外延得到凸显，使学生能够在揭示知识内在联系的同时获得发散思维的培养，最终达到以点带面的学习效果.因此，教师应善于进行变式设计并逐步引导学生在有意义的变式训练中学会变式的方法，掌握变式的真谛，并因此顺利构建起丰富而完整的知识脉络.

三、案例分析

例题已知x、y为正实数，若x+2y=1，求的最小值.

解：因为x、y为正实数，x+2y=1，

当且仅当时取等号.

变式1：已知实数x＞y＞0，且x+y=2，则的最小值是______.

解：由x+y=2，得2x+2y=4，即（x+3y）+（x-y）=4.于是有

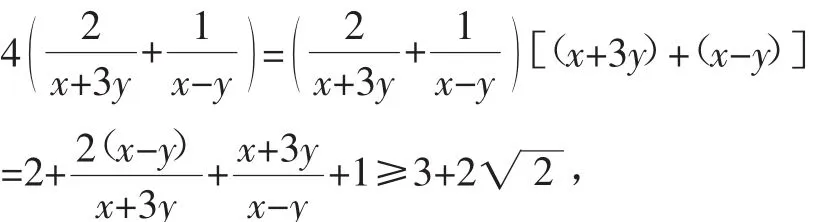
变式2：已知a＞0，b＞0，且，则a+2b的最小值是______.

解：令则

所以a+2b的最小值是

变式3：已知正实数x，y满足的最小值是______.

解：因为x＞0，y＞0，且

所以

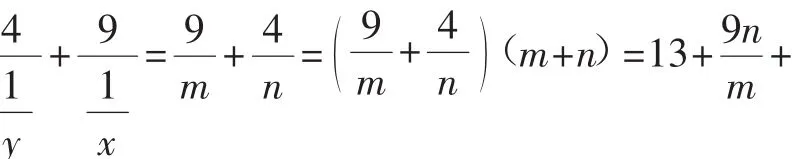
反思：上述例题的难度并不大，大多数学生能够较好地完成，但也有相当一部分的学生因为例题的变化而感觉难度颇大，平时所说的“听得懂、做不到”的现象也就难以避免了，因此，教师在实际教学中应注重学生“练”与“悟”的训练，精选例题与习题并为学生的有效练习创造平台，针对学生的练习进行有意义的引导并促进学生对数学知识、方法的吸收、领悟，以及对基本题目的演变过程、演变方法和演变技巧进行体会，并从根本上促进学生对数学知识和方法的融会贯通，使学生在有意义的“练”和“悟”的过程中获得“举一反三”的领悟.W