数列板块第二轮复习备考建议

广东省华南师范大学数学科学学院(510631) 林艳冬

数列是高中数学的核心内容之一,也是高考命题的热点之一,新课标把数列放在了选择性必修的部分,和以往注重对解题技巧的考查相比,新课标更注重体现数列是特殊的函数的观点.随着高考对数列题目的前移,对数列的考查要求较低,要强化通性通法的复习与训练,不要加大数列难题的训练.

一、全国新课标I卷近三年高考考点及分析

为了更好的分析和把握近三年来我国高考中数列这一重点知识模块的考点,笔者整理了下表;

表1：全国I卷文理科近三年数列的考点

考点分析

1.题型与分值全国新课标I卷对数列的考查,比较稳定.近三年理科卷基本上为两小题,分值10分,近三年文科卷为一大题,分值为12分.通过表一,我们不难发现数列是高考必考的内容,但近三年来难度有所以降低.理科卷的其中一题在前四题的位置,考察基本量的运算,难度较简单,另一题的考察较为灵活,难度中等.文科卷在第一道大题的位置,难度中等偏易.

2.主要考察的内容

近三年全国新课标I卷对数列主要考察的内容有：等差数列与等比数列,数列的通项公式,数列前n项和,数列的综合应用等.

3.文理科的差异

近三年全国新课标I卷数列文理科考察相同之处;都考察了数列的重点内容,都考察了等差和等比数列的概念、性质、通项公式、前n项和的内容,基本量的运算,求数列通项公式与求数列前n项和的方法.都考察了学生的运算求解能力、推理论证能力、抽象概括能力,转化与化归的思想.

近三年全国新课标I卷数列文理科考察不同之处;在题型上,理科是两道小题;文科是一道大题.在难度上,理科一道题在前四题的位置难度简单,另一道题难度中等,也可能会出现在选择题压轴题的位置,题目较为灵活;文科位于第一道大题的位置,难度中等,题目中规中矩.在内容上,理科考察内容综合创新,注重数列是特殊函数这一性质;文科考察偏向求数列通项公式与前n项和,证明等差、等比数列.在能力上,理科对运算求解能力、推理论证能力、创新探究能力都比文科要求要高.

二、高三二轮复习备考建议

基于以上分析的2016-2018年全国新课标I卷数列部分考察的内容与特点,建议备考时做到以下几点：

1.注重双基,降低难度.

掌握两类特殊的数列：等差数列和等比数列的概念、性质、通项公式、前n项和及其应用与计算,重视Sn与an的关系.

熟练掌握解决问题的方法和规律

全国新课标I卷对数列的考查要求较低,要强化通性通法的复习与训练,不要加大数列难题的训练.

2.突出数列是特殊函数的特点.

普通高中数学新课程标准(2017年版)把数列部分放在选择性必修的函数主题中,让学生感受数列与函数的共性与差异,因此在复习中要重视数列是特殊的函数这个概念的理解.

3.重视思想方法与能力的运用.

数列除了考查数列本身的基础知识外,还综合考查函数与方程思想、转化与化归思想、分类讨论的思想,运算求解能力、推理论证能力、抽象概括能力、创新探究能力等.因此,在复习数列时,既要突出基础性,还要对成绩中上学生(尤其是尖子生)强化思想方法的训练,要善于用函数的思想解决数列的问题.

4.关注易错点.

关注学生的易错点,有针对性的进行训练,数列部分常见的易错点有：

三、几种常见类型问题

为了使高考复习更加有针对性,笔者通过整理近3年全国I、II、III文理卷相同考点分布情况,总结出六种常考题型,希望能够给读者提供一定的启示.

题型一：基本量运用

表2：近三年全国卷数列基本量考察统计表

由表2可以发现全国卷对数列基本量几乎每年都要考察,而且很多题目都是渗透了基本量的运算,很多题目只考察简单定义与运算,难度较小,只要学生牢牢掌握住等差、等比数列基本量的关系即可解决问题,平时训练常用的通性通法即可.

例1 (2017年高考全国II卷文科第17题)已知等差数列{an}的前n项和为Sn,等比数列{bn}的前n项和为Tn,a1=-1,b1=1,a2+b2=2.

(1)若a3+b3=5,求{bn}的通项公式;

(2)若T3=21,求S3.

解析(1)设{an}的公差为d,{bn}的公比为q,则an=-1+(n-1)d,bn=qn-1.由a2+b2=2,得d+q=3.又由a3+b3=5,得2d+q2=6.联立和解得：因此{bn}的通项公式为bn=2n-1,n∈N∗.

(2)由b1=1,T3=21,得q2+q-20=0.解得q=-5,q=4.当q=-5时,由 ①得：d=8,则S3=21.当q=4时,由 ①得：d=-1,则S3=-6.

总结在解有关等差等比数列的问题时可以考虑化归为a1和d(q)等基本量,通过建立方程(组)获得解.共涉及五个量a1,d(q),n,an,Sn,知其中三个就能求另外两个,即知三求二,体现了用方程的思想解决问题和运算求解能力,分类讨论的思想.

题型二：数列性质

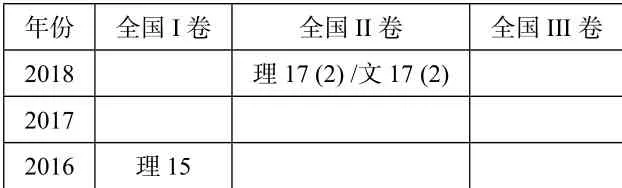
表3：近三年全国卷数列的性质考察统计表

新课标更注重数列是一类特殊函数这一性质,故数列可以运用很多函数的性质解决问题,特别是求最值的问题(如2017年全国II卷理科第17题;2017年全国II卷文科第17题).

例2 (2016年高考全国I卷理科第15题)设等比数列{an}满足a1+a3=10,a2+a4=5,则a1a2···an的最大值为____.

解析因为数列{an}是等比数列,所以可设an=a1qn-1,其中a1为首项,q为公比,根据题干条件有所以an=即数列{an}是递减数列,且当n≤4时,an≥1;当n≥5时,0＜an＜1;所以当n=3或4时,a1a2···an最大,且最大值Tn为64.故本题正确答案为64.

总结了解数列是自变量为正整数的一类函数,了解等差数列与一次函数的关系,等比数列与指数函数的关系,等差数列前n项和与二次函数的关系,利用函数的单调性求最值是高考中常见的题型,但要注意函数单调性与数列单调性的区别.渗透函数与方程的思想、转化与化归思想.

题型三：判断与证明等差数列或等比数列

表4：近三年全国卷判断与证明等差、等比数列考察统计表

判断与证明等差数列或等比数列是高考中的一个基本题型,常出现在17题的位置,与求数列的通项公式一起考察,备考要求学生牢固掌握等差数列与等比数列的定义,掌握判断与证明等差数列或等比数列的方法.

(1)判断与证明等差数列的方法

(2)判断与证明等比数列的方法

例3(2017年高考全国卷I文科第17题)记Sn为等比数列{an}的前n项和,已知S2=2,S3=-6,

(1)求{an}的通项公式.

(2)求Sn,并判断Sn+1,Sn,Sn+2是否为等差数列.

解析(1)设{an}的公比为q. 由题意可得解得q=-2,a1=-2.故{an}的通项公式为an=(-2)n.

总结需多加强判断与证明等差数列或等比数列的通性通法的训练,判断与证明等差数列或等比数列也常与求数列通项公式一起考察.

题型四：求通项公式

表5：近三年全国卷数列求通项公式考察统计表

由表五可以看出,全国卷在求数列通项公式的考察频率上特别高,特别是文科试卷近三年都有考察,在备考时要求学生掌握常见的求通项公式的方法,多加强通性通法的训练.常见的求数列的通项公式的方法有：

例4(2018年高考全国卷I文科第17题)已知数列{an}满足a1=1,nan+1=2(n+1)an,设

(1)求b1,b2,b3;

(2)判断数列{bn}是否为等比数列,并说明理由;

(3)求{an}的通项公式.

解法1

(2){bn}是首项为1,公比为2的等比数列.由条件可得即bn+1=2bn,又b1=1,所以{bn}是首项为1,公比为2的等比数列.

解法2 (先做第二问,第三问用数学归纳法)

(1)由nan+1=2(n+1)an可得即bn+1=2bn,又b1=1,所以{bn}是首项为1,公比为2的等比数列,所以bn=2n-1.从而,b1=1,b2=2,b3=4.

(2)由(1)可知所以{bn}是首项为1,公比为2的等比数列.

(3)猜想an=n·2n-1.以下用数学归纳法给予证明.

1)当n=1时,a1=1×20=1,猜想成立.

2)假设当n=k时,ak=k·2k-1成立的,则当n=k+1时,由nan+1=2(n+1)an,可得所以当n=k+1时,an=n·2n-1成立.

解法3(用累乘法先求第三问)

(3)由nan+1=2(n+1)an可得当n≥2时,当n=1时,a1=1×20=1,满足上式.所以an=n·2n-1.

(1)由(2)可知,b1=1,b2=2,b3=4.

总结本题难度不大,但解题的思路很多,可以按照题目的顺序,先证明构造好的数列是等差数列,再求通项公式,也可以通过猜想公式再用数学归纳法证明,还可以直接通过累乘法求通项公式.可见现在的数列题更多的是考察学生综合的运用能力,应该更多的注重基本知识基本能力的训练.

例5(2018年高考全国I卷理科第14题)记Sn为数列{an}的前n项和.若Sn=2an+1,则S6=____.

解析因为Sn=2an+1,所以a1=2a1+1,a1=-1,又因为Sn+1-Sn=2an+1-2an=an+1,所以an+1=2an,又因为a1+a2=2a2+1,所以a2=-2,故{an}是以-1为首项,2为公比的等比数列,所以an=(-1)2n-1,故当n=6时,S6=1-26=-63,故本题正确答案为-63.

总结利用Sn与an的关系求通项公式,是求通项公式的核心方法,也是高考常考的题型,需多加强这一题型的训练,在解题时要注意n=1的情况,渗透分类讨论的思想.

题型五：求数列的前n项和

表：近三年全国卷求数列的前n项和考察统计表

由表6可以看出数列的前n项和是高考常见的考点,数列的前n项和是数列的重要特征量,在备考时要求学生掌握常见的求通项公式的方法,需要多加强通性通法的训练,常见的求数列的通项公式的方法有：

常见的裂项方法：

③错位相减法：如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的,若an=bn·cn,其中{bn}是等差数列,{cn}是公比为q的等比数列(如2014年全国I卷文科第17题).

例6(2017年全国III卷文科第17题)设数列{an}满足a1+3a2+···+(2n-1)an=2n.

(1)求{an}的通项公式;

解析(1)因为,a1+3a2+···+(2n-1)an=2n①,所以n≥2时,a1+3a2+···+(2n-3)an-1=2(n-1)②, ①-②得,(2n-1)an=2,又n=1时,a1=2适合上式.所以

总结本题难度不大,第1小题运用了利用Sn与an的关系求通项公式,注意当n=1时的情况.第2题运用了裂项相消法求数列前n项和,掌握常见的相消的方法即可解决.本题渗透了化归与转化,分类讨论的思想.

题型六.创新题型

表7：近三年全国卷数列创新题型考察统计表

数列在实际生活中也有着广泛的应用,随着高考对创新意识和能力要求的进一步增加,这一部分内容也将受到越来越多的关注.数列创新题也应随之受到重视.

例7 (2017年高考全国I卷理科第12题)几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案：已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N：N＞100且该数列的前N项和为2的整数幂.那么该款软件的激活码是( )

A.440 B.330 C.220 D.110

解析当N=110时,所以S110=(21-1)+(22-1)+(23-1)+···+(214-1)+1+2+22+23+24=-14+31=215+15不为2的整数幂,排除D;当N=220时,所以S220=(21-1)+(22-1)+(23-1)+···+(220-1)+1+2+22+···+29==221+210-23不为2的整数幂,排除C;当N=330时,330=所以S330=(21-1)+(22-1)+(23-1)+···+(225-1)+1+2+22+23+24=-25+31=226+4不为2的整数幂,排除B;当N=440时,所以S440=(21-1)+(22-1)+(23-1)+···+(229-1)+1+2+22+23+24=-29+31=230,故选A.

总结数列创新题通过创设新颖情境,要求考生灵活运用所学数学知识,分析问题并解决问题,同时为考查考生创新应用意识创设了平台,对考生的阅读理解能力、推理论证能力及理性思维进行了全面的考查.

虽然数列部分近三年来考察较为简单,但仍然是高考一个重要的考点,也综合考查函数与方程思想、转化与化归思想、分类讨论的思想,运算求解能力、推理论证能力、抽象概括能力、创新探究能力等.在备考时仍然需要引起重视,建议强化数列部分通性通法的复习与训练,不要加大数列难题与技巧类题目的训练.