推理与证明综合演练卷答案与提示

一、选择题

1.B

2.A 三段论中的大前提，小前提以及推理形式都是正确的，所以结论正确。

3.B

4.B 利用类比思想结合向量的定义及性质，特别是向量的数量积的定义可知①正确，②③④不正确。

5.C因此，此数列具有周期性依次重复出现，所以

6.C 正三角形的边对应正四面体的面，也即正三角形所在的正四面体的侧面，所以边的中点对应的就是正四面体中各正三角形的中心。故选C。

7.A 分别令n=1，2，3，所以

8.C

9.D 用反证法证题时一定要将对立面找全。在①中应假设p+q＞2，故①的假设是错误的。而②的假设是正确的，故选D。

10.Af(x)=x3+x是奇函数，且在R上是增函数。由a+b＞0，得a＞-b。

所以f(a)＞f(-b)，即f(a)+f(b)＞0。同理f(a)+f(c)＞0，f(b)+f(c)＞0，所以f(a)+f(b)+f(c)＞0。

11.B

12.A 假设＞0，则1+y≥2x，1+x≥2y⇒2+x+y≥2x+2y⇒x+y≤2，这与条件矛盾。

13.A 从各个等式可以看出，等式右端均为2，左端为两个分式的和，且两个式子的分子之和等于8，分母则为相应分子减去4，设其中一个分子为n，另一个分子必为8-n。

14.C 由题意设O为正四面体的外接球、内切球球心，设正四面体的高为h，由等体积法可求得内切球半径为，外接球半径为，所以

15.B 由于k是偶数，故k+2是k后面的第一个偶数。

16.C 要使恒成立，只需而所以n≤4，即n的最大值为4。

二、填空题

17.在四面体A-B C D中，G为△B C D的重心，则

18.对于任意x1，x2∈R 且x1＜x2，有f(x1)＞f(x2)

19.1提示：只有③不正确。

20.提示：n≥2，故第一步应证明当n=2时不等式成立，即

21.nn

三、解答题

22.假设

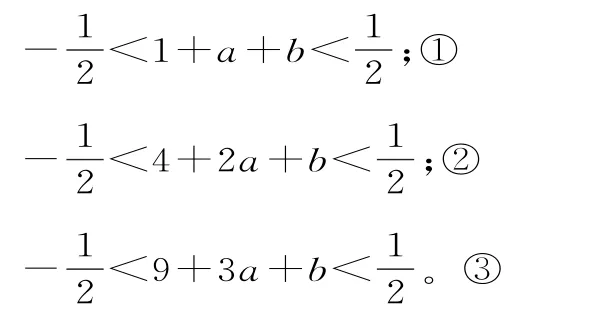
于是：①+③，得-1＜10+4a+2b＜1。

当n=k+1时，则：，这与②矛盾。

所以假设不成立，即|f(1)|，|f(2)|，|f(3)|中至少有一个不小于

23.易知

24.(1)由表知，每行的第一个数为偶数，所以第n+1行的第一个数为2n，所以第n行的最后一个数为2n-1。

(2)由(1)知第n-1行的最后一个数为2n-1-1，第n行的第一个数为2n-1，第n行的最后一个数为2n-1。又由观察知，每行数字的个数与这一行的第一个数相同，所以由等差数列求和公式得Sn=2(2n-3)+2(2n-2)-2(n-2)。

(3)因为210=1024，211=2048，又第11行最后一个数为211-1=2047，所以2008是在第11行中，由等差数列的通项公式得，2008是第11行的第985个数。

25.(1)当n=1时，因为所以原不等式成立。

(2)假设n=k时，原不等式成立，即有

因此，欲证当n=k+1时原不等式成立，只需证明成立，即证

于是当n=k+1时，原不等式也成立。

由(1)(2)可知，当n是一切正整数时，原不等式都成立。

26.(1)c1，c2，c3，c4分别是9，11，12，13。

(2)数列｛cn｝由｛an｝，｛bn｝的项构成，只需讨论数列｛an｝的项是否为数列｛bn｝的项。

因为a2n-1=3(2n-1)+6=6n+3=2(3n-2)+7=b3n-2，所以a2n-1是｛bn｝的项。

下面用反证法证明：a2n不是｛bn｝的项。

假设a2n是数列｛bn｝的项，设a2n=bm，则与m为正整数矛盾。

结论得证。