浅谈复数中常见的错题剖析

■河南省罗山高级中学 王 莉

在解复数试题时，不少同学经常做错。有些问题往往是由于大家对概念的模糊认识，从而造成一些看起来正确实际上错误的做法，致使我们的解题思路偏离实际。

误区一：对纯虚数的概念把握不准导致错误

例1设m∈R，m2+m-2+(m2-1)i是纯虚数，其中i是虚数单位，则m=_________。

错解：因为m∈R，复数m2+m-2+(m2-1)i是纯虚数，所以m2+m-2=0。解得m=1或m=-2。

正解：m∈R，复数m2+m-2+(m2-1)i是纯虚数的充要条件是：

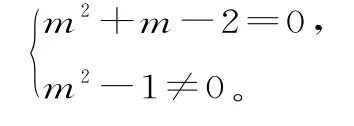
也即m=-2。

故m=-2时，m2+m-2+(m2-1)i是纯虚数。

剖析：(1)若忽视“纯虚数的虚部不为0”这一条件，易得出m=1或m=-2的错误结论。

(2)复数z=a+bi(a，b∈R)是纯虚数的充要条件为二者缺一不可。

误区二：对复数的几何意义理解不深，从而导致错误

例2(2016年高考新课标Ⅱ卷理数)已知z=(m+3)+(m-1)i在复平面内对应的点在第四象限，则实数m的取值范围是( )。

A.(-3，1) B.(-1，3)

C.[-1，3] D.(-∞，-3)

错解：要使复数对应的点在第四象限应满足无解。

正解：要使复数对应的点在第四象限，应满足：解得-3＜m＜1，故选A。

剖析：没有理解复数的几何意义，不知道如何将复数与复平面内的点对应。

误区三：对复数的运算不熟悉导致错误

例3(2016年高考新课标Ⅲ卷理数)若z=1+2 i，则

A.1 B.-1 C.i D.-i

错解：选D。

正解：故选C。

剖析：把实数的运算与复数运算混淆。

误区四：误用判别式求解复数方程

例4已知关于x的方程x2+(k+2 i)x+2+ki=0有实数根，求实数k应满足的条件。

错解：由于方程有实数根，得Δ=(k+2 i)2-4(2+ki)≥0，解得或k≤

正解：设x=x0是方程的实数根，代入方程并整理得(x20+k x0+2)+(2x0+k)i=0。由复数相等的充要条件，得解得或

剖析：(1)求解本题容易出现如下错误：因为方程有实根，所以Δ=(k+2 i)2-4(2+ki)≥0，解得或需注意由于虚数单位的特殊性，不能用判别式判断复系数一元二次方程有无实数根。

(2)复数范围内解方程的一般思路是：依题意设出方程的根，代入方程，利用复数相等的充要条件求解。对于一元二次方程，也可以用求根公式求解，要注意在复数范围内负数能开方的，此外，根与系数的关系也是成立的，注意求方程中参数的取值时，不能利用判别式求解。

误区五：复数的“模”与“绝对值”混淆出错

例5在复数范围内解不等式|z2-4z+3|＜|z-1|。

错解：原不等式⇔|z-3||z-1|＜|z-1|⇔|z-1|(|z-3|-1)＜0。

因为|z-1|≥0，所以|z-3|＜1。

解得-1＜z-3＜1，即2＜z＜4。

正解：原不等式⇔|z-3||z-1|＜|z-1|⇔|z-1|(|z-3|-1)＜0。

因为|z-1|≥0，所以|z-3|＜1，且z≠1。

其解为以点(3，0)为圆心，1为半径的圆内部。

剖析：错在把实数中绝对值的性质“|x|＜a⇔-a＜x＜a(a＞0)”生搬硬套到复数模中来。

总而言之，在做复数这部分的习题时出现的五花八门的错误，其根源在于基础理论知识掌握不牢靠，请同学们在平时多多留心，认真对待每一道题，让细心成为我们生活的常态，希望本文对同学们掌握复数这类题型有所帮助。