函数与导数综合演练（A卷）答案与提示

一、选择题

1.【答案】D

提示：由于f(x)为奇函数，所以f(-x)=-f(x)，解得a=1。因此，f(x)=x3+x，解得f'(0)=1，故曲线y=f(x)在点(0，0)处的切线方程为y=x，选D。

2.【答案】A

提示：当x＜1时，f'(x)＜0，函数递减；当x＞1时，f'(x)＞0，函数递增。当x=1时，函数取得极小值同时也是最小值f(1)，所以f(0)＞f(1)，f(2)＞f(1)，故f(0)+f(2)＞2f(1)，选A。

3.【答案】B

提示：函数的导数为f'(x)=3x2+2a x+(a-3)。若f'(x)为偶函数，则a=0，f(x)=x3-3x，f'(x)=3x2-3。所以f'(0)=-3。因此，在原点处的切线方程为y=-3x，选B。

4.【答案】D

提示：根据定积分的应用可知，所求面积为，选D。

5.【答案】A

提示：所以在点(4，e2)处的导数为，即切线斜率k=故切线方程为令x=0，得y=-e2。令y=0，得x=2。所围三角形的面积为，选A。

6.【答案】A

提示：所以曲线在点P(-1，0)处的切线斜率，切线方程为y=x-(-1)=x+1，选A。

7.【答案】B

提示：由定积分的应用知，所求面积为：

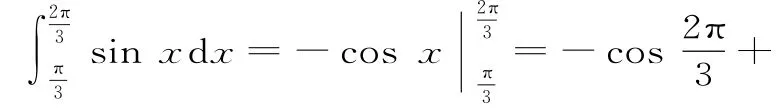
8.【答案】C

提示：函数过原点，所以d=0。由图像知f(-1)=0且f(2)=0，即-1+b-c=0且8+4b+2c=0，解得b=-1，c=-2，所以函数f(x)=x3-x2-2x。因此，f'(x)=3x2-2x-2。由题意知x1，x2是导函数的极值点，所以x1，x2是f'(x)=0的两个根，所以+=

9.【答案】B

提示：即切线在x=0处的斜率为-l n2。所以切线方程为y-1=-l n2(x-0)，即xl n2+y-1=0，选B。

10.【答案】D

提示：，故选D。

11.【答案】D

提示：由得(x2-，解得t=4或t=-2(舍去)，选D。

12.【答案】C

提示：f'(x)=2a x+b，f'(0)=b＞0，函数f(x)的值域为[0，+∞)，所以a＞0，且，即4a c=b2，c＞0。因此，f(1)所以最小值为2，选C。

13.【答案】C

提示：令函数F(x)=x f(x)，则函数F(x)=x f(x)为偶函数。当x＞0时，F'(x)=f(x)+x f'(x)＞0，此时函数递增。

14.【答案】C

提示：由题意知，则

15.【答案】D

提示：函数的导数为f'(x)=12x2-2a x-2b，导函数在x=1处有极值，则f'(1)=12-2a-2b=0，即a+b=6。

16.【答案】D

提示：因为，所以f'(x)因此，选D。

17.【答案】B

提示：设F(x)=f(x)-(2x+4)，则F(-1)=f(-1)-(-2+4)=2-2=0。

F'(x)=f'(x)-2，则对任意x∈R，F'(x)=f'(x)-2＞0，即函数F(x)在R上单调递增。故F(x)＞0的解集为(-1，+∞)，即f(x)＞2x+4的解集为(-1，+∞)，选B。

18.【答案】B

提示：因为函数y=e(a-1)x+4x，所以y'=(a-1)e(a-1)x+4(a＜1)，导函数的零点为因为函数y=e(a-1)x+4x(x∈R)有大于零的极值点，所以

提示：，故两条曲线在点P(1，1)的斜率分别为，解得a＜-3，选B。

19.【答案】Ak2=a。因为l1⊥l2，所以=-2，选A。

20.【答案】A

提示：利用基本不等式可得f(x)的最小值为2 e，对函数g(x)求导，利用导数研究函数g(x)的单调性，进而可求得g(x)的最大值为e。得到关于k的不等式，解得k≥1。选A。

21.【答案】D

提示：在(0，3)上递减，在[3，+∞)上递增。，根据零点存在定理可知，选D。

22.【答案】D

提示：函数的导数为f'(x)=3x2-a，要使函数在[1，+∞)上是单调增函数，则有f'(x)=3x2-a≥0恒成立，即a≤3x2。又3x2≥3，故a≤3，即a的最大值是3，选D。

二、填空题

23.【答案】

提示：

24.【答案】

提示：函数y=x2的导数为y'=2x，即在A处的切线斜率为k=2，所以切线方程为y-1=2(x-1)，即y=2x-1。由y=2x-1，y=x2，解得x=1。所以所求面积为

2

5.【答案】a≥

提示：f'(x)=ex+xex=(1+x)ex，当x＞-1时，f'(x)＞0，函数递增；当x＜-1时，f'(x)＜0，函数递减。所以当x=-1时f(x)取得极小值，即最小值f(-1)=-函数g(x)的最大值为a，若∃x1，x2∈R使得f(x2)≤g(x1)成立，则g(x)的最大值大于或等于f(x)的最小值，即

26.【答案】

提示：由得x=1或x=-3。所以曲线y=3-x2和直线y=2x所围成封闭图形的面积为

27.【答案】x+y+1=0

提示：函数的导数为f'(x)=2f'(1)+令x=1，则f'(1)=2f'(1)+1，解得f'(1)=-1，即f(x)=2x f'(1)+l nx=-2x+l nx，所以f(1)=-2+l n1=-2。因此，在点M(1，-2)处的切线方程为y-(-2)=-(x-1)，即x+y+1=0。

28.【答案】1

提示：8+2t=10，解得t=1。

29.【答案】m＞n

提示：，则m＞n。

30.【答案】

提示：根据定积分的几何意义可知等于半径为1的半圆的面积，即=0，所以

31.【答案】-

32.【答案】(-2，2)

提示：由f(x)=x3-3x+a，得f'(x)=3x2-3。当f'(x)=3x2-3=0，得x=±1。由图像可知f(x)极大值=f(-1)=2+a，f(x)极小值=f(1)=a-2，要使函数f(x)=x3-3x+a有三个不同的零点，则有f(x)极大值=2+a＞0，f(x)极小值=a-2＜0，即-2＜a＜2。所以实数a的取值范围是(-2，2)。

33.【答案】①②④

提示：由导数图像可知，当-1＜x＜0或2＜x＜4时，f'(x)＞0，函数单调递增；当0＜x＜2或4＜x＜5时，f'(x)＜0，函数单调递减；当x=0和x=4时，函数取得极大值f(0)=2，f(4)=2；当x=2时，函数取得极小值f(2)。又f(-1)=f(5)=1，所以函数的最大值为2，最小值为1，值域为[1，2]，①正确。②正确。因为在当x=0和x=4时，函数取得极大值f(0)=2，f(4)=2，要使当x∈[-1，t]时，函数f(x)的最大值是2，且2≤t≤5，所以t的最大值为5，③不正确。由f(x)=a知，因为极小值f(2)=1.5，极大值为f(0)=f(4)=2，所以当1＜a＜2时，y=f(x)-a最多有4个零点，所以④正确。

因此，真命题的序号为①②④。

三、解答题

34.

(1)对一切x∈(0，+∞)，f(x)≥g(x)恒成立，即xl nx-a x≥-x2-2。故a≤l n在x∈(0，+∞)上恒成立。

当x∈(0，1)时F'(x)＜0；当x∈(1，+∞)时，F'(x)＞0。因此，F(x)在x=1处取极小值，也是最小值，即F(x)min=F(1)=3。

所以a≤3。

(2)当a=-1 时，f(x)=xl nx+x，f'(x)=l nx+2。由f'(x)=0，得

因此，f(x)在处取得极小值，也是最小值

由于f(m)＜0，f(m+3)=(m+3)·[l n

(m+3)+1]＞0，因此，f(x)max=f(m+3)=(m+3)[l n(m+3)+1]。

由(2)知a=-1时，f(x)=xl nx+x的最小值是当且仅当时取得。设则G'(x)易知当x=1时，G(x)取得最大值，又从而可知对一切x∈(0，+∞)，都有成立。

35.

(1)由题意知，直线y=x+2的斜率为1，函数f(x)的定义域为(0，+∞)。因为，所以-1。解得a=1，故

由f'(x)＞0，解得x＞2；

由f'(x)＜0，解得0＜x＜2。

所以f(x)的单调增区间是(2，+∞)，单调减区间是(0，2)。

由f'(x)＞0，解得

由f'(x)＜0，解得

所以f(x)在区间上单调递增，在区间上单调递减。当时，函数f(x)取得最小值因为对于∀x∈(0，+∞)都有f(x)＞2(a-1)成立，所以即可。

(3)依题得所以a的取值范围是则由g'(x)＞0，解得x＞1；由g'(x)＜0，解得0＜x＜1。所以函数g(x)在区间(0，1)为减函数，在区间(1，+∞)为增函数。又因为函数g(x)在区间[e-1，e]上有两个零点，所以解得所以b的取值范围是

36.

(1)f(x)的定义域为(0，+∞)。当a=0时，f(x)=l nx+因为0，所以f(x)在[1，e]上是增函数。当x=1时，f(x)取得最小值f(1)=1。所以f(x)在[1，e]上的最小值为1。

抛物线g(x)=2x2-2a x+1开口向上，只需g(2)＞0或即可。

由g(2)＞0，即8-4a+1＞0，得

又因为x＞0，所以

设所以2a小于函数g(x)在区间上的最大值。

所以函数g(x)在区间上递增，在区间上递减，函数g(x)在或x=2处取得最大值。

令h(x)=2x2-2a x+1。

①显然，当a≤0时，在(0，+∞)上h(x)＞0恒成立，f'(x)＞0，此时函数f(x)没有极值点。

②当a＞0时：

(i)当Δ≤0，即0＜a≤时，易知，当时，在(0，+∞)上h(x)≥0恒成立，这时f'(x)≥0，此时，函数f(x)没有极值点；

(i i)当Δ＞0时，即时，h(x)＜0，f'(x)＜0；