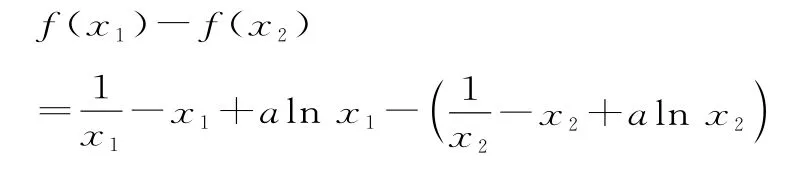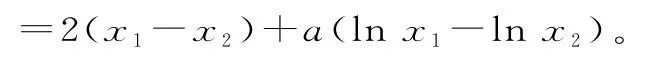函数与导数综合演练（B卷）答案与提示

一、选择题

1.【答案】B

提示：求出导函数由于函数f(x)=k x-l nx在区间(2，+∞)上单调递增，因此在区间(2，+∞)上恒成立，解得选B。

2.【答案】A

提示：函数f(x)=ex-l n(x+a)(a∈R)，则

3.【答案】A

提示：设则g'(x)=函数g(x)是R上的减函数。因为函数f(x+3)是偶函数，所以f(-x+3)=f(x+3)，函数关于x=3对称，f(0)=f(6)=1。不等式f(x)＞ex等价于g(x)＞1，即g(x)＞g(0)，x＜0。不等式f(x)＞ex的解集为(-∞，0)。选A。

4.【答案】C

提示：y'=3x2+2x-1=(3x-1)(x+1)。令y'＞0，解得或x＜-1。再令y'＜0，解得所以x=-1，x=分别是函数的极大值点和极小值点。因为-1，所以f(x)在[-2，1]上的最小值为-1，选C。

5.【答案】A

提示：由，可知，解得选A。

6.【答案】C

提示：函数在x=1处有极值，说明函数在x=1处的导数为0。因为f'(x)=3x2+2a x+b，所以f'(1)=3+2a+b=0。又因为f(1)=1+a+b+a2=10，所以联立上式可求得a=4，b=-11或a=-3，b=3。当a=-3，b=3时，f'(x)=3(x-1)2≥0在x=1处无极值，所以解析式为f(x)=x3+4x2-11x+16。f(2)=18，选C。

7.【答案】B

提示：构造函数求出导数由于∀x∈R，总有(2-x)f(x)+x f'(x)＜0，所以当x＞0时，g'(x)＜0，函数g(x)递减；当x＜0时，g'(x)＞0，函数g(x)递增。因此，g(x)＜g(0)=0，即恒成立，所以f(x)＜0恒成立，选B。

8.【答案】D

提示：函数的导数y'=恒有解，则a≠0，Δ=4a2+4a≥0，解得a≤-1或a＞0。检验知：当a=-1时无极值点，所以a＜-1或a＞0，选D。

9.【答案】D

提示：由于函数f(x)=x3-2x2+a x+3在[1，2]上单调递增，所以f'(x)=3x2-所以f(x)＜ex等价于4x+a≥0在[1，2]上恒成立。二次函数的对称轴为则f'(x)在[1，2]上单调递增，f'(x)min=f'(1)=-1+a≥0，解得a≥1，选D。

10.【答案】D

提示：由3x+a(2y-4 ex)(l ny-l nx)=0，得令则t＞0，3+2a(t-2 e)l nt=0，即(t-2 e)l nt有解。设g(t)=(t-2 e)l nt，则为增函数。因为g'(e)=，所以当t＞e时，g'(t)＞0；当0＜t＜e时，g'(t)＜0。即当t=e时，函数g(t)取得极小值g(e)=-e。即g(t)≥g(e)=-e。若(t-2 e)l n有解，则即a＜0或选D。

11.【答案】D

提示：0)。令f'(x)＞0，解得x＞2；令f'(x)＜0，解得0＜x＜2。f(x)在(0，2)上递减，在(2，+∞)上递增，x=2是函数的极小值点，选D。

12.【答案】A

提示：令其导数g'(x)=由∀x∈R都有f'(x)＞f(x)，则有g'(x)＞0，即函数g(x)在R上为增函数。又f(1)=e，则即g(x)＜g(1)，x＜1。因此，不等式f(x)＜ex的解集为(-∞，1)，选 A。

13.【答案】B

提示：令f(x)-a x2+1，则f'(x)=x2-2a x。因为a＞2，所以当x∈(0，2)时，f'(x)＜0，即f(x)在(0，2)上为减函数。又故函数在(0，2)上有且只有一零点，即方程在(0，2)上恰好有1个根，选B。

14.【答案】D

提示：根据导数函数图像可判断f(x)在(0，1)上单调递增，在(1，+∞)上单调递减。由△A B C为锐角三角形，得所以s i nA＜1，即0＜c o sB＜s i nA＜1，f(s i nA)＞f(c o sB)，选D。

15.【答案】D

提示：因为函数f(x)=ex(s i nxc o s

x)，所以f'(x)=2 exs i nx。令f'(x)=0，可得x=kπ(k∈z)。当x∈(2kπ，2kπ+π)时，f'(x)＞0，函数单调递增；当x∈(2kπ+π，2kπ+2 π)时，f'(x)＜0，函数单调递减。故当x=2kπ+π时，函数f(x)取得极大值，此时f(2kπ+π)=e2kπ+π[s i n(2kπ+π)-c o s(2kπ+π)]=e2kπ+π。又0≤x≤2019 π，所以函数f(x)的各极大值之和为eπ+e3π+e5π选D。

16.【答案】C

提示：由g(x)=g'(1)ex-1-g(0)x+得g'(x)=g'(1)ex-1-g(0)+x。则g'(1)=g'(1)-g(0)+1，解得g(0)=1。

又g(0)=g'(1)e-1，解得g'(1)=e。

17.【答案】A

提示：问题转化为对x∈(0，+∞)恒成立。令则令g'(x)＞0，解得x＞e2；令g'(x)＜0，解得0＜x＜e2。故g(x)在(0，e2)上递减，在(e2，+∞)上递增，g(x)的最小值是故k≤1-选A。

18.D

19.C

二、填空题

20.【答案】e

提示：由函数的解析式可得f'(x)=则f'(1)=e，即f'(1)的值为e。

21.【答案】-3

提示：y'=ex(a x+a+1)，则f'(0)=a+1=-2，所以a=-3。

22.【答案】-3

提示：由f'(x)=6x2-2a x=0，得x=0或因为函数f(x)在(0，+∞)上有且仅有一个零点，且f(0)=1，所以因此解得a=3。从而函数f(x)=2x3-3x2+1在[-1，0]上单调递增，在[0，1]上单调递减，所以f(x)max=f(0)=1。又f(-1)=-4，f(1)=0，所以f(x)min=-4，f(x)max+f(x)min=-3。

三、解答题

23.(1)因为f(x)=[a x2-(4a+1)x+4a+3]ex，所以f'(x)=[a x2-(2a+1)x+2]ex，f'(1)=(1-a)e。由题设知f'(1)=0，则(1-a)e=0，解得a=1。此时f(1)=3 e≠0，所以a的值为1。

(2)由(1)得f'(x)=[a x2-(2a+1)x+2]ex=(a x-1)(x-2)ex。

综上可知，a的取值范围是

24.(1)由得f'(x)则f'(0)=2，也即曲线y=f(x)在点(0，-1)处的切线斜率为2，所求切线方程为y=2x-1。

因为a≥1，所以

令f'(x)=0，则或x=2。

所以函数f(x)在和(2，+∞)上单调递减，在上单调递增。

①当x≥2时，a x2+x-1＞0，ex＞0，所以f(x)＞0，f(x)+e≥0。

②当x＜2时，f(x)在上单调递减，在上单调递增。

因为a≥1，所以可知

因此，当x＜2时

综上可知，当a≥1时，f(x)+e≥0。

25.(1)①由当-2≤a≤2时，Δ≤0，f'(x)≤0，此时f(x)在(0，+∞)上为单调递减。

②当Δ＞0时，a＜-2或a＞2，此时方程x2-a x+1=0两根为当a＜-2时，此时两根均为负，所以f'(x)在(0，+∞)上单调递减。当a＞2 时，Δ＞0，此 时f(x)在上 单 调 递 减，f(x)在上单调递增，f(x)在上单调递减。

综上可得，a≤2时，f(x)在(0，+∞)上单调递减；a＞2时，f(x)在上单调递减，f(x)在上单调递增。

(2)由(1)可得，x2-a x+1=0两根x1，x2则a＞2，且x1+x2=a，x1x2=1。令0＜x1＜x2，则