高考中推理与证明的创新题探索

■河南省罗山高级中学 王 盟

当下社会对科技创新尤为看重，创新需要人才，这就决定了高校要选拔具有创新潜质的人才，因而，高考数学必须重视对同学们创新意识的考查。推理与证明作为高中数学的选修部分，在近年来高考试题中都会有所体现，题目新颖，具有一定的创新性，所以同学们务必认真研究创新题的特点，仔细揣摩命题专家的设计意图，深刻领会“能力立意”的命题指导思想，准确解读《考试大纲》的要求，有益于大家的高效学习。鉴于此，下面拟对高考数学中有关推理与证明的创新题加以分析探究。

一、考纲解读

(一)合情推理与演绎推理

(1)了解合情推理的含义，能利用归纳和类比进行简单的推理，了解合情推理在数学发现中的作用；

(2)了解演绎推理的重要性，掌握演绎推理的基本模式，并能运用演绎推理进行一些简单的推理；

(3)了解合情推理和演绎推理之间的联系和差异。

(二)直接证明与间接证明

(1)了解直接证明的两种基本方法——分析法和综合法，了解分析法和综合法的思考过程、特点；

(2)了解间接证明的一种基本方法——反证法，了解反证法的思考过程、特点。

(三)数学归纳法

了解数学归纳法的原理，能用数学归纳法证明一些简单的数学命题。

二、核心考点突破

考向1：合情推理

考情聚焦：①合情推理能够考查同学们观察、分析、比较、联想的能力，在高考中越来越受到重视；②多与其他知识综合，属中档题。

考向链接：①归纳推理是由部分到整体，由个别到一般的推理，在进行归纳时，要先根据已知的部分个体，把它们适当变形，找出它们之间的联系，从而归纳出一般结论；②类比推理是由特殊到特殊的推理，是两个类似对象之间的推理，其中一个对象具有某个性质，推理另一个对象也具有类似的性质。在进行类比时，要充分考虑已知对象的性质，然后类比推导另一个对象的性质。

例1(2016年山东卷)观察下列等式：

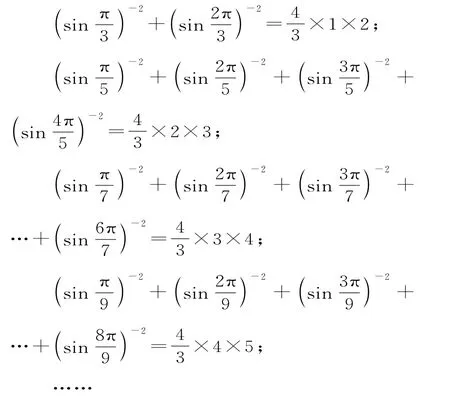
【命题立意】本题主要考查同学们利用合情推理的方法对式子进行归纳求解的能力。

【思路点拨】利用归纳推理求解。

解析：通过类比，可以发现，最前面的数字是，接下来是和项数有关的两项的乘积，即n(n+1)，故答案为

例2(2015年高考山东卷)观察下列各式：

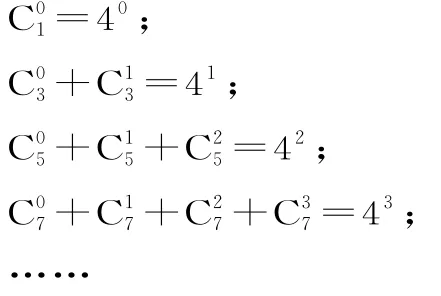
照此规律，当n∈N时：

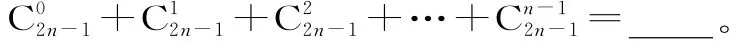
【命题立意】本题涉及了合情推理与组合知识，重点考查了同学们对合情推理的理解与运用，意在考查同学们观察、分析、归纳、推理判断的能力。解题的关键是能从前几个特殊的等式中观察、归纳、总结出一般规律，从而得到结论，此题属基础题。

【思路点拨】(1)合情推理；(2)组合数。

解析：第一个等式的右端为40=41-1；第二个等式的右端为41=42-1；第三个等式的右端为42=43-1，由此推理：第n个等式的右端为4n-1。

考向2：演绎推理

考情聚焦：(1)近几年高考，证明题不可或缺，不少证明过程主要是通过演绎推理来进行的；(2)此类试题主要以解答题的形式呈现，属中、高档题。

考向链接：演绎推理是由一般到特殊的推理，数学的证明过程主要是通过演绎推理进行的，只要采用的演绎推理的大前提、小前提和推理形式是正确的，其结论就一定正确，一定要注意推理过程的正确性与完备性。

例3数列{an}的前n项和记为Sn，已知

(2)Sn+1=4an。

【命题立意】本题主要考查利用演绎推理的方法解决数列问题。

【思路点拨】根据演绎推理“三段论”及数列相关知识求解。

解析：(1)因为an+1=Sn+1-Sn，an+1=所以(n+2)Sn=n(Sn+1-Sn)，即n Sn+1=2(n+1)Sn。

(大前提是等比数列的定义)

a2=3S1=3，S2=a1+a2=1+3=4=4a1。(小前提)

故对于任意正整数n，都有Sn+1=4an。(结论)

例4(2016年课标卷)有三张卡片，分别写有1和2，1和3，2和3。甲，乙，丙三人各取走1张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是2”；乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是1”；丙说：“我的卡2片上的数字之和不是5”。则甲的卡片上的数字是____。

【命题立意】本题主要考查利用演绎推理的方法解决实际问题。

【思路点拨】根据演绎推理、综合推理可得。

解析：由题意可知甲的卡片上的数字为1和3，乙的卡片上的数字为2和3，丙的卡片上的数字为1和2。

答案为1和3。

考向3：直接证明与间接证明

考情聚焦：(1)直接证明与间接证明是数学证明的两种思维方式，考查了同学们的逻辑思维能力，近几年高考对此部分的考查有所加强；(2)此类试题多以解答题的形式呈现，属中档题目。

例5已知集合Sn={X|X=(x1，x2，…，xn)，xi∈{0，1}，i=1，2，…，n}(n≥2)对于A=(a1，a2，…，an)，B=(b1，b2，…，bn)∈Sn，定义A与B的差为A-B=(|a1-b1|，|a2-b2|，…，|an-bn|)；A与B之间的距离为

(1)当n=5时，假设A=(0，1，0，0，1)，B=(1，1，1，0，0)，求A-B，d(A，B)；

(2)证明：∀A，B，C∈Sn，有A-B∈Sn，且d(A-C，B-C)=d(A，B)；(3)

证明：∀A，B，C∈Sn，d(A，B)，d(A，C)，d(B，C)三个数中至少有一个是偶数。

【命题立意】本题属于创新题，考查同学们运用新知识的能力，本题情景是全新的，对同学们的“学习能力”提出了较高要求。

解析：(1)A-B=(|0-1|，|1-1|，|0-1|，|0-0|，|1-0|)=(1，0，1，0，1)。

d(A，B)=|0-1|+|1-1|+|0-1|+|0-0|+|1-0|=3。

(2)设A=(a1，a2，…，an)∈Sn，B=(b1，b2，…，bn)∈Sn，C=(c1，c2，…，cn)∈Sn。

因为ai，bi∈{0，1}，所以|ai-bi|∈{0，1}(i=1，2，…，n)。

从而A-B=(|a1-b1|，|a2-b2|，…，|an-bn|)∈Sn。

由题意知ai，bi，ci∈{0，1}，i=1，2，…，n。

当ci=0时，||ai-ci|-|bi-ci||=|ai-bi|；

当ci=1时||ai-ci|-|bi-ci||=|(1-ai)-(1-bi)|=|ai-bi|。

所以d(A-C，B-C)= ∑n i=1|ai-bi|=d(A，B)。

(3)设A=(a1，a2，…，an)∈Sn，B=(b1，b2，…，bn)∈Sn，C=(c1，c2，…，cn)∈Sn。

设d(A，B)=k，d(A，C)=l，d(B，C)=h。

记0=(0，0，…，0)∈Sn，由(2)可知：

d(A，B)=d(A-A，B-A)=d(0，BA)=k。

d(A，C)=d(A-A，C-A)=d(0，CA)=l。

d(B，C)=d(B-A，C-A)=h。

所以|bi-ai|(i=1，2，…，n)中1的个数为k，|ci-ai|(i=1，2，…，n)中1的个数为l。

设t是使|bi-ai|=|ci-ai|=1同时成立的i的个数，则h=l+k-2t。

由此可知，k，l，h三个数不可能都是奇数，即d(A，B)，d(A，C)，d(B，C)三个数中至少有一个是偶数。

【总结升华】(1)有关否定性结论的证明常用反证法或举出一个结论不成立的例子即可；

(2)综合法和分析法是直接证明常用的两个方法，我们常用分析法寻找解决问题的突破口，然后用综合法来写证明过程，有时分析法和综合法要交替使用。

考向4：数学归纳法

考情聚焦：(1)新课标区对数学归纳法的考查有加强的趋势，应该引起同学们足够的重视；(2)此类试题多以解答题的形式呈现，属中档题。

例6等比数列{an}的前n项和为Sn，已知对任意的n∈N+，点(n，Sn)均在函数y=bx+r(b＞0且b≠1，b，r均为常数)的图像上。

(1)求r的值；

(2)当b=2时，记bn=2(l o g2an+1)(n∈N+)，证明：对任意的n∈N+，不等式成立。

【命题立意】考查数学归纳法。

解析：(1)因为对任意的n∈N+，点(n，Sn)，均在函数y=bx+r(b＞0且b≠1，b，r均为常数的)图像上，所以Sn=bn+r。

当n=1时，a1=S1=b+r；

当n≥2时，an=Sn-Sn-1=bn+r-(bn-1+r)=bn-bn-1=(b-1)bn-1。

又因为{an}为等比数列，所以r=-1，公比为b，an=(b-1)bn-1。

(2)当b=2时，an=(b-1)bn-1=2n-1，bn=2(l o g2an+1)=2(l o g22n-1+1)=2n。

①当n=1时，左边=，右边

②假设当n=k时不等式成立，即成立。

则当n=k+1时，左边

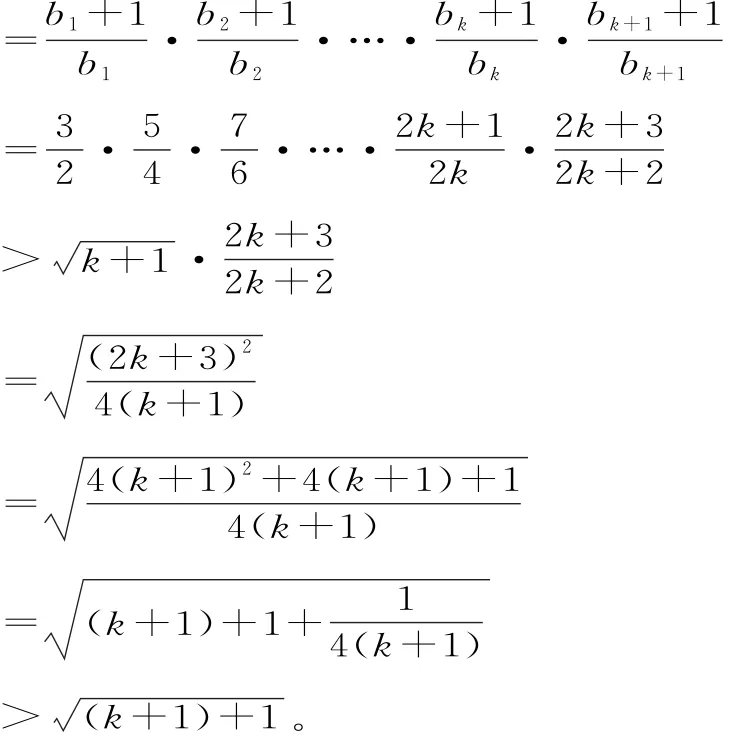
所以当n=k+1时，不等式也成立。

由①、②可得不等式恒成立。

【总结升华】(1)用数学归纳法证明与正整数有关的一些等式，解题的关键在于“先看项”，弄清等式两边的构成规律，等式的两边各有多少项，项的多少与n的取值是否有关，由n=k到n=k+1时等式的两边会增加多少项，增加了什么项。

(2)在本例证明过程中，①考虑“n取第一个值的命题形式”时，需认真对待，一般情况是把第一个值代入，判断命题的真假，②在由n=k到n=k+1的递推过程中，必须用归纳假设，不用归纳假设的证明就不是数学归纳法。

(3)在用数学归纳法证明的第二个步骤中，突出了两个“凑”字，一“凑”假设，二“凑”结论，关键是明确n=k+1时证明的目标，充分考虑由n=k到n=k+1时，命题形式之间的区别和联系。

【规律总结】

1.合情推理重在“合情”，要求结论符合“情理”，包括归纳推理与类比推理。归纳推理是由部分得到整体的一种推理模式；类比推理是由此及彼的推理模式；演绎推理是一种严谨的证明方式。

2.直接证明的最基本的两种证明方法是综合法和分析法，这两种方法也是解决数学问题时常见的思维方式。在实际解题时，通常先用分析法寻求解题思路，再用综合法有条理地表述解题过程。

3.数学归纳法是证明与正整数有关的数学命题的一种方法，在遇到与正整数有关的数学命题时，要考虑是否可以使用数学归纳法进行证明。

(1)在证明过程中突出两个“凑”字，即一“凑”假设，二“凑”结论，首先在证明n=k+1时要用上n=k时的假设，其次要明确n=k+1时证明的目标，充分考虑由n=k到n=k+1时，命题形式之间的区别和联系，化异为同，中间的计算过程千万不能省略。

(2)注意“两个步骤、一个结论”一个也不能少，切忌忘记归纳结论。