导数易错题归类辨析

■河南省罗山高中老校区 沈丽红

导数是求解曲线的切线方程、函数的单调性、极值(最值)等问题的有力工具，但有不少同学在学习导数时，常常因为对导数的概念及相关理论理解不到位而出现一些错误，下面就常见的易错点进行归纳，以供参考。

一、对导数的概念理解不透彻

例1已知f(x)在x=x0处的导数为4，则

错解：由已知有f'(x0)=4，所以

正解：

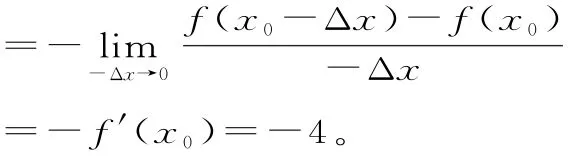
辨析：错解没有注意到本例中的增量是(x0-Δx)-x0=-Δx，而分母是Δx，两者不同，因为忽视了这一点，所以得出了错误答案4。

解此类问题时，应该注意在导数的概念中，增量的形式是多种多样的，但是无论哪种形式，一定要保证分子中自变量的增量与分母中的增量一致。

练习1：设f(x)为可导函数，且满足则函数y=f(x)在x=1处的导数为____。

正解：由题得函数y=f(x)在x=1处的导数

故答案为-1。

二、对导数的几何意义理解有误区

例2求过曲线f(x)=x3-2x上的点P(1，-1)的切线方程。

错解：由已知得，f'(x)=3x2-2，所以f'(1)=1。

故所求切线方程为y+1=1×(x-1)，即x-y-2=0。

正解：设切点坐标为 (x0，y0)，因为f'(x)=3x2-2，所以f'(x0)=3-2，且y0=f(x0)=-2x0，所以切线方程为yy0=(3-2)(x-x0)，即y-(-2x0)=(3-2)(x-x0)，又因切线过点(1，-1)，故-1-(-2x0)=(3-2)(1-x0)，即2-3+1=0，解得x0=1，或

故所求切线方程为x-y-2=0，或5x+4y-1=0。

辨析：出错的原因是直接把点P当作切点，来求解切线方程。混淆了“在某点处的切线”和“过某点处的切线”。“在某点处的切线”中该点一定是切点，但对于“过某点处的切线”中该点不一定是切点，故应先设出切点，再利用该点在切线上来确定切点坐标，进而求出切线方程。

练习2：已知曲线f(x)=2x2+3，过点(2，9)作曲线f(x)的切线，求切线的方程。

正解：设切点坐标为(x0，y0)，由已知得f'(x)=4x，则f'(x0)=4x0，且y0=f(x0)=2+3，所以切线方程为y-(2+3)=4x0(x-x0)，又切线过点(2，9)，所以有9-(2+3)=4x0(2-x0)，即2-8x0+6=0，解得x0=1或x0=3，故所求切线方程为4x-y+1=0或12x-y-15=0。

三、对导数与函数的单调性的关系理解不全面

例3已知函数f(x)=x3+x2-a x-1在区间[1，+∞)内单调递增，求实数a的取值范围。

错解：因为函数f(x)=x3+x2-a x-1在区间[1，+∞)内单调递增，所以f'(x)=3x2+2x-a＞0在[1，+∞)上恒成立，即3x2+2x＞a在[1，+∞)上恒成立。

又y=3x2+2x在[1，+∞)上单调递增，所以y=3x2+2x≥5，故a＜5。

正解：因为函数f(x)=x3+x2-a x-1在区间[1，+∞)内单调递增，所以f'(x)=3x2+2x-a≥0在[1，+∞)上恒成立，即3x2+2x≥a在[1，+∞)上恒成立。

又y=3x2+2x在[1，+∞)上单调递增，所以y=3x2+2x≥5，所以a≤5，经检验a=5时，在区间[1，+∞)内f'(x)=3x2+2x-5=(3x+5)(x-1)≥0，且只有f'(1)=0。

此时函数f(x)=x3+x2-a x-1在[1，+∞)上仍然单调递增，故a=5符合题意，故a的取值范围为(-∞，5]。

辨析：错因是误认为f'(x)＞0是y=f(x)在区间[1，+∞)内单调递增的充要条件。实际上，在某区间Ι内f'(x)＞0(f'(x)＜0)是函数y=f(x)在区间Ι内单调递增(递减)的充分不必要条件。如果在区间Ι内出现“个别点”使得f'(x)=0，不会影响函数f(x)在该区间内的单调性。简而言之，f(x)在区间Ι内递增(递减)的充要条件是对任意x∈Ι，有f'(x)≥0(f'(x)≤0)(但是这里满足f'(x)=0的点应只是在个别点处，也就是说在区间Ι内f'(x)不能恒等于0)。

练习3：已知函数在区间(-2，+∞)内单调递减，则实数a的取值范围为____。

正解：由题意得，在(-2，+∞)内恒成立，所以解不等式得但当时，恒成立，不合题意，应舍去，故

四、错误理解“f'(x0)=0”与“f(x)在x0处有极值”的关系

例4已知函数f(x)=x3-a x2-b x+a2在x=1处有极值10，则的值为( )。

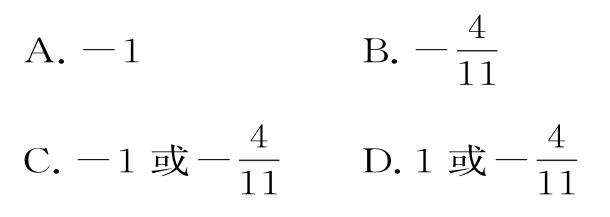
错解：由题意知f'(x)=3x2-2a x-b，f'(1)=0，f(1)=10。

正解：由题意知f'(x)=3x2-2a x-b，f'(1)=0，f(1)=10。

A.0 B.1 C.2 D.3

正解：y'=x3-x2=x2(x-1)，令y'=0，得x=0或x=1。

当x变化时，y'，y的变化情况如表1所示。答案为B。

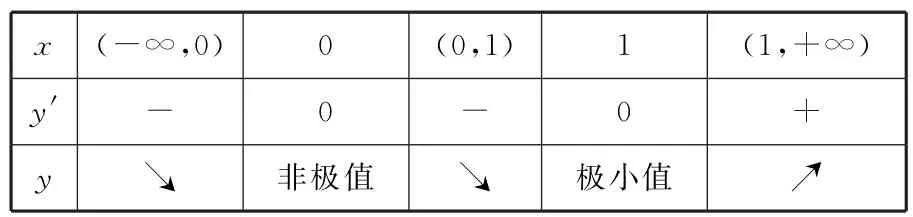
表1

辨析：根据极值的定义可知，对于一个可导函数f(x)，如果函数y=f(x)在x0处有极值，则一定有f'(x0)=0，但是若有f'(x0)=0，则点x0不一定是函数y=f(x)的极值点，即f'(x0)=0只是f(x)在x0处有极值的必要条件。所以若函数y=f(x)在点x0处取得极值，不仅要有f'(x0)=0，且f'(x0)在x0左右两侧的符号应该不同，故解此类题时，应检验所求参数的值是否符合题意。

练习4：函数

故该函数有一个极值点。答案为B。