高慧明老师讲数学（2）——空间向量的妙用（上）

■北京市第十二中学 高慧明

本刊特邀栏目专家简介：

高慧明首届全国十佳班主任，北京市高中数学特级教师，国家教育部课程改革“全国先进工作者”，全国著名高考数学命题与考试研究专家，国家教育部“国培计划”全国中小学教师培训和班主任培训特邀主讲专家，受邀为教育部“国培计划”做有关高中数学课堂教学、班级管理、教师专业成长等专题报告多场，在全国引起强烈反响。出版个人专著《高考数学命题规律与教学策略》《高中数学思想方法及应用》《让高中生学会学习》《高慧明班级高效管理艺术》《高慧明数学教学实践与研究》(丛书)等多部，应邀主编、参编教材和教学著作30余部。

立体几何是高中数学的重点内容，是体现求解能力和空间想象能力的重要载体。空间向量的引入，给立体几何问题的解决带来了全新的解题思路，有效地减少了繁杂的空间想象和几何推理。借助空间向量解决立体几何解答题常涉及证明(判断)线、面位置关系，求解空间角，确定几何元素(通常为点)的确切位置等问题。

一、利用空间向量证明（判断）线、面位置关系

例1如图1，已知在几何体A B C D E F中，底面A B C D为正方形，A E=2B F=4，A E⊥平面A B C D，A E∥B F。

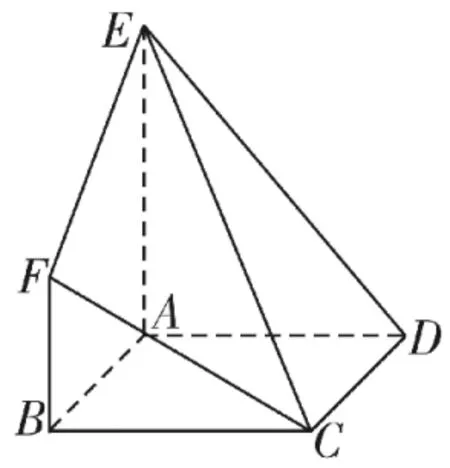
图1

(1)证明：F C∥平面A E D。

(2)若二面角E-F C-B的余弦值为，求该几何体A B C D E F的体积。

分析：根据图形建立空间直角坐标系，找出直线F C的方向向量和平面A E D的法向量通 过 计 算 求 得，进而可证得结果。

解析：(1)以A为原点分a，-2)。

易知A B⊥平面A E D，可取别为x，y，z轴的正方向，建系如图2，设A B=a。

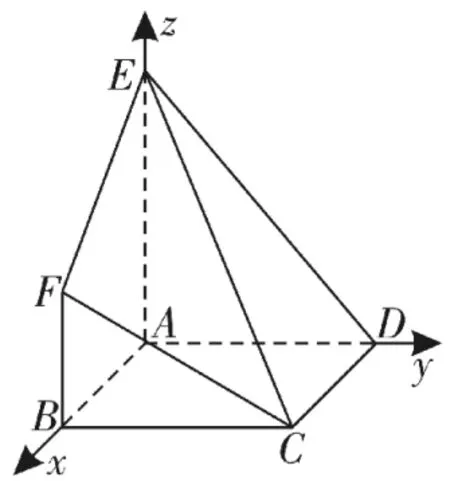
图2

方法一：有C(a，a，为平面A E D的法向量。

方法二：因为A E⊥平面A B C D，A E∥B F，B C∥A D，B C∩B F=B，A E∩A D=A，所以平面B C F∥平面A E D。

又C F⊂平面B C F，所以C F∥平面A E D。

(2)在(1)的空间直角坐标系中，有B(a，0，0)，C(a，a，0)，F(a，0，2)，E(0，0，4)。

易知A B⊥平面B F C为平面B F C的法向量。

设n=(x，y，z)为平面E F C的法向量，则⇒n=(2，2，a)。

设二面角E-F C-B的大小为θ，则有

点评：在利用空间向量证明直线l与平面α平行时，可利用直线的方向向量与平面α的法向量垂直，证得结果。在证明线、面位置关系时，向量法与几何法相比显得更为直接，特别是在证明较为复杂的线、面位置关系时，向量法的优势更加明显。

例2如图3，四边形A B C D中，A C⊥B D，C E=2A E=2B E=2D E=2，将四边形A B C D沿着B D折叠，得到图4所示的三棱锥A-B C D，其中A B⊥C D。

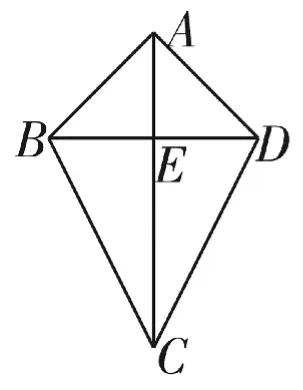
图3

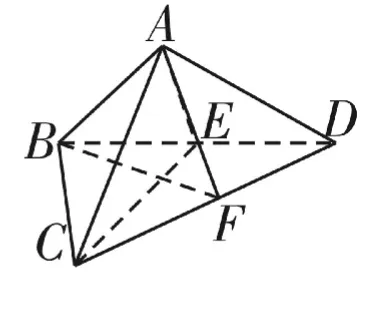
图4

(1)证明：平面A C D⊥平面B A D；

(2)若F为C D的中点，求二面角CA B-F的余弦值。

分析：对于(1)，利用题中条件，合理建立空间直角坐标系，求解平面A C D和平面B A D的法向量，利用两法向量之积为0，证得平面A C D⊥平面B A D。

解析：(1)(方法一)以E为原点，以的方向为x轴 正 方 向的方向为y轴正方向，建立如图5所示的空间直角坐标系。

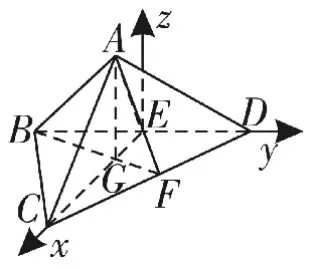
图5

过A点作平面B C D的垂线，垂足为G，根据对称性，显然G点在x轴上，设A G=h。

由题设条件可得下列坐标：E(0，0，0)，C(2，0，0)，B(0，-1，0)，D(0，1，0)，

由于A B⊥C D，所 以解得

则A点坐标为故

设平面A B D的法向量为m=(x1，y1，z1)。

设平面A C D的法向量为n=(x2，y2，z2)。

所以平面A C D⊥平面B A D。

(方法二)因为A E⊥B D且B E=D E=A E，可得△A B D为等腰直角三角形。

则A B⊥A D，又A B⊥C D，且A D、C D⊂平面A C D，A D∩C D=D，故A B⊥平面A C D。

又A B⊂平面B A D，所以平面A C D⊥平面B A D。

由于A D⊥A B，A D⊥A C，则为平面A B C的一个法向量。

因为二面角C-A B-F为锐角，则二面角C-A B-F的余弦值为

二、利用空间向量求解空间角

例3如图6，在三棱柱A B C-A1B1C1中，B A=B C=B B1，∠A B C=90°，B B1⊥平面A B C，点E是A1B与A B1的交点，点D在线段A C上，B1C∥平面A1B D。

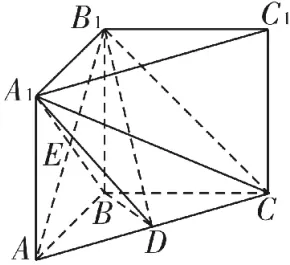
图6

(1)求证：B D⊥A1C；

(2)求直线A1C与平面A1B1D所成的角的正弦值。

分析：(1)连接E D，根据题中条件求得B D⊥A C，再由A A1⊥平面A B C，证得B D⊥平面A A1C1C，根据线与线垂直的判定证得B D⊥A1C。(2)根据三棱柱的特点建立空间直角坐标系，然后确定A1C的方向向量与平面A1B1D的法向量，求出两个向量的夹角的余弦值，此余弦值的绝对值即为直线与平面所成角的正弦值。

解析：(1)如图7，连接E D，因为平面A B1C∩平面A1B D=E D，B1C∥平面A1B D，所以B1C∥E D。

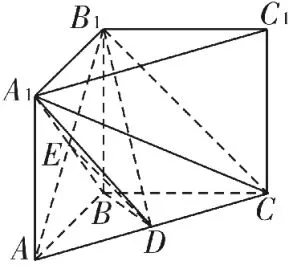
图7

因为E为A B1的中点，所以D为A C的中点，因为A B=B C，所以B D⊥A C。

由A A1⊥平面A B C，B D⊂ 平 面A B C，得A A1⊥B D。

又A A1、A C是平面A A1C1A内的两条相交直线，得B D⊥平面A A1C1C。

因为A1C⊂平面A A1C1C，所以B D⊥A1C。

(2)令A B=1，则B C=B B1=1，如图8，以B为坐标原点，建立空间直角坐标系B-x y z，则A1(1，0，1)，B1(0，0，1)，C(0，1，0)，

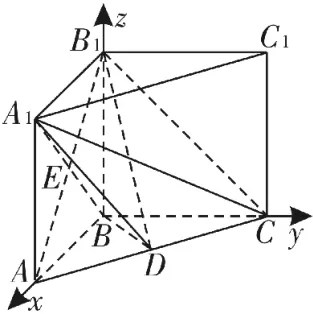
图8

设m=(x，y，z)是平面A1B1D的一个法向量，

令z=1，得m=(0，2，1)。设直线A1C与平面A1B1D所成的角为θ。

点评：利用空间向量求解直线l与平面α所成角时，一定要厘清概念，避免将直线l的方向向量与平面α的法向量的夹角当作直线l与平面α所成的角。

(未完待续)