例谈向量数量积的解题策略*

江苏省无锡市第六高级中学(214023) 孙艳秋

江苏省无锡市运河实验中学(214023) 韩郡

向量的本身特点告诉我们处理向量问题可以从几何角度和代数角度入手.

一、解题策略探究

1.从几何角度入手

1.1 基底表示法

平面向量基本定理告诉我们：平面内两不共线向量可以表示平面内任一向量.从函数中的变量个数角度考虑，也希望向量的个数越少越好，因此不共线的两向量作为基底，表示题干中所求的向量(已知表未知思想)，可以达到化繁为简的目的.

图1

例1(2014年高考江苏卷第12 题)如图1，在平行四边形ABCD中，已知AB=8,AD=则的值是____.

分析在平行四边形中我们一般选择相邻两边作为基底，因此本题我们选择作为基底.

解因为所以所以因为所以所以所以

小结1基底表示法选择基底很重要，但很多同学在选择基底时比较混乱.通常我们以特殊图形如平行四边形，矩形，直角梯形，等腰、等边三角形等的相邻两边作为基底，或者以题目中已知的两线段作为基底.

1.2 定义投影法

向量数量积定义，要求两非零向量a,b数量积用a·b表示，即a·b=|a||b|cos〈a,b〉，其中|b|cos〈a,b〉表示向量b在向量a方向上的投影.所以a·b的几何意义就是其中一个向量在另一个向量方向上的投影长度与另一个向量模长的乘积.

例2(2018 届无锡市高三期中第12 题)如图2 所示，在平行四边形ABCD中，AP⊥BD，P为垂足，且AP=1，则=____.

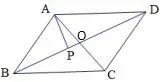
图2

分析设AC与BD交于点O，因为AP⊥BD，所以在方向上的投影长度就等于AP，所以又因为O为AC中点，所以

小结2根据投影法的定义，当我们要求的数量积的两向量为直角三角形的斜边与直角边，或者等腰三角形的腰与底边时，或者求范围时其中一向量模长为定值时，我们常常考虑采用投影法求.

图3

1.3 极化恒等式法

初中代数中有一个常用的恒等式：4ab=(a+b)2-(a-b)2，它由两个完全平方公式相减而成.而今在高中向量中有一个类似的恒等式：4ab=(a+b)2-(a-b)2，称之为极化恒等式.它有如下几何意义：如图3，在△ABC中，点D为BC的中点，则

图4

例3(镇江市2017 届高三上学期期末)已知椭圆1(m＞n＞0)的左、右焦点分别为F1,F2，P是以椭圆短轴为直径的圆上任意一点，则

分析如图4，利用极化恒等式，OF21=b2-c2，a2=m，b2=n，所以c2=m-n，所以

小结3极化恒等式法是解决共起点数量积的强有力的手段，能够把共起点的两向量转化成第三边与第三边中线长的代数关系，快速简化问题.因此，当我们看到题目中已知或能求出第三边的长，或者第三边中线长时，可以考虑采用极化恒等式快速解决问题.

2.从代数角度入手

2.1 建系法有人说建系法是万能的，建系法是将几何问题代数化的有力手段，可以把复杂的几何关系代数化，转化成代数运算，大大降低试题的难度，是数形结合思想的最直接体现.

例4(2017年高考江苏卷第12 题)如图5，在同一个平面内，向量的模分别为与的夹角为α，且tanα=7，与的夹角为45°.若则m+n=_____.

图5

图6

分析因为向量的模分别为与的夹角为45°是特殊角，所以考虑 以O为原点，OC方向为x轴正半轴，垂直于OC为y轴，建立直角坐标系，如图6.因为tanα=7，所以所以所以m+n=3.

小结4一般当我们遇到特殊角如30°,45°,60°,90°,120°,135°,150°等特殊角，以及一些特殊图形如直角、等腰、等边三角形，矩形、菱形，正方形时考虑建系法.

二、高考运用

真题(2016年高考江苏卷第13题)如图7，在△ABC中，D是BC的中点，E,F是AD上的两个三等分点，则的值是____.

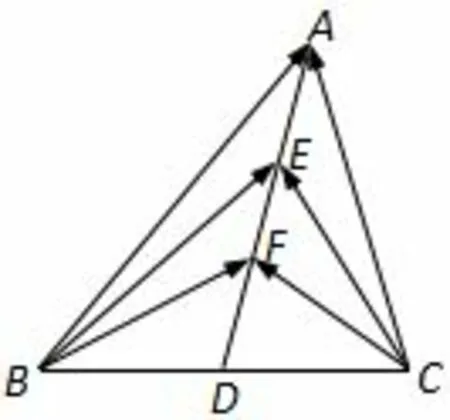
图7

分析此题作为江苏高考的一道填空压轴题，但是得分率却不高，主要还是很多学生不知道如何下手.因为D是BC的中点，题目中涉及到的向量的终点A,E,F均在AD上，因此可以选择作为基底，采用基底法处理.因为均是共起点数量积问题，而且出现了第三边中点，因此也可以利用极化恒等式法解决.从题干信息中看出，本题没有对△ABC形状做出特殊限定，因此我们可以假设△ABC为等腰三角形，所以可以采用特殊化建系法.

法1(基底表示法)因为且所以所以同理所以

法2(极化恒等式法)因为所以所以

法3 (建系法)假定△ABC为等腰三角形，以底边BC为x轴，BC边上的高为y轴，建立直角坐标系.设A(0,b)，B(-a,0)，C(a,0)，D(0,0)，则所以所以所以所以

三、结束语

数学题目千变万化，唯有抓住问题的本质，才可以以不变应万变.在我们学习与教学中，只有学会从问题的次数、系数、结构形式、位置特征等方面观察问题，总结对应方法，才可能避免题海战术，体会到数学解题的乐趣.