例说求数量积的取值范围(最值)求解策略*

福建省龙海第一中学(363100) 苏艺伟

数量积是向量的重要内容，求数量积的取值范围或最值问题经常出现在向量试题中.此类试题不仅有一定的难度且较为灵活，无固定的解法，在实际解题中根据题目条件综合运用数量积的相关知识，灵活选取恰当的解题策略，方能出奇制胜，顺利求解.

策略1直接运用数量积的代数形态

数量积的代数形态指的是a·b=|a|·|b|·cosθ，通常借助代数形态进行数量积的相关运算.

例1已知a,b满足|a|=2，a2+2a·b+2b2=8，求a·b的取值范围.

解析设|b|=x，〈a,b〉=θ.由已知有a2+2a·b+2b2=8.整理得cosθ=令得故

简评借助数量积的代数形态反解出cosθ，利用余弦函数的有界性得到x的取值范围，从而求出a·b的取值范围.

例2已知圆C:(x-2)2+y2=4，圆M:(x-2-5 cosθ)2+(y-5 sinθ)2=1.过圆M上任意一点P作圆C的两条切线PE，PF，切点分别为E,F，求的最小值.

解析

显然当点P在圆M上运动时，|PC| ∈[4,6].令t=|PC|2，则t ∈[16,36].故因此当t=12时，有最小值6.

简评借助数量积的代数形态将表示成PE·PF ·cos ∠EPF，借助圆的切线的几何性质求解.

策略2运用数量积的几何形态

数量积的几何形态是建立在投影的基础上.a·b表示|a|乘以b在a上的投影，也可以表示|b|乘以a在b上的投影.

例3同例1.______

图1

解析由a2+2a·b+2b2=8得+a · b+b2=4，即b2+a·b=2，即整理得记则b的终点B在以C为圆心，为半径的圆上.a·b表示|a|乘以b在a上的投影.如图1 所示，当点B在E处时，投影最大，为当点B在F处时，投影最小，为所以

简评上述解法利用数量积的几何形态，抓住投影这个关键定义，首先结合图形求出投影的范围，从而得到a·b的取值范围.

策略3 运用数量积的恒等形态

由数量积的恒等形态可以得到数量积的极化公式，它将数量积问题转化成为两条线段的平方差问题，可以有效地处理数量积的取值范围问题.

例4已知△ABC是边长为2 的等边三角形，P为面ABC内一点，求的最小值.

解析取BC中点M，AM中点N，则所以因此的最小值是

简评运用恒等形态将转化成为PN2-MN2.

例5已知正△ABC内接于半径为2 的圆O，点P是圆O的一个动点，求的取值范围.

解析由已知可得正△ABC的边长为取AB中点D，则当点P位于C处时，PD最大，为3；当点P位于CD延长线与圆交点时，PD最小，为1.因此，

简评运用恒等形态将转化成为PD2-BD2.

策略4运用不等式的性质

借助不等式的重要性质可以求出数量积的取值范围(最值)，如三角不等式，柯西不等式，重要不等式.

例6已知a,b满足|a|=2|b|，|a-b|=2，求a·b的取值范围.

解析由|a - b|=2 得a2-2a · b+b2=4，即4|b|2-2a·b+|b|2=4，解得a·b=记|b|=t，则由||a|-|b||≤|a+b|≤|a|+|b|，得|b|≤2 ≤3|b|，即因此

简评首先将a·b表示成为然后借助向量中的三角不等式求出|b|的取值范围，从而得出a·b的取值范围.

例7已知a,b满足|a|=1,|b|=2，若对任意单位向量e均有求a·b的最大值.

解析|(a+b)·e|≤|a·e|+|b·e|由e的任意性可知，故有a2+2a·b+b2≤6，从而有因此a·b的最大值为

简评借助向量中的三角不等式以及e的任意性得到√从而求出a·b的最大值为

例8已知a,b,c满足，且|a|+|b|+|c|=4.求c·(a+b)的最大值.

解析由已知可得〈a,c〉=60°，〈b,c〉=60°，c·(a+b)=因此c·(a+b)的最大值为2.

简评借助重要不等式ab≤求出c·(a+b)的最大值为2.

例9在△ABC中，已知∠C=90°，AC=4，BC=3，D是AB中点，E,F分别是BC,AC上的动点，且EF=1，.求的最小值.

解析以C为原点建立平面直角坐标系.设C(0,0)，其中a2+b2=因此又(4a+3b)2≤(16+9)(a2+b2)，即(4a+3b)2≤25，所以-5 ≤4a+3b≤5，故

简评借助柯西不等式求出4a+3b的最值，从而求出的最小值.

下面给出几道练习：

1.已知a和单位向量b满足|a+2b|=2|a-b|，求a·b的取值范围.

解析1由|a+2b|=2|a-b|两边同时平方得a·b=所以结合cosθ ∈[-1,1]得|a| ∈[0,4].故a·b=|a|·|b|·cosθ=

解析2设且O(0,0)，B(1,0)，A(x,y).则a+2b=(x+2,y)，a-2b=(x-1,y).由|a+2b|=2|a-b|得化简得(x-2)2+y2=4.故a的终点A在以(2,0)为圆心，2 为半径的圆上运动，所以x ∈[0,4].a·b=(x,y)·(1,0)=x ∈[0,4].

2.已知a,b满足a·b=0，且|a-b|=|a-2c|=2，求a·c的取值范围.

解析1设且A(a,0)，B(0,b).由|a-b|=2 得a2+b2=2.由|a-2c|=2 得a2-4a·c+4c2=4，即a2-4a·c+(2|c|cosθ)2+(2|c|sinθ)2=4.整理得(|a|-2|c|cosθ)2+(2|c|sinθ)2=4，所以(|a|-2|c|cosθ)2≤4.由-2 ≤|a|-2|c|cosθ≤2，得-2|a|≤|a|2-2a·c≤2|a|，即|a|2-2|a|≤2a·c≤|a|2+2|a|.结合|a| ∈[-2,2]得

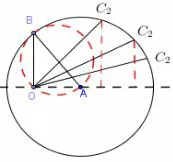
图2

解析2记2c，=b，则点O在以AB为直径的小圆上运动，2c的终点C2在以A为圆心，2 为半径的圆大圆上运动.与的数量积即为图(2)中与在上的投影的乘积.先让C2在以A为圆心，2 为半径的圆大圆上运动，发现当与同向时，取到最大值；再让点O在以AB为直径的小圆上运动，发现当O运动到B时，取到最大值为8；取到最小值时，必定有与反向.又因为由基本不等式知，当且仅当O在的中点时，取到最小值，所以

通过上述试题及其分析，不难看出，对于数量积取值范围(最值)问题，应充分运用数量积的代数形态，几何形态，恒等形态，结合不等式的重要性质求解.对于有些试题还要灵活观察图形，借助几何直观方能顺利求解.