函数与导数模块第二轮复习备考建议

湖北省华中师范大学第一附属中学(430223) 张 丹

广东省华南师范大学数学科学学院(510630) 张雨桐

函数与导数模块在高考中占有比较大的比重，是高中数学学习的一个重点和难点.在高三二轮复习中，有针对性的做好该模块的复习备考，以期达到事半功倍的效果.

一、全国新课标I 卷近三年高考考点及分析

表1：全国I 卷近三年函数与导数的考点

考点分析全国新课标I 卷对函数与导数的考查比较稳定，一般为两个小题和一个大题，但是2018年文理科都是三个小题和一个大题.

小题主要考查：函数的单调性、奇偶性、对称性、指数函数与对数函数的性质；函数的零点、导数的几何意义、函数的极值与最值、函数的图象及变换、数形结合思想等，试题难度一般是：一道中档题，一道压轴题.

大题主要考查：导数的几何意义函数单调性、极值点、最值、参数范围、函数零点、导数与不等式，注重考查函数与方程、化归与转化、分类与整合等数学思想方法，还综合考查了运算求解能力、推理论证能力、抽象概括能力等，常常作为压轴题出现，难度较大.

二、高三二轮复习备考建议

1.重视基础抓好两条主线，构建函数知识网络.一是“基本函数的概念与性质”，熟练掌握函数的定义域、解析式、值域、奇偶性、单调性、周期性、对称性等基本知识及求解方法，并会灵活应用；二是“基本函数的图象与性质”，要熟练掌握一次函数、二次函数、反比例函数、指数函数、对数函数等常用函数的图象以及图象变换，会运用基本初等函数的图像分析函数的性质，会利用导数研究图象的特征、研究方程根(函数的零点)及其性质.

2.强调能力从对近几年全国卷函数与导数的高考试题分析，充分体现高考命题强调“以能力立意”的指导思想，全国高考对函数与导数的考查重在对函数与导数知识理解的准确性、深刻性，综合考查用函数与方程思想、转化与化归思想、分类与整合思想，还综合考查运算求解能力、推理论证能力、抽象概括能力，并且是多种能力同时考查.因此，在对“函数与导数”二轮复习中，既要突出基础性，还要关注综合性，对优秀学生(尤其是尖子生)强化思想方法的训练，要善于转化命题，引进变量构建函数，形成透过函数看问题的意识；加强训练学生“增加条件”，合理恰当分类；强化“由式到图”和“由图到式”的转化训练；关注学生的运算能力的训练，培养学生合理、准确的运算能力；注重数学思维能力的训练，在审题中能抓住思维起点，结合有关知识能够合乎逻辑地准确表述推理过程，训练推理论证能力.

3.抓好落实在“函数与导数”复习中，要准确理解概念、掌握通性通法，特别关注一些易错点，切实抓好落实.易错点主要有：

①求导公式使用不正确，导致整个题目计算错误；

②忽视函数的定义域，单调区间书写不规范；

③用几何直观代替证明，而没有严格的逻辑推理；

④构造函数不当，造成运算繁杂；

⑤分类讨论思路混乱，造成讨论不完整；

⑥片面、孤立的考虑问题，不能联系前后问进行难点突破.

4、寻求对策

①提高求导运算的准确性，特别是含有复合函数的求导和分式型函数的求导；

②注重分类讨论问题中，寻找分类依据的训练，做到不重不漏；

③数形结合，以“形”引导思维，寻找解题的途径；

④加强代数推理能力，严谨、合理的数学表述的培养；

⑤合理地对问题进行转化，抓住问题的本质；

⑥学会利用隐含条件和已证的结论，寻求问题突破口.

三、几种常见类型问题

题型一：导数的几何意义

导数的几何意义在高考中主要出现在小题和大题的第一问，难度较小.2016—2018年全国卷中导数的几何意义的考查情况见表3.

表3：2016—2018年导数的几何意义在全国卷的考查情况

函数y=f(x)在x0处的导数，就是曲线y=f(x)在点(x0,f(x0))处的切线的斜率.要注意曲线在某点处的切线与经过某点作曲线的切线的区别：

(1)已知y=f(x)在点(x0,f(x0))的切线方程为y-y0=f′(x0)(x-x0)；

(2)若求过点(a,b)的切线方程，应先设切点坐标为(x0,f(x0))，由y-y0=f′(x0)(x-x0)过点(a,b)，求得x0的值，从而求得切线方程，另外，要注意切点既在曲线上又在切线上.

例1(2016 全国II 卷理科第16 题)若直线y=kx+b是曲线y=lnx+2 的切线，也是曲线y=ln(x+1)的切线，则b=____.

解析设y=lnx+2 的切点为(x1,lnx1+2)，则它的切线为y=·x+lnx1+1，设y=ln(x+1)的切点为(x2,lnx2+2)，则它的切线为：所以解得所以b=lnx1+1=1-ln 2.

题型二：函数单调性的讨论与研究

近几年全国卷加大了利用导数研究函数单调性的考查力度，题型灵活多变，多出现在选择题与填空题的最后两题或解答题的21 题，难度较大，详情如下：

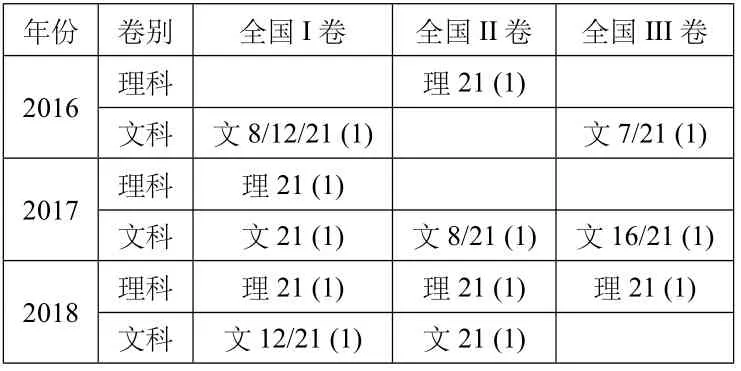
表4：2016—2018年函数单调性在全国卷的考查情况

判断函数的单调性一般有四种方法：定义法、图象法、复合函数单调性法和导数法.这里主要讨论和研究利用导数研究函数单调性.

1.函数单调性与导函数符号的关系：

一般地，在区间(a,b)内，如果f′(x)＞0，那么函数y=f(x)在该区间内单调递增； 如果f′(x)＜0，那么函数y=f(x)在该区间内单调递减.

2.求可导函数y=f(x)单调区间的一般步骤：

(1)确定函数y=f(x)的定义域；

(2)求y=f(x)的导函数f′(x)；

(3)讨论导函数的零点是否存在：若f′(x)≥0 (或f′(x)≤0)在定义域内恒成立，则所求函数在定义域内单调递增(或单调递减)； 若导函数存在多个零点，以零点分段，讨论各区间符号，一般以列表形式；

(4)写出函数y=f(x)的单调区间，当有多个单调区间时，中间用“，”隔开或用“和”字隔开.

注：使f′(x)=0 的离散点不影响函数的单调性，所以写函数的单调区间时，表示为开区间更为合适.

例2(2015 全国II 卷理科第12 题)设函数f′(x)是奇函数f(x)的导函数，f(-1)=0，当x＞0 时，xf′(x)-f(x)＜0，则使得f(x)＞0 成立的x的取值范围是( ).

A.(-∞,-1)∪(0,1) B.(-1,0)∪(1,+∞)

C.(-∞,-1)∪(-1,0) D.(0,1)∪(1,+∞)

解析由题意，设函数则g′(x)=因为当x＞0 时，xf′(x)-f(x)＜0，故当x＞0 时，g′(x)＜0，所以g(x)在(0,+∞)单调递减；又因为函数f(x)(x ∈R)是奇函数，故函数g(x)是偶函数，所以g(x)在(-∞,0)上单调递增，且g(-1)=g(1)=0.当0＜x＜1 时，g(x)＞0，则f(x)＞0； 当x＜-1 时，g(x)＜0，则f(x)＞0.综上所述，使得f(x)＞0 成立的x的取值范围是(-∞,-1)∪(0,1).故选A.

题型三：极值与最值问题

函数的极值与最值问题是高考的重要内容，详情如下：

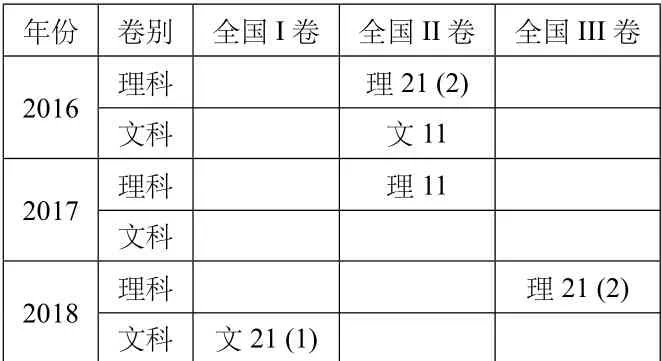
表5：2016—2018年极值与最值问题在全国卷的考查情况

1.利用导数研究函数的极值的解题思路：

(1)确定函数y=f(x)的定义域，并求出函数y=f(x)的导函数f′(x)；

(2)求导函数的零点；

(3)判断导函数的零点左右两侧导函数值的符号；

(4)利用结论写出极值.

2.求可导函数y=f(x)在闭区间[a,b]上的最值的解题思路：

(1)计算函数y=f(x)在开区间(a,b)内的所有驻点；

(2)计算函数y=f(x)在驻点和端点处的函数值；

(3)比较各数值大小，其中最大的一个为最大值，最小的一个为最小值.

3.求可导函数在开区间(a,b)上的最值的解题思路(这里只讨论“开区间内只有一个驻点”的情形)：

若函数在开区间(a,b)内只有一个驻点，判断该驻点左右两侧的符号：左正右负最大值，左负右正最小值.

注：(1)有关极值问题要从极值存在的充要条件上考虑，不仅要注意导数为零，同时也要注意导数为零附近两侧导数的变号情况； (2)驻点是指导函数的零点.

例3已知函数g(x)=f(x)+-bx，函数f(x)=x+alnx在x=1 处的切线l与直线x+2y=0 垂直.

(I)求实数a的值；

(II)若函数g(x)存在单调递减区间，求实数b的取值范围.

(III)设x1,x2(x1＜x2)是函数g(x)的两个极值点，若求g(x1)-g(x2)的最小值.

解析(I)因为f(x)=x+alnx，所以f′(x)=1+又因为函数在x=1 处的切线l与直线x+2y=0 垂直，所以k=y′|x=1=1+a=2，所以a=1.

(II)因为g(x)=lnx+-(b-1)x，所以g′(x)=由题知g′(x)＜0 在(0,+∞)上有解，设u(x)=x2-(b-1)x+1，则u(0)=1＞0，因为x＞0，所以只需解得b的取值范围是(3,+∞).

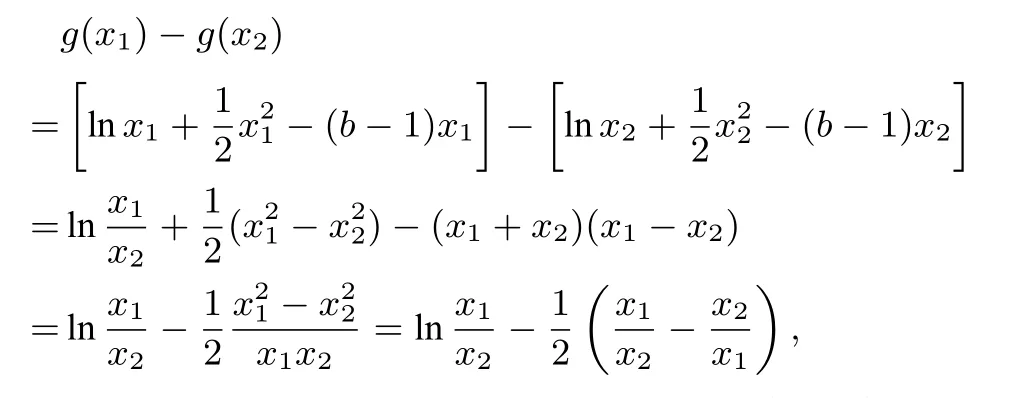
题型四：函数零点问题

函数零点问题本质上是考查函数的单调性，在小题通常中偏难，在大题为压轴题，详情如下：

表6：2016—2018年函数零点问题在全国卷的考查情况

问题类型主要有如下两类：

1.讨论含参函数的零点问题：

(1)解题方法：利用转化与化归思想，将函数的零点问题转化为两个函数图象的交点个数问题，特别地，有些函数可以将参变量和自变量分离，从而将零点问题转化为不含参数的函数与常数函数的交点个数问题.

(2)解题思路(数形结合思想)：

(i)将方程变形，使得等式左右两边的函数都比较容易求出单调区间，从而画出图象；

(ii)对等式左右两边的函数分别求出单调区间，并画出大致图象；

(iii)判断两个函数图象的交点个数，从而得到原函数的零点个数.

2.已知零点个数，求参数的取值范围：

(1)解题方法：通过对参数分类讨论，分情况研究函数的单调性和极值，进而确定函数的零点.由于要使用零点定理，在取特殊点判断其函数值的正负时，有时会用到放缩法等方法.

(2)解题思路：(i)将方程变形，确定要研究的函数； (ii)求出函数的导函数f′(x)，确定分类标准； (iii)在每一类中分别求出函数的单调区间和极值，进而讨论零点情况； (iv)下结论.

例4(2015 全国I 卷理科第21 题)已知函数f(x)=

(I)当a为何值时，x轴为曲线y=f(x)的切线；

(II)用min{m,n}表示m,n中的最小值，设函数h(x)=min{f(x),g(x)}(x＞0)，讨论h(x)零点的个数.

解析(I)设曲线y=f(x)与x轴相切于点(x0,0)，则f(x0)=0，f′(x0)=0，即解得因此，当时，x轴是曲线y=f(x)的切线.

(II)当x ∈(1,+∞)时，g(x)=-lnx＜0，从而h(x)=min{f(x),g(x)}≤g(x)＜0，所以h(x)在(1,+∞)无零点.

当x=1 时，若则f(1)=h(1)=min{f(1),g(1)}=g(1)=0，故x=1 是h(x)的零点；若则h(1)=min{f(1),g(1)}=f(1)＜0，故x=1 不是h(x)的零点.

当x ∈(0,1)时，g(x)=-lnx＞0，所以只需考虑f(x)在(0,1)的零点个数.

(i)若a≤-3 或a≥0，则f′(x)=3x2+a在(0,1)无零点，故f(x)在(0,1)单调，而所以当a≤-3 时，f(x)在(0,1)有一个零点；当a≥0 时，f(x)在(0,1)无零点.

(ii)若-3＜a＜0，则f(x)在单调递减，在单调递增，故当x=时，f(x)取得最小值，最小值为f

题型五：恒成立、能成立求参数范围问题

函数不等式恒成立、能成立求参数范围问题在高考中主要出现在第21 题第二问的位置，难度较大，详情如下：

表7：近三年恒成立、能成立求参数范围问题在全国卷的考查情况

1.解题方法：利用等价转化思想，将函数不等式恒成立、能成立问题转化为最值问题，从而求出参数范围.常用的方法主要有分离变量法和函数性质法(利用函数单调性).

2.解题思路：(1)能分离变量的先分离变量，若不含参数的函数最值容易求出，或者用洛必达法则能求出，就能得到参数的取值范围； (2)不好分离变量，或者分离变量之后不含参数的函数最值很难求出，则需要对原来的函数求导，再对参数进行讨论，利用函数的单调性，求函数的最值，从而得到参数范围.

例5(2015 全国II 卷理科第21 题)设函数f(x)=emx+x2-mx.

(I)证明：f(x)在(-∞,0)单调递减，在(0,+∞)单调递增；

(II)若对于任意x1,x2∈[-1,1]，都有|f(x1)-f(x2)|≤e-1，求m的取值范围.

解析(I)f′(x)=m(emx -1)+2x.若m≥0，则当x ∈(-∞,0)时，emx-1 ≤0，f′(x)＜0；当x ∈(0,+∞)时，emx -1 ≥0，f′(x)＞0.若m＜0，则当x ∈(-∞,0)时，emx -1＞0，f′(x)＜0； 当x ∈(0,+∞)时，emx -1＜0，f′(x)＞0.所以f(x)在(-∞,0)单调递减，在(0,+∞)单调递增.

(II)由(I)知，对任意的m，f(x)在[-1,0]单调递减，在[0,1]单调递增，故f(x)在x=0 处取得最小值，所以对于任意x1,x2∈[-1,1]，都有|f(x1)-f(x2)|≤e-1 的充要条件是：令g(t)=et-t-e+1，则g′(t)=et-1，当t＜0 时，g′(t)＜0；当t＞0 时，g′(t)＞0.故g(x)在(-∞,0)单调递减，在(0,+∞)单调递增.又g(1)=0，g(-1)=e-1+2-e＜0，故当t ∈[-1,1]时，g(t)≤0，当m ∈[-1,1]时，g(m)≤0，g(-m)≤0，当m＞1 时，根据g(t)单调性，g(m)＞0； 当m＜-1 时，g(-m)＞0，综上m的取值范围是[-1,1].

题型六：导数与不等式证明

函数与不等式的证明在高考中主要出现在第21 题第二问的位置，难度较大，详情如下：

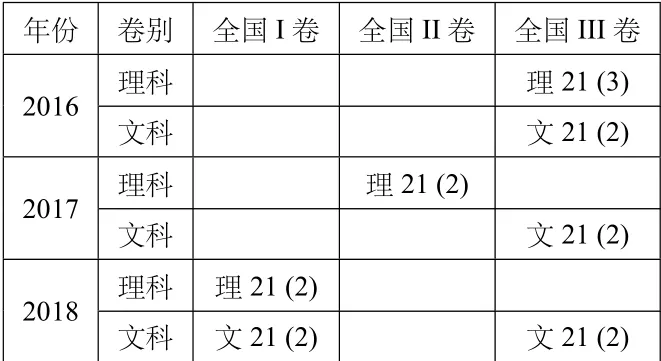
表8：2016—2018年导数与不等式证明在全国卷的考查情况

1.解题方法：利用等价转化的思想，将函数不等式的证明转化为最值问题.

2.解题思路：(1)构造函数f(x)；(2)求f(x)的导函数f′(x)；(3)研究函数的单调性；(4)求最值；(5)下结论.

例6(2018 全国I 卷理科第21 题)已知函数f(x)=

(I)讨论f(x)的单调性；

(II)若f(x)存在两个极值点x1,x2，证明：

解析(I)由题意知，f(x)的定义域为(0,+∞)，且

(i)若a≤2，则f′(x)≤0，当且仅当a=2,x=1 时，f′(x)=0，所以f(x)在(0,+∞)单调递减.

(ii)若a＞2，令f′(x)=0，得：x1=或当时，f′(x)＜0；当x∈时，f′(x)＞0.所以f(x)在单调递减，在单调递增.

(II)解法1由(I)知，f(x)存在两个极值点当且仅当a＞2.所以f(x)的两个极值点x1,x2满足x2-ax+1=0，所以x1x2=1.不妨设x1＜x2，则x2＞1.由于

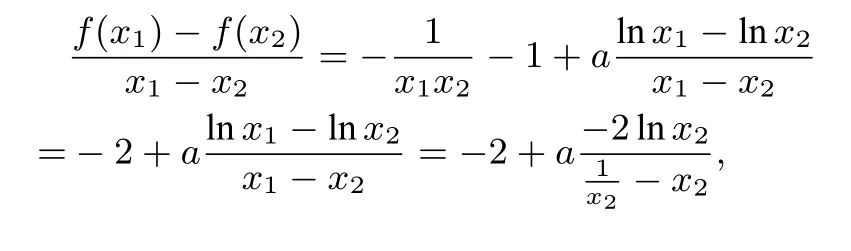
解法2由(I)知，f(x)存在两个极值点当且仅当a＞2.所以f(x)的两个极值点x1,x2满足x2-ax+1=0，所以x1x2=1.不 妨 设x1＜x2，则0＜x1＜1.要证只 需证：即 证：即1，由x2=只需证即证：2 lnx1＞x1-即证：2xlnx - x2+1＞0，0＜x＜1.设h(x)=2xlnx - x2+1，0＜x＜1，h′(x)=2 lnx+2-2x=2(lnx+1-x)，h′′(x)=即h′(x)＜h′(1)=0，0＜x＜1.于是h(x)在(0,1)上单调递减，从而，h(x)＞h(1)=0，故

解法3由(I)知，f(x)存在两个极值点当且仅当a＞2.所以f(x)的两个极值点x1,x2满足x2-ax+1=0，所以x1x2=1.要证：a -2，即证：因为a＞2，所以，只需证：设x1＞x2，由(I)知：即证：令h(a)=2 ln所以，h(a)在(2,+∞)上单调递减.故h(a)＜h(2)=0，故

函数与导数部分是高考命题的重点和热点，并且难度大、综合性强，对学生的数学核心素养提出了较高的要求.本文整理和分析近三年全国卷的考点，便于广大师生了解高考命题规律，同时，经过近三年全国卷试题关于函数与导数部分的梳理，将试题划分为6 个常见类型问题，对每种题型配合经典例题进行方法总结，为高三二轮复习提供方向和建议.