也谈高考中的函数零点问题

广东省佛山市第一中学(528000) 吴统胜

函数的零点问题是新课标增加的考查内容，这种问题往往具有知识点多、覆盖面积广、综合性强的特点，是集数形结合、转化与化归、函数与方程、分类讨论四大数学思想方法于一身的良好题材，能有效考查学生的思维水平和解题能力.随着高考对导数知识考查的深入，进一步拓宽了对函数零点问题的命题空间和解题空间，以致在近几年来的高考或模拟考中，试题的难度、深度和广度都在不断加大，试题的背景、结构、交汇更加丰富、更加活泼、更加新颖.函数零点问题已悄然成为逐步升级的高考亮点和高考热点.本文笔者将通过对高考题或高考模拟题中函数零点问题的解法及处理策略的研究与探讨，总结归纳了函数零点问题的一般性解题策略和方法，以期对广大师生在解决此类问题时带来一定的帮助.

一.函数零点与不等式证明的综合问题

例1[1]已知x1,x2是函数f(x)=ex-ax的两个零点，且x1＜x2，求证：x1x2＜1，x1+x2＞2.

点评本题考查了导数在研究函数中的综合运用，涉及了函数零点及不等式证明问题，解答的关键在于利用消元思想，先消去参数，转化为含双变量x1,x2的不等式，再利用“二元化一元”的思想，通过等价换元再构造函数得证，常需利用到高等数学中的洛必达法则.x1+x2＞2 的证明也可利用函数极值点偏移问题的一般处理策略.详细解答请参见[1].

例2[1],[4](2016年全国卷I 理科第21 题)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(I)求a的取值范围；

(II)设x1,x2是f(x)的两个零点，证明：x1+x2＜2.

点评本题考查函数零点概念以及导数公式和导数运算法则，考查学生灵活运用导数工具分析问题、解决问题的能力，综合考查考生的逻辑推理能力、运算求解能力、推理论证能力以及转化与化归、分类讨论、数形结合的思想.详细解答参见[1]及[4].

第(II)问要求证明的两个零点满足x1+x2＜2，将函数与不等式有机结合，试题设置不能直接求出零点，证法一需要考生打破常规思路，将x1+x2＜2 转化为f(x1)＞f(2-x2)，进而通过构造辅助函数g(x)=f(2-x)，研究辅助函数g(x)的单调性得到问题的证明! 此问对考生运用所学知识寻找合理的解题策略以及推理论证能力都提出了较高要求，突出选拔功能! 证法二利用函数极值点偏移问题的处理策略，是程序化解法.目前，极值点偏移问题的流行解法与2010年天津市高考题的命题结构具有高度的近似性，形成了程序化思路.当导函数结构比较复杂、难于求出导函数零点时，可以通过二阶求导、对解析式的局部求导、调整解析式结构后再求导来解决极值问题.该题第(II)问题干设置与解法同2010年天津20 题第(3)问，其题目如下：

(2010年天津理)已知函数f(x)=xe-x(x ∈R).

(1)求函数f(x)的单调区间和极值；

(2)已知函数y=g(x)的图像与函数y=f(x)的图像关于直线x=1 对称.证明：当x＞1 时，f(x)＞g(x)；

(3)如果x12且f(x1)=f(x2)，证明：x1+x2＞2.

二.不等式证明中的隐性零点问题

例3[1]-[4](2013年课标II 理科第21 题)已知函数f(x)=ex-ln(x+m).

(1)设x=0 是f(x)的极值点，求m，并讨论f(x)的单调性；

(2)当m≤2 时，证明：f(x)＞0.

详细解答请参见[1]或[4].

点评证法一优先消去参m，转化为求函数的最小值问题，思路虽简单，但由于最小值φ(x0)对应的x0不可求，涉及函数隐性零点问题，需利用函数零点存在定理及设而不求法较巧妙地解决了该证明问题，对思维及转化能力的要求相当高.证法二利用函数型不等式：ex≥x+1(x ∈R)及ln(x+1)≤x(x＞-1)进行放缩证明，证明过程相当快捷、简便.证法三利用“公切线”法证明，体现了数形结合思想，方法相当精妙，可实现精准放缩，证明方向也相当明确.但此方法只适用于一凸、一凹函数类型，若两函数同为凸函数或凹函数，可对不等式作适当变形，转化为一凸、一凹函数类型，再用“公切线”法证明.通过一题多解的例题讲解，可以培养学生思维的发散性与深刻性，感悟数学本质，提升数学核心素养.

方法的优化、拓展、一般化

下面把证法二、三的方法优化、整合拓展一下，常见的函数y=ex，y=lnx，y=xlnx(x＞0)我们均可以把它们放缩为如下一次函数形式(可利用构造函数法证明)：

函数型不等式1ex≥kx+k-klnk(k＞0).

函数型不等式2lnx≤kx-lnk-1(x＞0，k＞0)，该不等式可变式为：lnx≤e-(m+1)x+m(x＞0，m ∈R).

函数型不等式3xlnx≥kx-ek-1(x＞0，k ∈R).

三.函数零点与不等式恒成立条件下的参数取值范围问题

例4(2010 海南、宁夏文第21 题)设函数f(x)=x(ex-1)-ax2.

(1)略；(2)若当x≥0 时，f(x)≥0.求a的取值范围.

解析当x≥0 时，f(x)≥0⇔g(x)=ex-1-ax≥0.当x=0 时，g(x)≥0 恒成立，此时a ∈R.当x＞0时，g(x)≥0⇔a≤设设h(x)=xex -ex+1(x＞0)，因为h′(x)=xex＞0，所以h(x)在(0,+∞)上递增，所以h(x)＞h(0)=0，所以φ′(x)＞0，所以φ(x)在(0,+∞)上递增，所以φ(x)＞φ(0)，但φ(0)无意义.

解法一因为由高等数学中的洛必达法则有所以

解法二联想到导数的概念得所以a的取值范围为(-∞,1].

点评本题分离参数后多次构造函数或局部函数求导，最后遇到了一个“不定型”函数极限问题.如何突破该解题障碍? 解法一利用高等数学中的洛必达法则，轻松破解了该压轴题，但由于涉及高等数学知识，普通学生不易理解掌握；解法二结合函数式的结构特征，联想到导数的概念，非常巧妙地破解了该压轴题.数学概念是数学应用的“根”和“本”，根深才能长成参天大树，本固才能立于不败之地.

例5(2017 全国II 文科第21 题)设函数f(x)=(1-x2)ex.

(1)略；(2)当x≥0 时，f(x)≤ax+1，求a的取值范围.

解析当x≥0时，f(x)≤ax+1⇔a≥设函数所以设函数h(x)=1-(x3+x2-x+1)ex，因为h′(x)=-(x3+4x2+x)ex＜0，所以h(x)在(0,+∞)上递减，所以h(x)＞h(0)=0，所以φ′(x)＞0，所以φ(x)在(0,+∞)上递增，但φ(0)不存在，联想到导数概念有1，所以a≥1，所以a的取值范围为[1,+∞).

例6(2015年武汉模拟)设函数f(x)=1-x2+ln(x+1).

(1)求函数f(x)的单调区间；

(2)若不等式f(x)＞-x2(k ∈N∗)在(0,+∞)上恒成立，求k的最大值.

解(1)略；(2)解法一直接分离参数

解法二线性分离方式

由题意，1+ln(x+1)＞在(0,+∞)上恒成立.设g(x)=1+ln(x+1)-(x＞0)，则g′(x)=

(1)当k=1 时，则g′(x)=所以g(x)单调递增，g(0)=1＞0，即g(0)＞0 恒成立.

(2)当k＞1 时，则g(x)在(0,k -1)上单调递减，在(k-1,+∞)上单调递增，所以g(x)的最小值为g(k-1)，只需g(k-1)＞0 即可，即lnk-k+2＞0.设h(k)=lnk-k+2则h(k)单调递减，因为h(2)=ln 2，h(3)=ln 3-1＞0，h(4)=ln 4-2＜0，所以k的最大值为3.

四.求函数零点个数问题

例7已知函数f(x)=klnx-x2，k ∈R.

(1)若f(x)在(0,1]上是增函数，求k的取值范围；

(2)讨论函数f(x)的零点个数.

解析(1)略； (2)恰当分离参数，数形结合，常需分类讨论.

当k=0 时，f(x)=-x2(x＞0)没有零点.当k0 时方程f(x)=设g(x)=(x＞0)，则g′(x)则有而x→0 且x＞0，g(x)→-∞；x→+∞且x＞0，g(x)→0 且g(x)＞0.

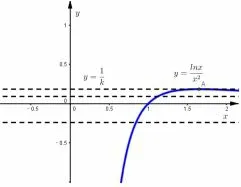
图1