由一个向量题谈三角形四心的向量表示

江苏省启东市汇龙中学(226200) 朱玉华

题目若O是三角形ABC内一点(如 图1)，则

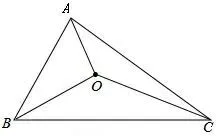
图1

图2

引理1若O是三角形ABC内一点，且S△OBC=S△OAC=S△OAB，则O是三角形ABC的重心.

证明延长AO交BC于D，延长BO交AC于E，延长CO交AB于F，连接EF，如图2．因为△ABD与△ACD同高，所以S△ABD:S△ACD=BD:CD，同理S△OBD:S△OCD=BD:CD，利用分比性质，得(S△ABD -S△OBD):(S△ACD -S△OCD)=BD:CD，即S△AOB:S△AOC=BD:CD，因为S△OAB=S△OBC=S△OAC，所以BD=CD，所以点D是BC的中点，同理E、F分别是AC、AB的中点，所以O是三角形ABC的重心.

引理2在三角形ABC中，点G是△ABC重心的充要条件是

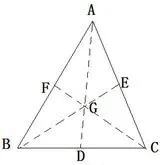
图3.7

证明(必要性)如图3，设BC、CA、AB的中点分别为D、E、F，连接AD、BE、CF，则AD、BE、CF相交于重心G，所以又D是BC的中点，所以因为所以所以所以

综上，引理得证.

题目证明如下：

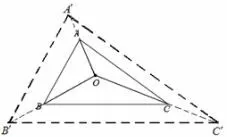
图4

证明令连A′B′，B′C′，C′A′(如图4)则S△OABS△OBCS△OAC，同理，S△OB′C′=S△OABS△OBCS△OAC，S△OA′C′=S△OABS△OBCS△OAC，所以S△OA′B′=S△OA′C′=S△OB′C′，所以O是三角形A′B′C′的重心.所以即

特别地，

结论1若O是三角形ABC的重心，则

因为 当O是三角形ABC的重心时，S△OBC=S△OAC=S△OAB，所以

结论2若O是三角形ABC内心，则即

因为 当O是三角形ABC内心时，(其中r是三角形ABC内切圆的半径).所以即由正弦定理得sinA-→OA+

结论3若O是三角形ABC内一点，且O是三角形ABC外心，则

因为当O是三角形ABC外心时，OC·sin ∠BOC，S△OAC=·OA·OC·sin ∠AOC，S△OAB=·OA·OB·sin ∠AOB，所以即

结论4若O是三角形ABC内一点，且O是三角形ABC垂心，则

图5

因为当O是三角形ABC垂心时，延长AO交BC于D，延长BO交AC于E，延长CO交AB于F(如图5)，OD·tanB，所以同理，所以S△OBC:S△OAC:S△OAB=tanA:tanB:tanC，即∃λ＞0，使得S△OBC=λtanA，S△OAC=λtanB，S△OAB=λtanC，所以