数学解题要重视挖掘“特征”

山东省泰安英雄山中学(271000) 尹承利

许多数学问题中，无论是条件、结论，还是数值、结构形式等等，都常常表现出或暗含着某些“特征”，这些“特征”是问题的“题眼”，是解决问题的切入点.解题时，要重视挖掘这些“特征”，并由此进行分析、变换、联想、构造，这样可以快速获得解决问题的途径或优化问题解决的过程.下面从几方面阐述挖掘“特征”在数学解题中的应用.

1.“数值”特征

许多数学问题，都会出现具有某种特征的数值[1]，会对问题的解决起着导向作用.只要注意观察、分析，重视挖掘，从数值本身的变化、数值与数值之间的联系去寻找解题的切入点.

例1已知sinθ·cosθ=且求sinθ,cosθ的值.

解析数字暗含了特征也暗含着由此得解.

因为sinθ·cosθ=且1，由所以sinθ＞cosθ.故得

点评本题若按常规方法，由已知sinθ·与sin2θ+cos2θ=1 联立，求出sinθ,cosθ，计算量较大.这里注意到数值特征，简捷获解.

例2已知正实数a,b满足2a+b=1，则的最小值是____.

解析条件式2a+b=1，而目标分式第二项的分母中有“1”，这就暗示我们首先去进行“1”的代换.当且仅当即时，等号成立.故的最小值是

点评“1”的代换后就将分式化为了齐次式，进而或通分并分离常数，或换元转化，变形出基本不等式的应用形式求解.数值“1”起了关键性的作用.

2.“位置”特征

与图形(象)有关的一些数学问题都有它特定的位置关系，若能细致分析某些关键的点或线的位置“特征”，不仅可以简化运算过程，甚至可以得到不攻自破的解题效果.

例3(2018 高考全国卷III)直线x+y+2=0 分别与x轴，y轴交于A,B两点，点P在圆(x-2)2+y2=2 上，则△ABP面积的取值范围是( )

A.[2,6]B.[4,8]C.D.

解析由于|AB|是确定的，所以△ABP面积的取值范围取决于点P到直线x+y+2=0 的距离.所以过圆心作直线x+y+2=0 的垂线，与圆的交点即为所求的点P的位置.因为直线x+y+2=0 分别与x轴、y轴相交于A、B两点，所以A(-2,0)，B(0,-2)，设圆(x -2)2+y2=2 的圆心到直线x+y+2=0 的距离为d′，则于是，圆(x-2)2+y2=2 上的点到直线x+y+2=0的距离的最小值为最大值为圆的半径)，于是，圆上的点到直线的距离d的取值范围为得 到故选A.

点评这里若不能发现“过圆心作直线x+y+2=0 的垂线，与圆的交点即为所求的点P的位置”是顺利解决问题的关键.

例4对于函数f(x)满足：当x ∈(-∞,+∞)时，f(2- x)=f(2+x)且f(7- x)=f(7+x)，在闭区间[0,7]上f(x)只有两个零点：x1=1,x2=3.

(I)试判断函数f(x)的奇偶性；

(II)试求方程f(x)=0 在闭区间[-2020,2020]上的根的个数，并证明你的结论.

解析由条件无法求出f(x)的解析式，所以不能直接解方程f(x)=0 来求根的个数.若通过对问题中隐含的图象位置特征进行分析，即由f(2-x)=f(2+x)知函数f(x)的图象关于直线x=2 对称，同样由f(7-x)=f(7+x)知关于直线x=7 对称.这样函数f(x)的图象有两条对称轴，根据经验，函数f(x)一定是周期函数.

从周期出发，我们可以思考两点：(I)借助f(1)=f(3)=0 可以求出一些函数值，由此可以发现奇偶性； (II)求出一个周期上方程f(x)=0 根的个数，再由周期性得出在区间[-2020,2020]上的所有根的个数.由f(4-x)=f(14-x)⇒f(x)=f(10+x)，即函数f(x)是以10 为周期的周期函数.

(I)由于在闭区间[0,7]上只有f(1)=f(3)=0，所以f(-3)=f(7)0，显然f(-3)(3)且f(-3)(3)，则f(x)是非奇非偶函数.

(II)由f(1)=f(3)=0 得f(11)=f(13)=f(-9)=f(-7)=0，可知f(x)=0 在区间[0,10]及[-10,0]上各有两个根，因此，f(x)=0 在区间[0,2020]上有403 个根，在区间[-2020,0]上有403 个根.故在[-2020,2020]上的所有根的个数为806 个.

点评本题从函数图象的位置特征中寻找到函数的周期规律，是迅速解决问题的关键.

3.“图形”特征

有些抽象的数量关系，若转化为具体的图形问题，并抓住图形特征，则思路直观、清晰，有利于快速解题.

例5(2017年高考全国卷I )已知向量a,b的夹角为60°，|a|=2，|b|=1，则|a+2b|=____.

解析利用如下图形，可以判断出a+2b的模长是以2 为边长的菱形对角线的长度，则为

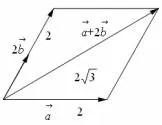
图1

点评向量具备代数和几何特征，在处理涉及向量模的一类问题时，若充分运用“图形特征”会加快解题速度，可使问题得以“秒杀”.

例6若直线y=x+b与曲线有公共点，则b的取值范围是( )

图2

解析如图2，在平面直角坐标系内画出曲线y=3-与直线y=x，在平面直角坐标系内平移该直线，结合图形分析可知，当直线沿左上方平移到过点(0,3)的过程中的任何位置相应的直线与曲线y=3-都有公共点；当直线沿右下方平移到与以点C(2,3)为圆心、2 为半径的圆相切的过程中的任何位置相应的直线与曲线都有公共点.注意与y=x平行且过点(0,3)的直线方程是y=x+3；当直线y=x+b与以点C(2,3)为圆心、2 为半径的圆相切时，有结合图形可知，满足题意的b的取值范围是故选D.

点评本题若不运用“图形”，而是去联立方程，用代数的方法求解，几乎是不可能完成的.

4.“结构”特征

数学问题条件或结论中的数、式结构常常隐含着某种特殊的关系，注意洞察并加以分析、加工和转化，可迅速找到问题解决的思路.

例7(2016年高考四川卷)△ABC的内角A,B,C的对边分别是a,b,c，且

(I)证明：sinAsinB=sinC；

解析(I)略.(II)式子b2+c2- a2=呈现的是边的平方与积的结构形式，由此我们可联想到余弦定理.由b2+c2- a2=根据余弦定理可知，cosA=因为A为三角形内角，A ∈(0,π)，sinA＞0，则sinA=即由(I)可知所以所以tanB=4.

点评本题将条件中给出的边长a,b,c的关系”式，变形利用余弦定理求出cosA后进而利用同角的平方关系和商数关系求解的.从b2+c2-a2=的结构联想到余弦定理是解题的关键.

例8已知函数y=f(x)定义在R 上，其图象关于坐标原点对称，且当x ∈(-∞,0)时，不等式f(x)+xf′(x)＜0 恒成立，若a=20.2f(20.2)，b=ln 2f(ln 2)，则a,b,c的大小关系是( )

A.a＞b＞cB.c＞b＞a

C.c＞a＞bD.a＞c＞b

解析观察不等式f(x)+xf′(x)＜0 左边的结构，我们联想积的导数运算法则，逆用法则构造函数求解.构造函数g(x)=xf(x)，则g′(x)=[xf(x)]′＜0.当x ∈(-∞,0)时，g′(x)＜0，故函数y=g(x)在(-∞,0)上单调递减.由于函数y=f(x)的图象关于坐标原点对称，所以y=f(x)是奇函数，故函数y=g(x)是偶函数，根据偶函数的性质，函数y=g(x)在(0,+∞)上单调递增，又a=g(20.2)，b=g(ln 2)，c=g(-2)=g(2).由于0＜ln 2＜lne=1，根据指数函数的性质1=20＜20.2＜21=2，所以ln 2＜20.2＜2，故c＞b＞a.故选C.

点评本题通过条件中不等式的结构，逆用了导数运算的乘法法则后构造函数，综合利用函数的单调性、奇偶性及指、对、幂运算和函数的性质解答的.

5.“差异”特征

许多数学问题的条件与结论之间、“量”与“量”之间，往往表现出一些“差异”关系，这些“差异”以特有的方式直接或间接地暗示着解题的方向.

例9已知函数f(x)=

(I)若函数y=f(x)的定义域为R，求实数a的取值范围；

(II)在(I)的条件下，若对于∀x1∈R，∃x2∈(-∞,-1]，使得f(x1)＞g(x2)，求实数a的取值范围.

解析(I)实数a的取值范围为(2,+∞).(II)x1是任意量，x2是存在量，从这一“差异”中我们可以意识到问题需要转化求解才能奏效.对于∀x1∈R，∃x2∈(-∞,-1]，使得f(x1)＞g(x2)，等价于对于∀x1∈R，∃x2∈(-∞,-1]，f(x)min＞g(x)min.

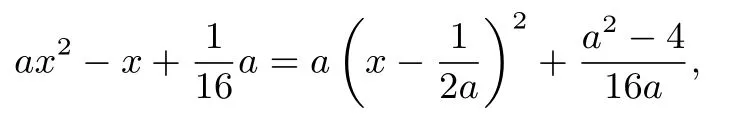
因为a＞2，所以函数

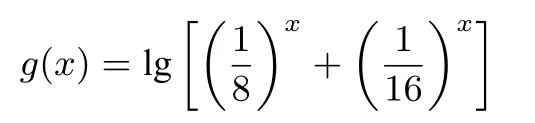
在(-∞,-1]上单调递减，所以

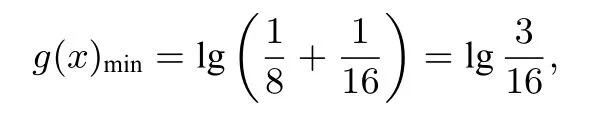
由

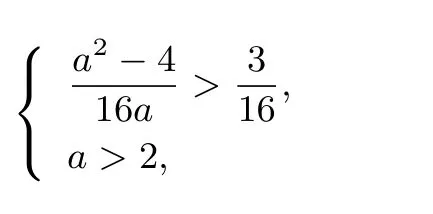
解得a＞4.所以实数a的取值范围为(4,+∞).

点评数学中的“任意量”与“存在量”常见常用，变式多样，丰富多彩，内涵深刻[2].本题依据“量”与“量”之间的差异，将条件不等式的成立等价转化为函数的最值关系求解，体现了化归转化思想的应用.

例10设等差数列{an}的各项与公差均为正数，Sn是其前n项的和；Tn是数列{a2n}的前n项和.若对于一切正自然数n，Sn≤n2+n-1，Tn≥试求{an}的首项a1和公差d.

解析条件中给出了两个“不等量”关系，结论探求的是“等量”关系.通过对这一差异“点”的分析，获知解题的切入点就是化“不等”为“等”.因为Sn≤n2+n-1，所以S1=a1≤12+1-1=1，即

由①、②得a1=1.又因为Sn≤n2+n -1，即所以对一切正自然数n恒成立，故

因为Tn=a21+a22+a23+···+a2n=a21+(a1+d)2+(a1+2d)2+···+[a1+(n-1)d]2=na21+2[1+2+3+···+(n-1)]a1d+[12+22+32+···+(n-1)2]d2=na21+n(n-所以由得所以(2n-1)d2+6d-8(n+1)≥0，所以0.又所以d-2 ≥0，即

故由③、④可得d=2.

点评本题通过对“等”与“不等”的差异“点”的分析转化，使得不等式中的“夹逼”法则：“如果实数x、a满足a≤x≤a(即x≥a且x≤a)，则必有x=a”在求解本题中起了重要的作用.