解析几何模块第二轮复习备考建议

华中师范大学第一附属中学(430223) 王雪冰

华南师范大学数学科学学院(510630) 林晓珊

一、2016-2018年全国卷I 卷试题考点分析

为了更好的把握考点，突破重点，笔者将近3年全国文理I 卷中解析几何考点做了整理，以求更好地探索出命题规律，提高高考二轮复习的针对性，整理如下表一、表二.

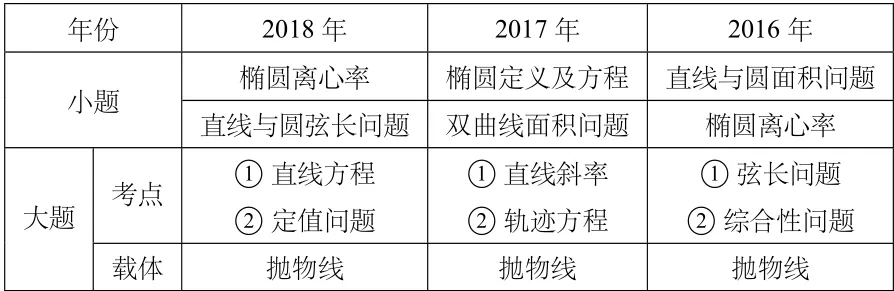
表二：2016-2018年全国卷I 解析几何文科考点统计表

由表一、二可知近3年全国I 卷中解析几何的考查特点：

(1)题量稳定，分值稳定.2016-2018年全国高考文理I 卷严格遵循考纲要求，考查题量一般为三道题，均为两道小题一道大题，分值稳定，均为22 分.

(2)知识考查以基础为主，稳中有升.在宏观知识的考查范围上，圆、椭圆、双曲线、抛物线均有涉及，其中双曲线的考查以客观题为主，椭圆与抛物线较多作为解答题的载体.

在客观题的考查上，理科主要以双曲线、抛物线为主，文科主要以椭圆、圆与直线为主.考查内容主要是圆锥曲线、直线与圆的定义、几何性质及基本量求解.难度则是基础与中等相结合，题型新颖，位置不定.

在解答题中，理科主要以椭圆为载体，文科主要以抛物线为载体，来考查定点、定值问题，弦长问题，面积问题，范围问题、探索性问题等，其中定点、定值问题是近年高考理科解答题的考查热点.解答题题目设问层层递进，第一问难度较缓，均为考查基本知识点，第二问有一定的难度梯度，主要考查学生逻辑推理能力、分析与计算能力.解答题一般作为倒数第二道压轴题目，着重考查学生对知识的综合应用能力.

(3)解法多种，趋向于多想精算.高考数学注重对学生基本概念和思想的考查，而解析几何则更注重“代数”与“几何”相结合.如果许多题目仅通过代数解决问题会相对繁琐，但从“几何角度”入手可以更为简便地剖析出问题本质，再辅以计算，则既可精简计算量，又可逐步培养学生逻辑推理分析能力.

二、常见考题类型

为了使高考二轮复习更加有针对性，笔者通过整理近3年全国文理卷的相同考点分布情况，总结出六种常考题型，希望能够给读者提供一定的启示.

题型一：考查曲线定义及标准方程问题

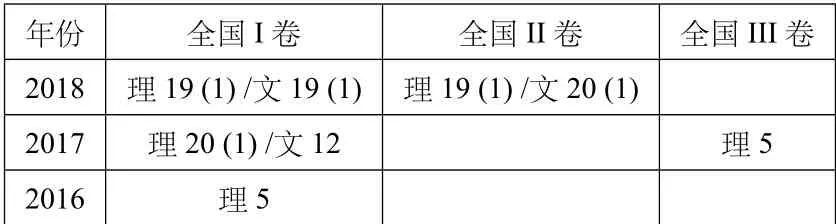
表三：2016-2018年全国文、理科卷曲线定义及标准方程考查统计表

由表三可以发现全国卷对于曲线定义及标准方程的考查较为简单，均只考查简单定义，故只要学生牢牢掌握住曲线定义即可解决问题.

例1(2017年高考全国卷I 文科)设A,B是椭圆长轴的两个端点，若C上存在点M满足∠AMB=120°，则m的取值范围是( )

A.(0,1]∪[9,+∞) B.

C.(0,1]∪[4,+∞) D.

解析①当0＜m＜3 时，焦点在x轴上，要使C上存在点M满足∠AMB=120°，则即得0＜m≤1； ②当m＞3 时，焦 点在y轴上，要使C上存在点M满足∠AMB=120°，则即得m≥9，故m的取值范围为(0,1]∪[9,+∞)，选A.

总结基于圆锥曲线的定义，求解其标准方程基本的步骤是：先定形，再定量.在本题中，学生只有牢牢抓住问题本质，才能领悟需要分类讨论的原因.由此体现出巩固基础知识十分重要.

对于一般求标准方程问题考查的几种基本解法为：

①直接求，圆锥曲线的一般方程多考虑用待定系数法来确定方程的基本量(如a,b,c,e)，进而确定曲线方程(2017年高考全国卷III 理科第5 题)；

②若所求为双曲线方程且已知渐近线，则可利用设公共渐近线的双曲线为来求解(如2015年新课标II 文科卷第15 题).

题型二：考查椭圆、双曲线几何性质(以离心率、渐近线为主)

表四：2016-2018年高考全国卷离心率与渐近线考查统计表

由表四可以发现，解析几何对于几何性质的考查相对全面，建议教师在复习过程中不仅要引导学生学会用一般的代数方法解决，也要引导其学会从简单的几何性质入手辅助计算来快速解决问题.

常见几种考查曲线几何性质的类型：

①若图形中出现三角形，可多考虑正、余弦公式(如2018年高考全国卷III 理科第12 题)，正、余弦定理(如2018年高考全国卷II 理科第11 题)，全等、相似三角形(如2016年高考全国卷|lm3 理科第11 题)等.

②若图形为圆锥曲线与直线相结合，则需多考虑点到直线距离公式(如2017年高考全国III 理科第10 题)，两点之间距离公式，正、余弦公式，向量基本定理等.

同时在解题过程中辅助以二级推论(如双曲线焦点到渐近线距离为定值，椭圆、双曲线焦半径为定值等)，同时结合曲线基本定义与几何性质则可以更为便捷解决问题.

例2(2016年高考全国卷III 理科)已知O为坐标原点，F是椭圆的左焦点，A,B分别为C的左，右顶点.P为C上一点，且PF⊥x轴.过点A的直线l与线段PF交于点M，与y轴交于点E.若直线BM经过OE的中点，则C的离心率为( )

解析

解法1(代数角度)由题可知F(-c,0)，A(-a,0)，设BM与y轴交点为G.设直线l为y=k(x+a)(k＞0)①，可得E(0,ak)，由题可知PF:x=-c②，联立① ②可得M(-c,k(a - c))，所以直线BM斜率为故BM为解得由题可知直线BM经过OE中点，故解得a=3c，所以椭圆C的离心率为

解法2(几何角度)由题意设直线l的方程为y=k(x+a)，分别令x=-c与x=0 得|FM|=|k|(a-c)，|OE|=|k|a.设OE的中点为N，则△OBN～△FBM，则即整理，得所以椭圆C的离心率为故选A.

总结由例2 两种解法可知，几何角度比代数角度更为快捷直接，这反映了高考对学生的要求不仅仅是模式化的计算能力，更是要求学生具有逻辑思维能力与分析能力.培养学生从几何角度分析问题不仅可以简化计算量，而且可以更好的培养学生数学思维与能力.同时也可发现，让学生记忆一些二级推论有助其更迅速地联想到几何性质，同时加快解题速度.

题型三：考查抛物线几何性质(以准线为主)问题

表五：2016-2018年全国文、理科卷抛物线几何性质问题考查统计表

抛物线的准线是抛物线一个十分重要的几何性质，它可以将抛物线上的点到焦点的距离与到准线的距离进行相互转化，促进问题简单化.

例3(2017年高考全国卷II 理科)已知F是抛物线C:y2=8x的焦点，M是C上一点，FM的延长线交y轴于点N.若M为FN的中点，则|FN|=____.

解析如图所示，不妨设点M位于第一象限，设抛物线的准线l与x轴交于点F′，作MB⊥l于点B，NA⊥l于点A，由抛物线的解析式可得准线方程为x=-2，则|AN|=2，|FF′|=4，在直角梯形ANFF′中，中位线由抛物线的定义有：|MF|=|MB|=3，结合题意，有|MN|=|MF|=3，故|FN|=|FM|+|MN|=3+3=6.

图1

题型四：考查(轨迹)方程问题

表六：2016-2018年全国文、理科卷(轨迹)方程问题考查统计表

运动轨迹所给出来的条件千差万别，因此求轨迹方程的方法也是多种多样，常用的几种方法主要有：待定系数法、直译法、相关点法、参数法.

①待定系数法：从题目中已知曲线的定义(如椭圆、双曲线等)，通过条件确定已知常量，即得出轨迹方程(如2018年高考全国卷II 理科第19 题)；

②直译法：求轨迹方程最常用的方法，通过题目条件代入满足几何的等量数量关系，求出其结果.

③相关点法：动点P的轨迹是与另一动点相关的，建立两者之间的等量关系即可求出结果(如2017年高考全国卷III 理科第20 题).

例4(2016年高考全国卷III 理科)已知抛物线C:y2=2x的焦点为F，平行于x轴的两条直线l1,l2分别交C于A,B两点，交C的准线于P,Q两点.

(2)若△PQF的面积是△ABF的面积的两倍，求AB中点的轨迹方程.

解析由题设设l1:y=a，l2:y=b，则ab0，设R为PQ中点，记过A,B两点的直线为l，则l的方程为2x-(a+b)y+ab=0.

(2)设l与x轴的交点为D(x1,0)，则由题设可得所 以x1=0 (舍去)，x1=1.设满足条件的AB的中点为E(x,y).当AB与x轴不垂直时，由kAB=kDE可得而所以y2=x-1(x1).当AB与x轴垂直时，E与D重合.所以，所求轨迹方程为y2=x-1.

例5(2018年高考全国卷II 理科)设抛物线C:y2=4x的焦点为F，过F且斜率为k(k＞0)的直线l与C交于A,B两点，|AB|=8.

(1)求直线l的方程；

(2)求过点A,B且与C的准线相切的圆的方程.

解析(1)l的方程为y=x-1(过程略).

(2)解法一(纯代数角度)由(1)得AB的中点坐标为(3,2)，所以AB的垂直平分线方程为y-2=-(x-3)，即y=-x+5.设所求圆的圆心坐标为(x0,y0)，则半径为x0+1，圆心到AB的距离为又因为圆心在直线y=-x+5，所以可得解得或因此所求圆的方程为(x-3)2+(y-2)2=16 或(x-11)2+(y+6)2=144.

解法二(几何、代数角度相结合)由抛物线的二级推论可知，以直线AB的中点M为圆心，以AB长度为半径的圆与抛物线的准线相切.故半径为4，可求得(x-3)2+(y-2)2=16.另一解法则可由r=|MA|解得.

总结 例4 采用的是直译法，通过题目的已知三角形面积建立等价的数量关系，从而得出轨迹方程.例5 则是采用待定系数法，已知所求为圆的方程，通过圆的几何性质求出圆点与半径.因此求曲线的轨迹方程要学会“执果”并采取适当方法入手“索因”，以此更高效地解决问题.

题型五：考查曲线的定点、定值问题

定点、定值问题是近几年高考理科大题的热点，从表七可以得知，近两年的全国I、II 卷考查频率较高，题目相对来说较为灵活，需要学生从“变”中寻找“不变”，牢牢抓住问题变化的关键.

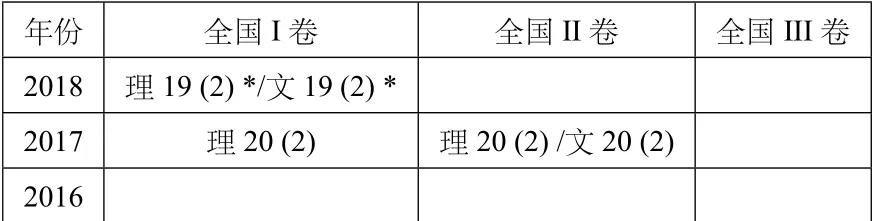
表七：2016-2018年全国文、理科卷曲线定点、定值问题考查统计表

化解定点这类问题的关键就是引进变的参数表示直线方程、数量积、比例关系等.根据等式的恒成立、数式变换等寻找不受参数影响的量.

解决直线过定点问题通法：设出直线方程，通过已知条件找出一次函数关系式，代入直线方程即可.

圆锥曲线定点问题的几种常用解法：

①“手电筒”模型：过圆锥曲线上某一点P的直线与曲线交于A,B两点，只要任意一个限定条件(如kAP ·kBP=定值，kAP+kBP=定值，P为某特殊点等)直线AB会过某定点(如例5).

②切点弦恒过定点(如2017年高考全国卷II 理科第20 题)；

③相交弦恒过定点；

例6(定点问题)(2017年高考全国卷I 理科)已知椭圆四点P1(1,1)，P2(0,1)，中恰有三点在椭圆C上.

(2)设直线l不经过点P2且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为-1，证明：l过定点.

解析(1)过程略.C的方程为(2)设直线P2A与直线P2B的斜率分别为k1,k2，如果l与x轴 垂 直，设l:x=t，由题设知且|t|＜2，可得A,B的坐标分别为则得t=2，不符合题设.从而可设l:y=kx+m(m1).将y=kx+m代入得，(4k2+1)x2+8kmx+4m2-4=0，即由题设可知Δ=16(4k2-m2+1)＞0.设A(x1,y1)，B(x2,y2)，则而由 题 设k1+k2=-1，故(2k+1)x1x2+(m-1)(x1+x2)=0，即(2k+1)·解 得又因为4k2- m2+1＞0，可得m＞-1.当且仅当m＞-1时，Δ＞0，所以l 的方程为：即所以l过定点(2,-1).

圆锥曲线定值问题的几种常用解法：

(1)特殊探路，一般论证.(从特殊入手，求出其值，再证明这个值与变量无关.这符合一般到特殊的思维辩证关系)

(2)直接推理、计算.在计算推理的过程中消去变量，从而得到定值(如例7).

例7(定值问题)(2018年高考全国卷I 理科)设椭圆的右焦点为F，过F的直线l与C交于A,B两点，点M的坐标为(2,0).

(2)设O为坐标原点，证明：∠OMA=∠OMB.

解析(2)当l与x轴重合时，∠OMA=∠OMB=0°.当l与x轴垂直时，OM为AB的垂直平分线，所以∠OMA=∠OMB.当l与x轴不重合也不垂直时，设l的方程为y=k(x -1)(k0)，A(x1,y1)，B(x2,y2)，则直线MA,MB的斜率之和为由y1=kx1- k，y2=kx2-k，得将y=k(x-1)代入得(2k2+1)x2-4k2x+2k2-2=0.所以，x1+x2则0.从而kMA+kMB=0，故MA,MB的倾斜角互补，所以∠OMA=∠OMB.综上，∠OMA=∠OMB.

题型六：最值、取值范问题

圆锥曲线最值问题的两种常用解法：

①几何方法，所求最值量具有明显的几何意义时可以利用几何性质结合图形直观求解；

②目标函数法，选取适当的变量，建立目标函数，然后按照求函数的最值方法求解(多涉及二次函数与不等式)，同时要注意变量的范围；

例8(2013年高考新课标II卷理科)平面直角坐标系xOy中，过椭圆0)右焦点的直线交M于A,B两点，P为AB的中点，且OP的斜率为

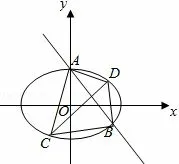
图2

(2)C,D为M上的两点，若四边形ACBD的对角线CD⊥AB，求四边形ACBD面积的最大值.

解析(用点差法求解，过程略)M的方程为

(2)因为CD⊥AB，所以可设直线CD的方程y=x+t，联立消去y得到3x2+4tx+2t2-6=0，因为直线CD与椭圆有两个不同的交点，故Δ=16t2-12(2t2-6)=72-8t2＞0，解-3＜t＜3 ①.设C(x3,y3)，D(x4,y4)，所以因为联立得到解得x=0或所以交点为故因此所以当且仅当t=0 时，四边形ABCD面积的最大值为满足①.即四边形ABCD面积的最大值为

此外，近年高考还出现了探索性问题，将圆锥曲线几何性质与其他的知识融合来考查学生的综合能力.

三、备考建议

基于以上对解析几何考点整理与常见类型题的考查，笔者给出相应的几点备考建议：

1.始于基础，变于基础

近3年全国卷解析几何考查内容源于教材又高于教材，因此，在透彻理解教材的基础上要对教材进行一定变式教学，教会学生灵活应变才是教学的根本所在.故教师在教学过程中要更多在课本练习题狠下功夫，多变式，少“题海战术”，减轻学生负担的同时培养学生的问题分析能力.在回顾基础知识的时候，应该摈弃“填空题”的知识回顾形式，采用“知识环环相扣逐步深化”的提问形式引导学生通过问题引发认知冲突，学会思考，逐步建立知识之间的联系，这样才能更好地帮助学生融会贯通地掌握知识.

2.研究方法与深化思维相结合

解析几何不仅是用代数的方法研究几何的问题，更是从几何的角度处理代数的问题.在解决问题的过程中不仅需要将图形融入坐标系中辅助代数寻找关系，也需要利用圆锥曲线几何性质将代数译成几何，在此过程中几何与代数相辅相成解决问题，这才是解析几何的精髓.

同时，解析几何中存在大量的数学方法，如换元法，配方法，待定系数法及消元法等，在教学的过程中不仅要引导学生能够熟练掌握、运用这些方法，而且要学会在解决问题过程中体会代数与几何之间的转化，以求真正提高学生的逻辑推理与数形分析能力.

3.注重引导一题多解

解析几何注重“以数解形”，从数的角度发现形的关系，但这在一定程度会使学生习惯单从代数计算的角度来推导图形关系，反而容易禁锢学生从几何角度剖析问题的能力，不利于学生逻辑推理能力的发展.

因此在教学过程中注重引导学生一题多解，从多方角度(代数角度与几何角度)思考，同时辅助适当的二级推论，借助几何结合代数寻求更为简便的方法，大大的体现“解析”与“几何”之间的联系(例如本文例2，例3 以及例4 的解法二).这样不仅可以帮助学生快速解决问题，还可以辅助检查前面的计算，同时帮助学生逐渐学会从多角度看待问题，理解问题本质.

4.适当引导学生记忆二级推论

在重视基础的过程中，还要适当引导学生推导、理解、掌握一定的相关二级推论.适当的二级推论不仅可以帮助学生更为透彻理解概念定义的本质，而且可以培养学生尝试从多角度看待问题，开启多种思路，在一定程度上提高客观题解题效率(如本文例2 解法二)与知识的积累.同时提高主观题的思维反应能力，减少计算量(如本文例5 解法二).