破解大小问题的一件利器—从ex ≥x+1 的不等式链说起

广东省广州市第十六中学(510080) 温伙其

ex≥x+1 的解题应用，是某些近年高考真题、各地模拟试题和各种竞赛的理论背景，被称为“指数基本不等式”.它可演绎出很多经典不等式，它们对于函数的大小问题或最值问题，以及数列的放缩证明，提供一种高效简洁的解题办法.

一、来源背景

1.高等数学：泰勒展开式

对于函数f(x)=ex，在x=0 处的泰勒展开式如下：

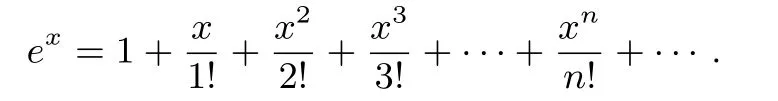
当0＜x＜1 时，有1+x＜ex＜1+x+x2+···+xn+···=上式也可变形为-ln(1-x).

2.中学数学：曲线的切线应用

如图1，知函数y=ex在点P(0,1)处的切线方程为y=x+1，结合y=ex的凹凸性，容易发现ex≥x+1.

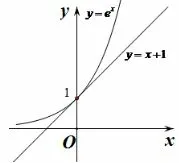
图1

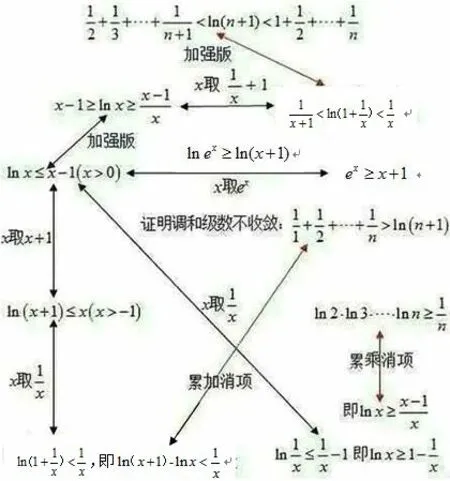
图2

二、演绎变形

由ex≥x+1 出发，通过自然对数运算，结合x用或者1±x代换，可演绎出十分丰富的不等式链，它们及互相关系如图2：

三、不等式链解题应用

上述不等式链中的ex≥x+1 被俗称为指数不等式，lnx≤x-1(x＞0)被俗称为对数不等式，在函数不等式证明和数列放缩法证明中有广泛应用.同时，其它每一个不等式都有强大的功能作用，是破解大小问题的利器.

1.不等式ex ≥x+1 的应用

例1(2014年全国I 卷理第21 题)设函数f(x)=曲线y=f(x)在点(1,f(1))处的切线为y=e(x-1)+2.

(1)求a,b的值；(2)求证：f(x)＞1.

分析(1)解得a=1,b=2，过程从略.

(2)由(1)得f(x)=exlnx+从而f(x)＞1 等价于我们熟悉不等式ex≥x+1，所以ex-1≥x，即ex≥ex，整理有

再由ex-1≥x，得即两边取以e为底的对数，即整理得

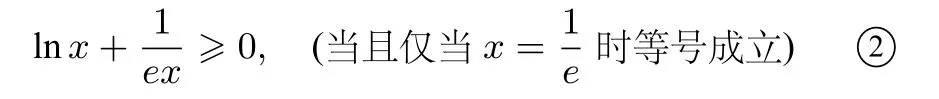
由于① ②两式等号不能同时成立，两式相加得lnx+＞e-x，原不等式得证.

2.不等式ln x ≤x-1(x＞0)的应用

例2(2018年全国I 卷文第21 题)已知函数f(x)=aex-lnx-1．

(1)设x=2 是f(x)的极值点，求a，并求f(x)的单调区间；(2)证明：当a≥时，f(x)≥0．

分析(1)略.(2)当时，有f(x)≥ex-1-lnx-1，我们熟知不等式lnx≤x-1(x＞0)，于是-lnx-1 ≥-x，又有ex-1≥x，所以，ex-1-lnx-1 ≥0，即f(x)≥0.

3.不等式ln(x+1)≤x(x＞-1)的应用

例3(2009年汕头一模理第21 题)设函数f(x)=

(1)令N(x)=(1+x)2-1+ln(1+x)，判断并证明N(x)在(-1,+∞)上的单调性，并求N(0)；

(2)求f(x)在定义域上的最小值.

分析(1)略.(2)我们熟悉不等式ln(x+1)≤x(x＞-1)，所以当x＞-1 时，有所以当且仅当(1+x)即x=0 时等号成立，即f(x)在(-1,+∞)的最小值为0.

4.不等式ln即的应用

例4列{an}满足

(1)求数列{an}的通项公式；

(2)设数列{an}的前n项和为Sn，证明Sn＜n -

分析(1)求得

例5已知函数f(x)=ax+blnx+1，此函数在点(1,f(1))处的切线为x轴.

(1)求函数f(x)的最大值；

(2)当x＞0 时，证明：

(3)已知n ∈N∗,n≥2 时，求证：

分析(1)容易求得a=-1,b=1，函数f(x)的最大值为f(1)=0；

(2)证明：由(1)知f(x)≤0 (当且仅当x=1 时等号成立)，即lnx≤x -1，当x＞0 时，有所以也有所以即整理后有综上可得

(3)由(2)可知当x＞0 时，取x=1,2,3,··· ,n -1,n ∈N∗,n≥2，叠加所得各式，有即成立.

6.不等式≤ln x ≤x-1 的应用

例6(成都市2018 届高中毕业班二诊理科)已知函数f(x)=xlnx+ax+1，a ∈R.

(1)当x＞0 时，若关于x的不等式f(x)≥0 恒成立，求a的取值范围；

(2)当n ∈N∗时，证明：

分析(1)[-1,+∞)，过程从略；

(2)设数列{an}，{bn}的前n项的和分别为则由于an=解得同理所以只需证明我们熟知不等式令则所以所以ln22+下面再证明亦即因为所以只需证现 证 明令h(x)=则h′(x)=所以函数h(x)在(1,+∞)上单调递减，h(x)＜h(1)=0，所以当x＞1 时，2 lnx＜x-恒成立，令则综上，所以 对数列分 别 求 前n项 的 和，得

由此可见，从ex≥x+1 这源头，可演绎变形出丰富有用的不等式链，它们是处理某些不等式问题的有力工具.