T型尾翼布局的垂尾载荷测量技术

张海涛，余建虎，李志蕊，李少鹏，赵燕

中国飞行试验研究院 飞机所，西安 710089

在飞机型号鉴定试飞或合格审定试飞中，飞机结构强度验证是重要的考核项目之一。飞机设计阶段常采用CFD、有限元等方法对其强度及受载状态进行分析和评估，并利用风洞试验进行试验验证，但对于复杂结构的载荷计算结果精度难以保证。中国民用航空规章和国军标明确要求除非表明确定受载情况的方法可靠，否则用以确定载荷大小和分布的方法必须用飞行载荷测量来证实[1-2]。

飞行载荷实测方法包含：应变法[3-5]、压力分布测量[6]、应变天平[7]、光纤测载法[8]、摄影录像法[9]和结构监控[10-11]等。其中应变法由于技术成熟度高，实施较为方便，在实际工程中应用较为普遍。

应变法测载是通过应变电桥测量结构变形，地面校准试验得到应变电桥响应和载荷的数学模型，然后通过飞行试验中得到的应变电桥响应反算出飞行载荷。应变改装位置[5]、校准试验设计和实施[12]、试验数据处理方法[13-18]以及应变电桥的选择[19-20]等均会影响载荷测量精度。

T型尾翼是一种较为常见的尾翼气动布局形式，该布局由于具备使平尾免受机翼机身下洗影响、操作效率高等优点而备受航空界青睐，图154、MD-80、伊尔-76、RJ21-700及中国后续大型运输飞机都采用了T型尾翼布局。但T型尾翼布局飞机尾翼受载复杂，常规的理论计算和地面验证试验并不可靠，需要通过飞行载荷实测来验证优化结构强度和理论计算模型。国内在T型尾翼布局垂尾载荷测量方面尚无公开文献，亟需进行深入研究。

本文将利用应变法对T型尾翼布局垂尾载荷实测方法进行研究，并分析平尾载荷对垂尾载荷的影响。

1 平尾对垂尾受载的影响

T型尾翼布局的飞机平尾安装在垂尾的翼尖处，平尾载荷通过垂尾传递到机身上。这就造成垂尾结构受载复杂，除承受自身惯性力和气动力外，还承受来自平尾的惯性力和气动力。在飞行中一旦出现垂尾、平尾受载严重状态如偏航、俯仰和大侧风等机动时，尾翼结构往往要经受很大考验。

图1为典型T型尾翼布局结构示意图。从局部放大图可知，平尾中央翼盒通过3个铰接连接点与垂尾固定连接，其中连接点1和连接点2位于平尾中央翼盒后缘；连接点3位于平尾中央翼盒前缘，它通过螺旋驱动器连接，可以上下伸缩，这种连接方式即能实现平尾与垂尾的固定连接，又可实现平尾安定面随着指令变化上下偏转。

T型尾翼布局飞机平尾受载对垂尾载荷的影响参见图2的简化理论受载模型。假定平尾半翼展长度为a，当平尾受到均布对称载荷q时，平尾传递到垂尾的载荷为:沿轴向拉压载荷FV=2qa，侧向弯矩MV=0，侧向剪力SV=0；而左右平尾受到不同的分布载荷p、q时，平尾不仅传递给垂尾沿轴向的载荷FV=(p+q)a，而且传递给垂尾侧向的弯矩MV=0.5(p-q)a2，侧向剪力SV=0。

通过理论分析发现，平尾传递到垂尾上的载荷主要为轴向拉压载荷FV和非对称受载下的侧向弯矩MV。而飞机轴向拉压承载能力很强，一般不作考核，因此，针对T型尾翼布局飞机平尾对垂尾载荷的影响研究主要集中在侧向弯矩MV。

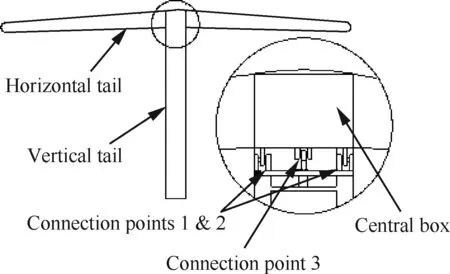
图1 T型尾翼结构示意图Fig.1 Schematic diagram of T-shaped empennage structure

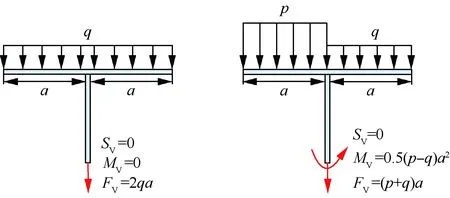
图2 T型尾翼简化受力模型Fig.2 Simplified load model of T-shaped empennage

通过上述分析，为准确捕捉平尾传递到垂尾上的非对称弯矩载荷，在如图3所示的平尾中央翼盒布置应变电桥，该电桥对平尾对称载荷不敏感，而对非对称载荷敏感。

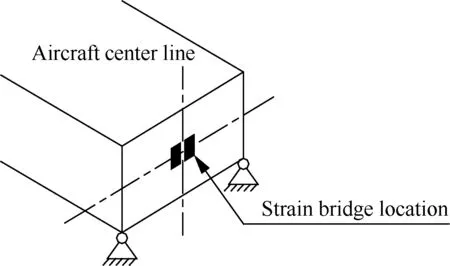
图3 平尾中央翼盒应变电桥位置Fig.3 Location of strain bridge of horizontal tail central box

2 校准试验

2.1 试验设计

常规布局尾翼由于平尾和垂尾受载相对独立，在进行校准试验设计时仅考虑自身翼面的受载，显然该思路不适用于T型尾翼布局下受平尾影响的垂尾校准试验设计。

为充分考虑T型尾翼布局下平尾对垂尾侧向弯矩的影响，设计了平尾非对称校准加载工况。本文以某型T型尾翼布局飞机垂尾弯矩载荷测量为例进行说明。为了更真实地模拟T型尾翼布局飞机垂尾受载状态，设计了垂尾侧向加载工况18个、平尾非对称加载工况14个、平尾对称加载工况20个，详见表1，加载点位置及应变电桥位置见图4和图5。

表1 校准工况分类统计Table 1 Classification statistics of calibration condition

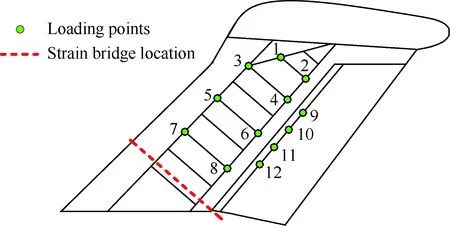
图4 垂尾应变电桥位置及加载位置Fig.4 Location of strain bridge of vertical tail and loading points

图5 平尾应变电桥位置和加载位置Fig.5 Location of strain bridge of horizontal tail and loading points

2.2 试验实施

T型尾翼载荷校准采用液压自动加载系统加载。平尾校准工况利用卡板向下加载，垂尾利用专用加载台架加载。图6和图7分别为平尾和垂尾校准试验加载。

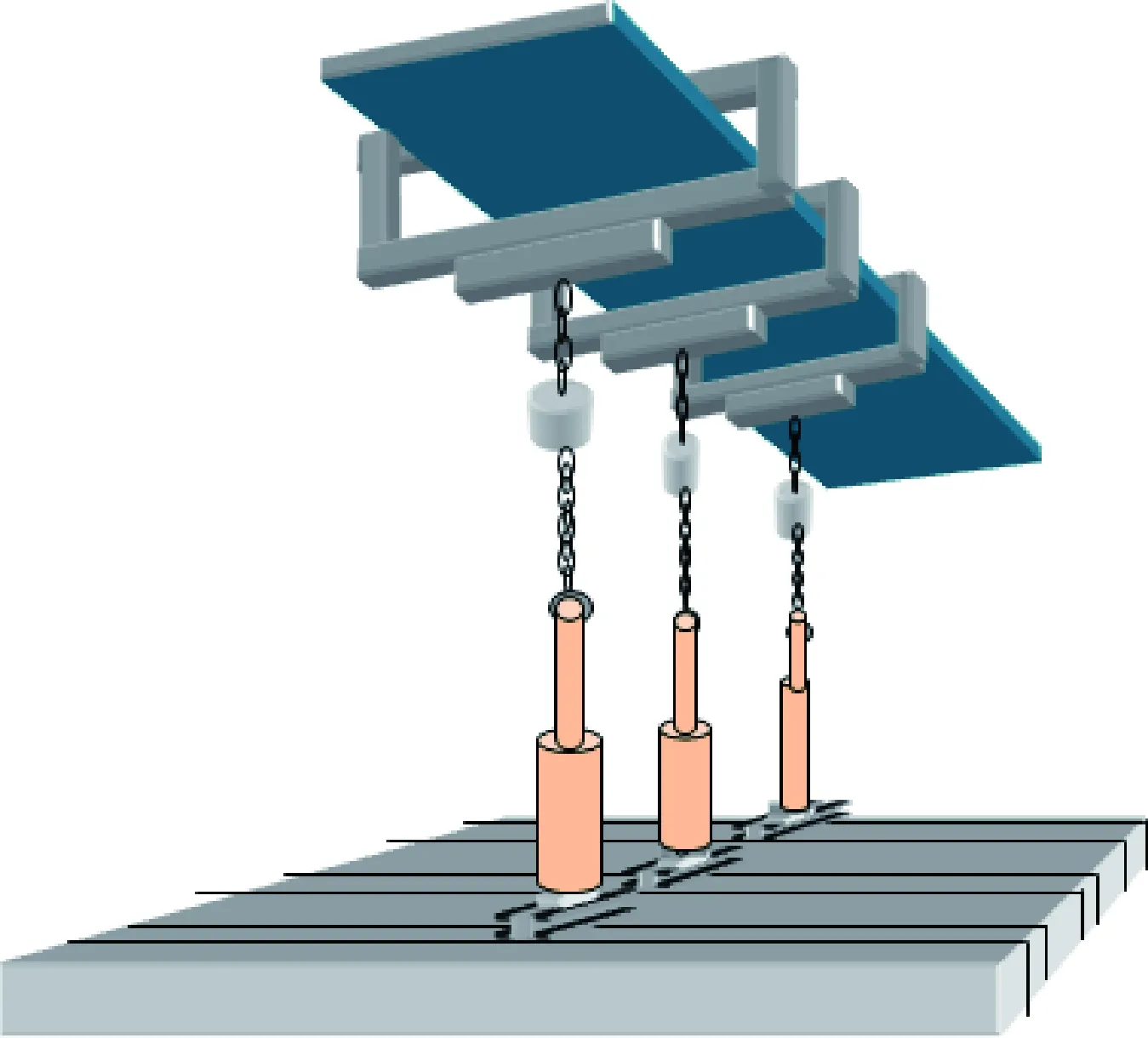
图6 平尾校准示意图Fig.6 Schematic diagram of horizontal tail calibration

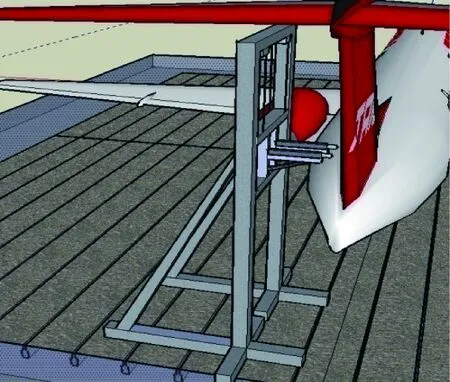
图7 垂尾校准示意图Fig.7 Schematic diagram of vertical tail calibration

2.3 试验结果

2.3.1 应变响应

通过试验加载，得到了垂尾和平尾应变电桥数据。

1) 垂尾应变响应

图8为垂尾弯矩电桥响应随平尾校准载荷F的变化曲线，图中：ε1为垂尾前梁弯矩，ε2为垂尾后梁弯矩，HTSL为平尾对称加载，HTUL为平尾非对称加载，VTL为垂尾加载。在平尾对称加载时，ε1和ε2电桥响应很小，而在平尾非对称加载和垂尾加载时电桥响应明显与载荷线性相关，且线性度和单一性均很好，说明垂尾弯矩电桥对垂尾载荷和平尾非对称载荷敏感，对平尾对称载荷不敏感。

图9为垂尾电桥响应系数R[14]随加载点到测载剖面距离d的变化曲线。图中HTFUL为平尾前梁非对称加载、HTBUL为平尾后梁非对称加载、VTFL为垂尾前梁加载、VTBL为垂尾后梁加载。可看出在平尾非对称载荷工况和垂尾加载工况下，垂尾弯矩电桥ε1和ε2的响应系数R与距离d明显线性相关。

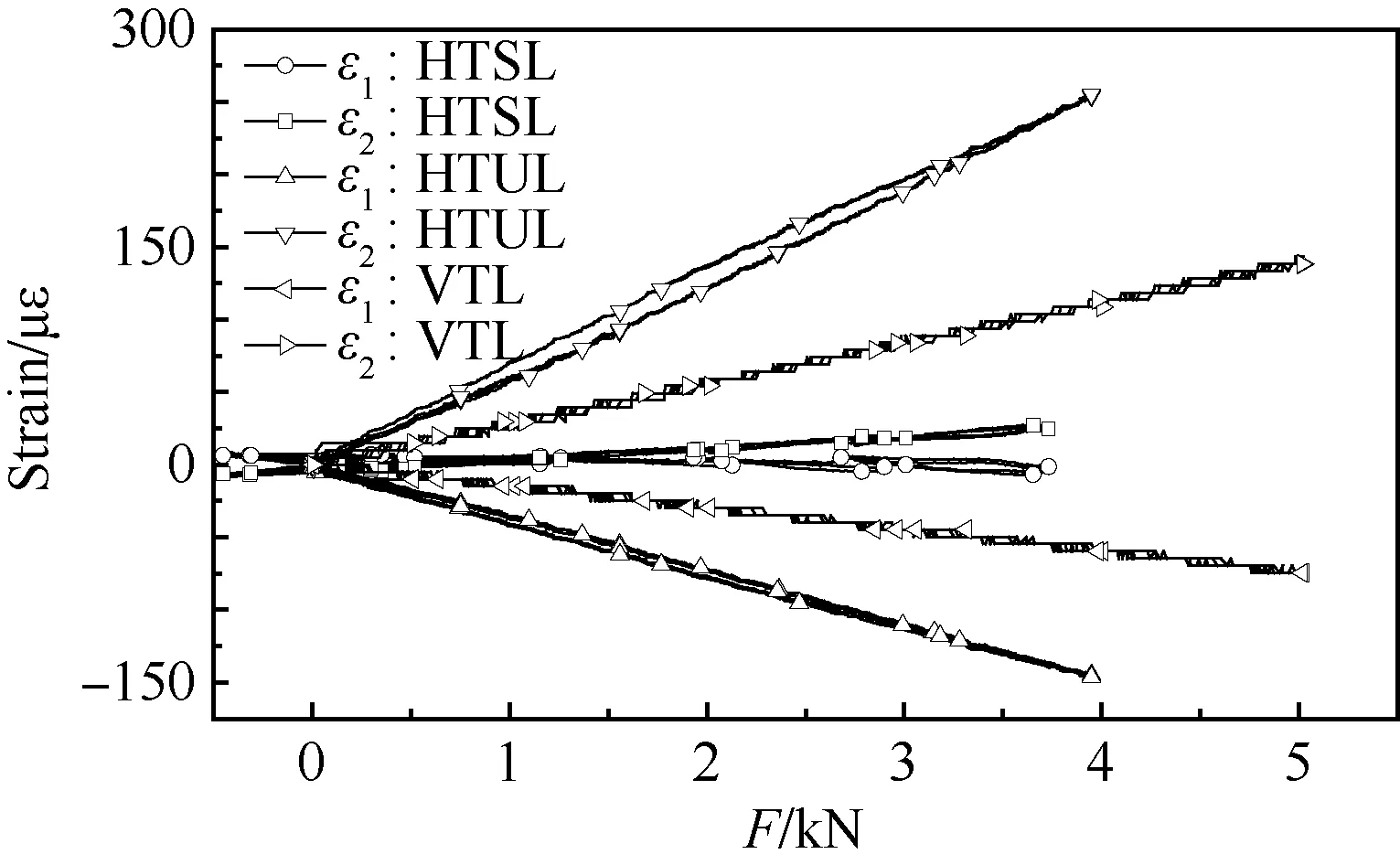
图8 垂尾应变电桥响应随平尾校准载荷变化Fig.8 Vertical tail strain bridge response vs horizontal tail calibration load

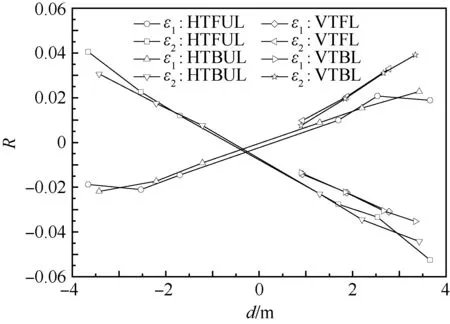
图9 垂尾应变电桥响应系数随距离的变化Fig.9 Vertical tail strain bridge response coefficient vs distance

综合图8和图9可得出，垂尾电桥ε1和ε2响应与平尾非对称弯矩及垂尾弯矩线性相关，这与理论受力分析结果完全相同。因此垂尾载荷建模时需要将平尾非对称工况引入垂尾载荷方程建模，才能更加真实模拟T型尾翼布局下的垂尾受载。需要指出的是此时测量的垂尾弯矩包含垂尾弯矩和平尾传递给垂尾的弯矩。为了准确得到垂尾弯矩，可利用平尾中央翼盒应变电桥分离出平尾传递给垂尾的弯矩。

2) 平尾中央翼盒应变响应

平尾中央翼盒应变电桥ε3在平尾对称加载和非对称加载时的应变电桥响应如图10所示。图11为电桥ε3在平尾前、后梁非对称加载时响应系数随加载点到测载剖面距离d的响应曲线。

图10 平尾应变电桥响应随平尾校准载荷的变化Fig.10 Horizontal tail strain bridge response vs horizontal tail calibration load

从图10和图11中可明显看出，平尾中央翼盒处应变电桥与平尾非对称弯矩具有强线性关系，因此可使用该电桥测量平尾非对称弯矩。

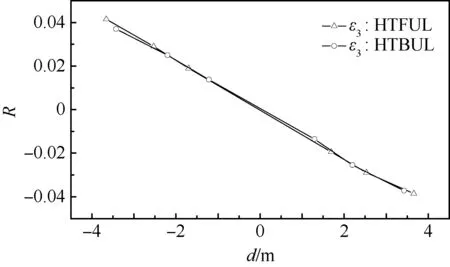
图11 平尾应变电桥响应系数随距离的变化Fig.11 Horizontal tail strain bridge response coefficient vs distance

2.3.2 载荷方程建模

常规的载荷建模过程中仅使用垂尾校准工况，载荷模型[4]为

(1)

本文在进行垂尾载荷建模时引入了平尾非对称载荷工况，考虑了平尾载荷对垂尾的影响，使垂尾载荷模型样本更加丰富，更加符合T型尾翼结构飞机垂尾的真实受载，载荷模型为

(2)

式中：MVi、MHi分别为垂尾和平尾校准工况加载时对应的弯矩载荷；ε为应变电桥响应；K为载荷方程的系数矩阵；s为引入载荷方程的垂尾应变电桥数量；n、m分别为垂尾和平尾校准工况数量；Vi、Hi分别为垂尾和平尾校准工况。

将对应的试验校准数据分别代入式(1)、式(2)中，利用最小二乘法即可得到系数矩阵K，从而得到两种不同的垂尾弯矩方程。为了实测平尾非对称弯矩，利用平尾中央翼盒处应变电桥建立了平尾非对称弯矩方程。具体载荷模型及误差见表2。

表2中MV1为利用垂尾常规建模方法得到的载荷方程，MV2为引入平尾非对称载荷时新的垂尾建模方法得到的载荷方程，MH为平尾非对称弯矩载荷方程。从试验结果可以明显看出，载荷方程MV2比MV1的校准结果精度提升了2.16%，说明本文提出的方法是有效的。

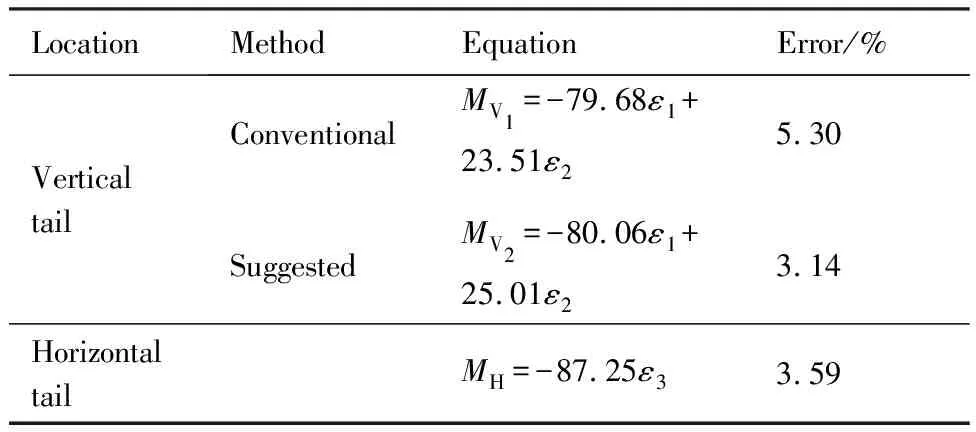
表2 T型尾翼载荷方程Table 2 Equations for T-shaped empennage load

3 飞行试验

使用本文方法测量分析偏航机动和滚转机动下T型尾翼受载严重时的垂尾弯矩。

在高度H=30 000 ft(1 ft=0.304 8 m)、马赫数Ma=0.82时执行偏航机动，飞行参数及载荷时间历程如图12所示，其中Ny为飞机侧向过载。随着方向舵开始偏转，飞机侧滑角和侧向过载逐渐变大，垂尾根部弯矩MV2和平尾非对称弯矩MH随之增加。对平尾非对称弯矩和垂尾根部弯矩进行对比分析可发现，平尾非对称弯矩对垂尾根部剖面弯矩影响十分显著，平尾最大不对称弯矩占垂尾根部弯矩的57.6%。

图12 偏航机动时间历程Fig.12 Yaw maneuver time course

在高度H=30 000 ft、Ma=0.82时执行滚转机动，飞行参数及载荷时间历程如图13所示。随着左右副翼开始偏转，滚转角逐渐增大，平尾非对称弯矩MH和垂尾根部弯矩MV2均显著增大，平尾最大非对称弯矩占垂尾根部弯矩的61.9%。

图13 滚转机动时间历程Fig.13 Roll maneuver time course

4 结 论

1) 具有中央翼盒的平尾结构，在中央翼盒处进行应变改装可有效测得平尾非对称载荷。

2) 通过试验证明，本文提出的测载方法有效可靠，载荷方程误差由5.30%降至3.14%，该方法可用于后续其他飞机T型尾翼载荷实测。

3) T型尾翼布局飞机平尾不对称弯矩载荷对垂尾弯矩影响十分显著，偏航机动严重受载状态时可达到垂尾弯矩的57.6%，滚转机动严重受载状态时可达到垂尾弯矩的61.9%。