三角翼DBD等离子体流动控制研究进展

牛中国，赵光银,*，梁华，柳平

1. 空军工程大学 航空工程学院 等离子体动力学重点实验室，西安 710038 2. 重庆交通大学 航空学院，重庆 400074

三角翼布局的优点是超声速飞行时阻力低、失速迎角相对较大，因此多用于现代战斗机的设计。大后掠角低展弦比三角翼适用于高速飞行器[1]；中小后掠角低展弦比机翼常用于微型飞行器和无人轰炸机等[2]。然而，三角翼布局相对低的升阻比不利于长航程的设计需求，升力系数曲线斜率较缓意味着其在起飞/着陆阶段产生的升力较低，大迎角时翼尖的抖振也较为严重。三角翼在较大迎角绕流时往往表现出涡流主导的绕流特性，空气动力特性受涡结构影响较大。控制这些涡流具有诸多意义[3]，例如增加升力和提高临界迎角、产生用于飞控的操纵力矩、减缓机翼或尾翼的振动。

前缘涡结构受三角翼几何构型影响较大，尤其是前缘后掠角的影响[3]。图1给出了不同后掠角三角翼失速特性[3-7](图中α为迎角，CL为升力系数)。对于细长三角翼(后掠角Λ≥65°)，涡破裂的发生点距失速边界很近，这意味着涡破裂导致的涡升力的丢失影响着机翼的最大升力系数和失速；细长三角翼涡破裂点的前后不稳定移动范围可达10%弦长，会引起气动力和力矩振荡[6]。当涡破裂发生在非细长三角翼上(Λ∈[35°，55°])时，升力系数仍可近似线性地增大到较大迎角下(图1(c))，这意味着涡破裂并非影响非细长三角翼大迎角空气动力特性的主导因素，近失速时翼面上的旋涡难以附着到翼面上可能是其失速的主要原因。因此，对脱体涡流型的流动控制与后掠角有较大关系。

近几年，较多的试验和仿真研究了三角翼前缘涡的控制，控制方式有机械式和气动式，比如多涡系、控制舵面、吹吸气、低频和高频激励、反馈控制、柔性机翼、等离子体激励等。这些控制方式的概念和控制机理在文献[3]中进行了详细的阐述。边条翼、鸭翼产生涡流通过多涡耦合干扰控制，增强前缘涡的稳定性和强度，结构简单，使用可靠，目前很多战斗机仍在使用；前缘吹气、尾缘射流、吹吸气等控制方式，需要比较复杂的气路，难以产生响应快、频带宽的激励，而且气源也是一个问题；前缘涡襟翼、尖顶襟翼则需要复杂的机械装置。因此，迫切需要探索新的三角翼前缘涡控制技术。

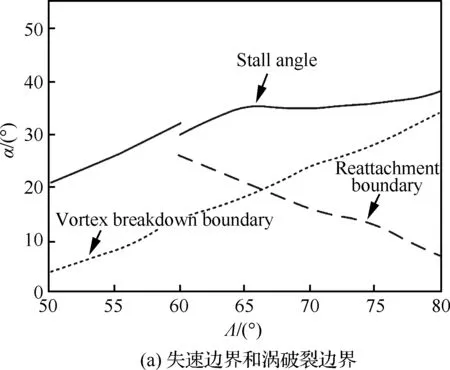
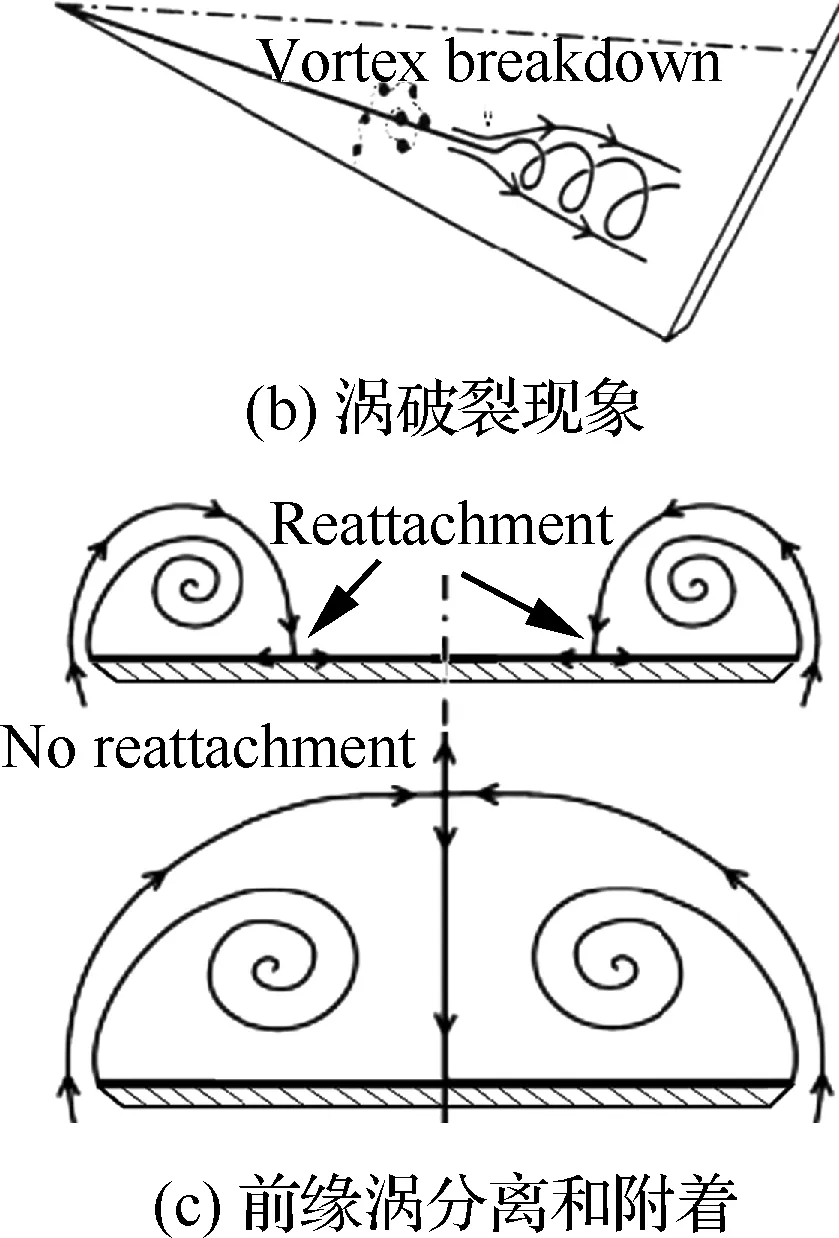
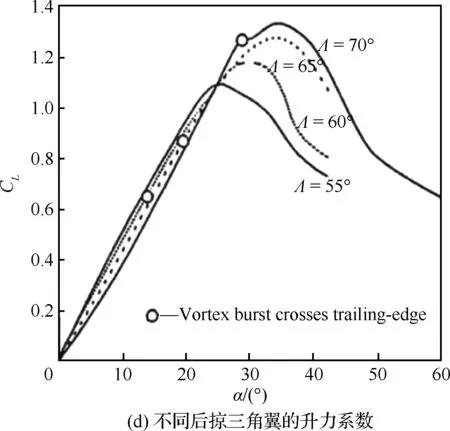
图1 不同后掠角三角翼的失速特性[3-7]Fig.1 Stall characteristics of delta wings with different swept angles[3-7]

等离子体流动控制是基于“等离子体气动激励”的新概念主动流动控制技术，与传统流动控制手段相比，易于产生快速(<0.1 ms)、可控的宽频带气动激励(0.01～100 kHz)，结构简单，不改变原有气动型面，有望解决其他流动控制手段不能解决或难以解决的快速主动控制等问题，进而为流动控制方式从固定的开环控制向自适应的闭环控制转变提供良好的基础条件。

1 DBD等离子体气动激励

放电原理不同，可产生不同形式的等离子体气动激励，比如用于流动分离控制的表面介质阻挡放电(Surface Dielectric Barrier Discharge, SDBD)激励[8]，用于激波控制的表面电弧放电激励[9]，基于弧光放电和火花放电原理产生的等离子体合成射流激励[10]等。文献[11]就多种典型等离子体气动激励的特性和应用，综述了等离子体流动控制的研究进展。对于分离流控制和旋涡控制，常用的SDBD等离子体激励器，如图2所示。典型的常用SDBD激励器是由高低压电极非对称地粘贴于绝缘介质层两侧构成的，介质层的作用是防止微放电向热电弧转化，有利于产生大区域相对均匀的等离子体。

根据施加于激励器上的电压信号，可产生流动控制常用的4种DBD激励：连续模式的AC-DBD (Alternating Current-DBD)，脉冲调制模式的AC-DBD(如图3(a)所示，图中AM表示正弦波调制，BM表示脉冲调制)，微秒脉冲DBD(μs-DBD)[12]，纳秒脉冲DBD (NS-DBD)[13-14](如图3(b)所示)。相对于高频连续模式的AC-DBD激励，脉冲调制模式的AC-DBD、μs-DBD和NS-DBD的脉冲频率要低1～2个数量级，相对于低速流动，具有明显的非定常性，这里称为非定常激励；相对地，将高频连续模式的AC-DBD激励称为定常激励。

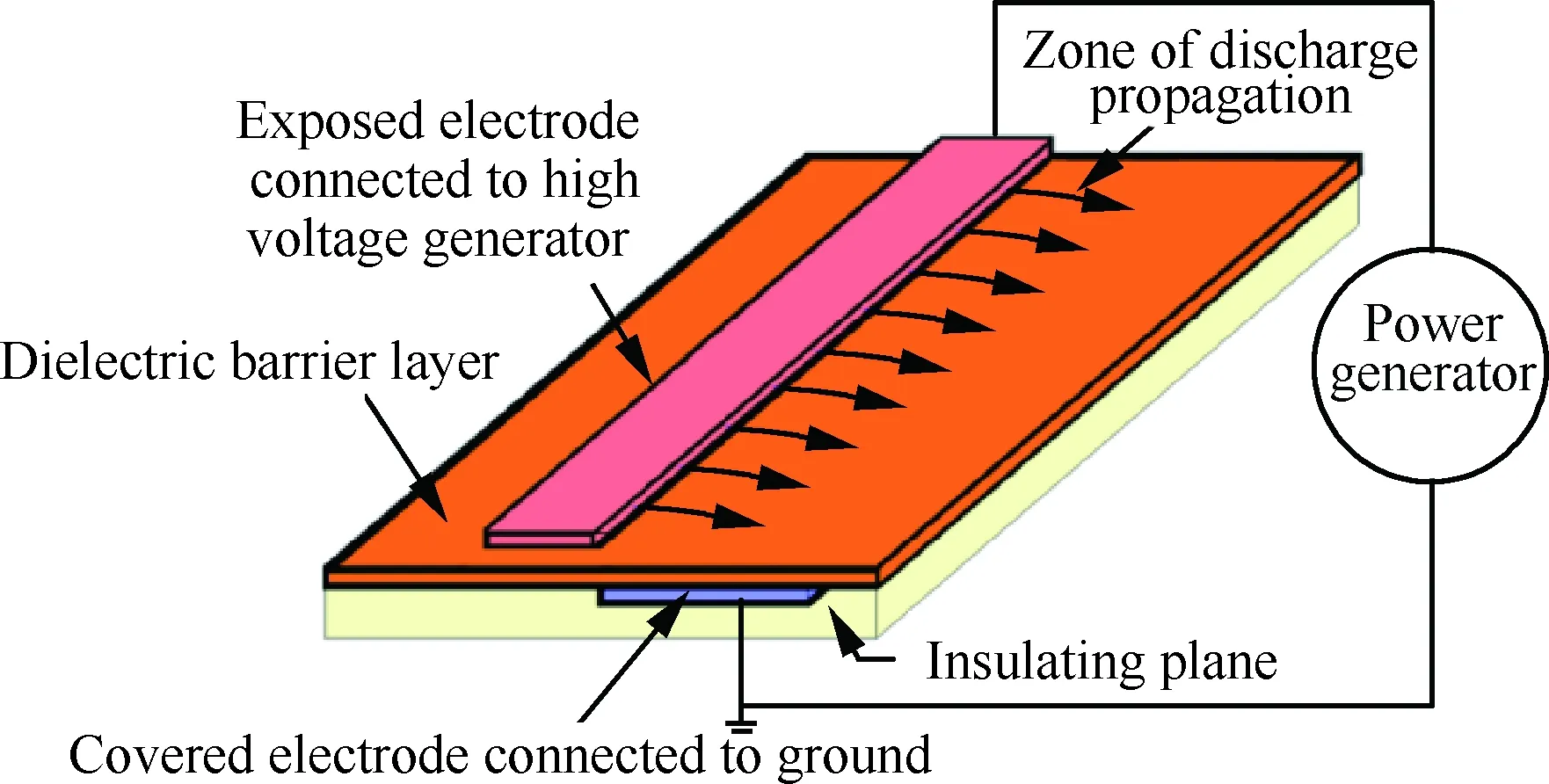
图2 流动控制中典型的SDBD激励器示意图Fig.2 Schematic of typical SDBD actuator in flow control

图3 激励器上典型电压波形Fig.3 Typical voltage waveforms applied to actuator

文献[15-18]对不同时间尺度DBD激励的放电特性和诱导流动特性进行了研究，发现不同激励诱导的扰动形式有本质不同，如图4所示(图中d为高低压电极垂直间距)。AC-DBD激励可看作体积力源，定常AC-DBD激励主要诱导近壁面射流，而非定常AC-DBD激励在一定条件(合适的频率和占空比)下可诱导周期性启动涡。NS-DBD激励向流场注入很小的动量，却可诱导形成冲击波，原因是部分放电能量在短时间(<1 μs)转为热能，瞬间局部放热诱导冲击波。相比AC-DBD，NS-DBD诱导速度很低(0.5 m/s以下)，可看作一个瞬间热量源。文献[15]对不同时间尺度DBD激励的电特性和体积力特性进行了测试，发现μs-DBD最大放电电流和诱导体积力介于AC-DBD和NS-DBD之间。空军工程大学等离子体动力学重点实验室的相关研究表明：μs-DBD激励单脉冲放电能量介于AC-DBD和NS-DBD之间，可诱导周期性旋涡和冲击波结构产生[16]，表明μs-DBD激励可诱发体积力和热两种扰动形式。μs-DBD的脉冲激励电压上升沿在微秒尺度，使其电磁干扰比NS-DBD低得多。

图4 不同时间尺度DBD激励诱导流场结构Fig.4 Induced flow structure by DBD actuation at different time scales

关于AC-DBD近几年在流动控制中的发展、新型设计、创新应用，文献[19-21]分别进行了综述。激励诱导最大速度限于绝缘材料和激励器结构，体积力作用主导的AC-DBD激励诱导速度较低(<10 m/s)，流动控制能力较弱。在追求表面DBD控制高速分离流的研究中，逐步认识到，非定常等离子体激励的控制能力优于定常激励[22]；相比AC-DBD和μs-DBD，NS-DBD流动控制能力得到巨大提升[23]。NS-DBD激励已被验证在起飞着陆马赫数和雷诺数下能够推迟机翼失速[24]，在马赫数Ma=0.74下可有效抑制翼型绕流分离[13]，在高马赫数下可有效控制脱体激波强度和位置[25-26]，在Ma=0.5下可有效改善超临界翼型和飞翼布局的气动特性[27]。然而，文献[14]比较了二者控制效果，发现在前缘分离控制能力上AC-DBD不如NS-DBD，后缘分离控制却好于NS-DBD；且低速下二者均可取得很好的前缘分离控制效果，所以孰优孰劣，不能一概而论。相对而言，μs-DBD在流动控制中研究相对较少。

2 DBD激励三角翼前缘涡控制研究现状

表面DBD激励用于三角翼前缘涡控制，还未得到广泛研究。已有研究多采用AC-DBD激励，且多以大后掠角尖前缘三角翼为研究对象。第1节所述4种DBD激励形式中，定常和非定常AC-DBD激励在三角翼涡控制中研究得最为深入和广泛[4,28-31]，μs-DBD和NS-DBD用于三角翼涡控制相对较少[32-34]。

以色列理工学院Greenblatt等[28]与柏林科技大学合作试验研究了非定常AC-DBD激励对60°后掠角三角翼前缘涡结构的影响，表明控制效果依赖于无量纲激励频率F+(F+=fc/U∞，其中，f为脉冲激励频率，c为机翼根弦长，U∞为来流速度)，当F+≈1时对前缘涡的控制作用最好。圣母大学Kwak和Nelson[4]进行了AC-DBD激励改善三角翼气动特性的低速风洞试验。试验研究了两种不同的激励器布局对后掠角分别为55°、65°和75°的尖前缘三角翼的流场结构和气动特性的影响，发现流动控制效果受三角翼后掠角的影响很大。俄罗斯科学院Sidorenko等[30]研究了AC-DBD激励对65°后掠角三角翼流场结构的影响，发现激励可影响前缘涡的稳定性。美国空军研究实验室Visbal和Gaitonde[35]开展了AC-DBD激励控制75°后掠角三角翼流动的数值模拟研究，在上翼面机翼顶点附近施加AC-DBD激励可显著推迟前缘涡破裂。美国轨道研究所Patel等和圣母大学合作[29]，采用AC-DBD激励，在47°后掠角1303无人机上进行等离子体流动控制风洞试验，发现在较广的迎角范围内，通过前缘涡和尾缘环量控制，空气动力特性得到较大变化，有望实现用于航空器控制的无铰链等离子体襟翼。日本国立鸟取大学Matsuno等[36]开展烟流显示试验表明了新型激励器对于60°后掠角尖前缘三角翼的前缘涡控制是有效的。

香港理工大学Shen等[37]在雷诺数Re=5×104、后掠角75°三角翼上开展了AC-DBD激励进行流动控制的试验研究，发现单侧前缘激励可促进同侧前缘涡破裂，同时推迟了异侧前缘涡的破裂，天平测力发现DBD激励使力矩产生明显改变[38]，预示着用DBD激励控制三角翼的机动是有潜力的。北京航空航天大学Zhang等[31]试验研究了AC-DBD激励对75°后掠角三角翼气动特性和流场结构的影响。在不同弦向位置施加AC-DBD激励均可增大升力系数；烟流显示表明38°迎角下40%弦长处的激励可将涡破裂位置由0.68弦长处推迟到0.76弦长处。空军工程大学与中航工业空气动力研究院合作，进行了三角翼等离子体流动控制的初步试验研究[33,39]。在47°后掠角的钝前缘三角翼上，首次采用NS-DBD激励，通过天平测力研究了激励位置、激励电压、激励频率对流动控制效果的影响规律，在来流50 m/s 下取得了较好的控制效果。

3 研究现状总结分析

由于DBD激励属于气动式的，其在三角翼涡控制上的常见布局与气动式的吹吸气有很多相似之处；同时根据研究现状，发现主要有4种DBD激励器布局较多地用于三角翼涡控制(见图5)：① 激励器布置在机翼前缘[4,28](图5(a))，研究认为脉冲放电引入前缘非定常扰动比连续式放电效果好，最佳无量纲激励频率F+≈1；② 激励器布置在垂直于前缘[4,30]以诱导附面层向下游加速(图5(b))，研究认为定常AC-DBD激励效果好于非定常激励，顺气流方向的连续激励可推迟旋涡破裂，逆气流方向的连续激励可导致旋涡提前破裂[30]；③ 激励器沿二次分离线布置[30](图5(b))，形成展向的等离子体射流，研究认为该布局的非定常激励对旋涡稳定性有效果；④ 激励器布置在上翼面不同弦向或垂直于翼根(图5(c))，诱导沿涡轴向的加速[31,35]，可推迟涡的破裂，与图5(b)作用类似。

由于DBD诱导气流速度较低，其激励布局还不同于吹气激励(比如在尾缘诱导喷流进行环量控制上还不能像吹气那样)，因此DBD激励器的布局有其独特之处。表1[4,27-35，38，40-42]给出了近年来三角翼等离子体流动控制研究对应的试验状态，可以看出目前研究多是在雷诺数和来流速度较低(<30 m/s)条件下进行。分析原因可能一方面是AC-DBD产生的扰动强度不足，在较高雷诺数和来流速度下难以起到明显的控制效果；另一方面，国外部分研究以微型无人飞行器流动控制为研究背景，相对应的雷诺数低。

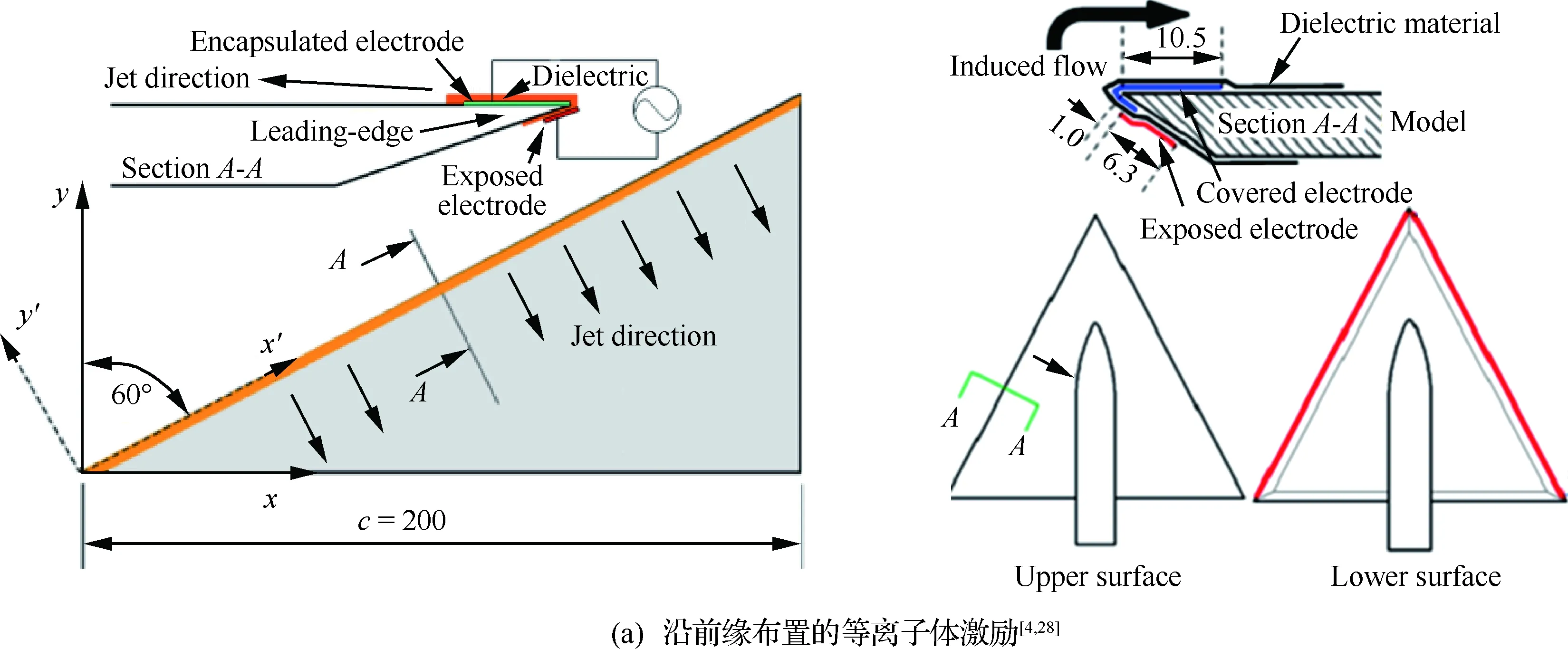
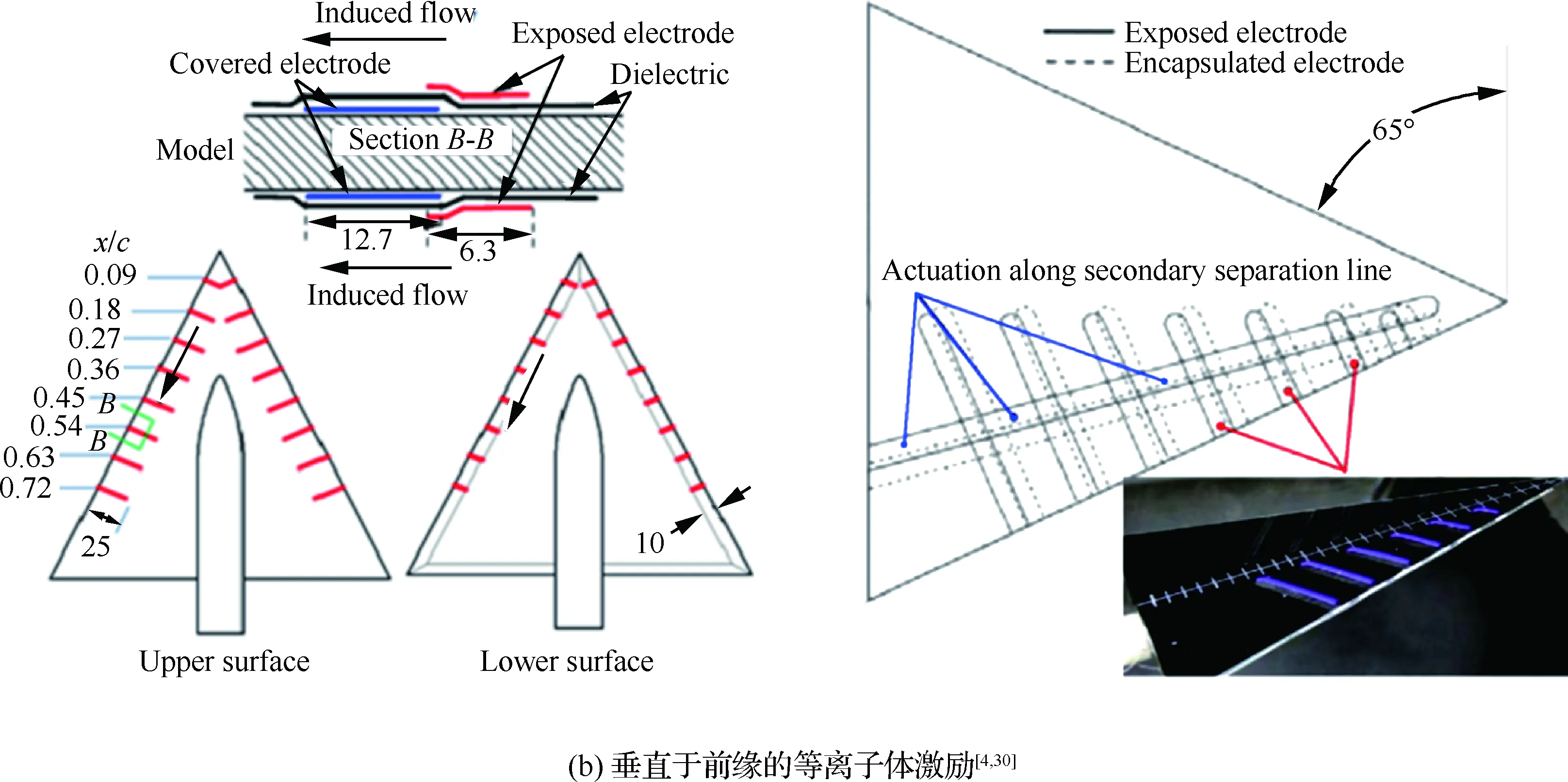
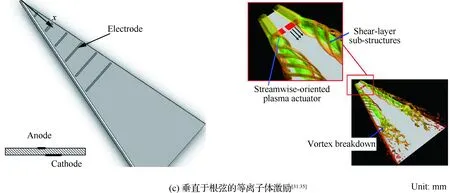
图5 三角翼流动控制常用的等离子体激励器布局Fig.5 Common arrangements of plasma actuator in delta-wing flow control research

图5中，DBD等离子体激励用于三角翼流动控制研究均取得一定控制效果，前缘激励主要利用非定常等离子体激励诱导非定常扰动效应，起到增强前缘涡强度的效果，对非细长三角翼有良好的控制效果[4]；上翼面不同弦长激励主要利用定常激励对流场的加速效应，起到推迟脱体涡破裂的目的，对细长三角翼有良好的控制效果[4,31]。总的来说，AC-DBD激励对三角翼涡流场有效控制的来流速度较低。NS-DBD激励用于外流控制的研究多围绕翼型开展，三角翼流动控制的研究不多；与AC-DBD激励相比，可控速度已有大幅提升。下面就定常激励和非定常激励两方面，进一步分析影响三角翼流动控制效果的因素。

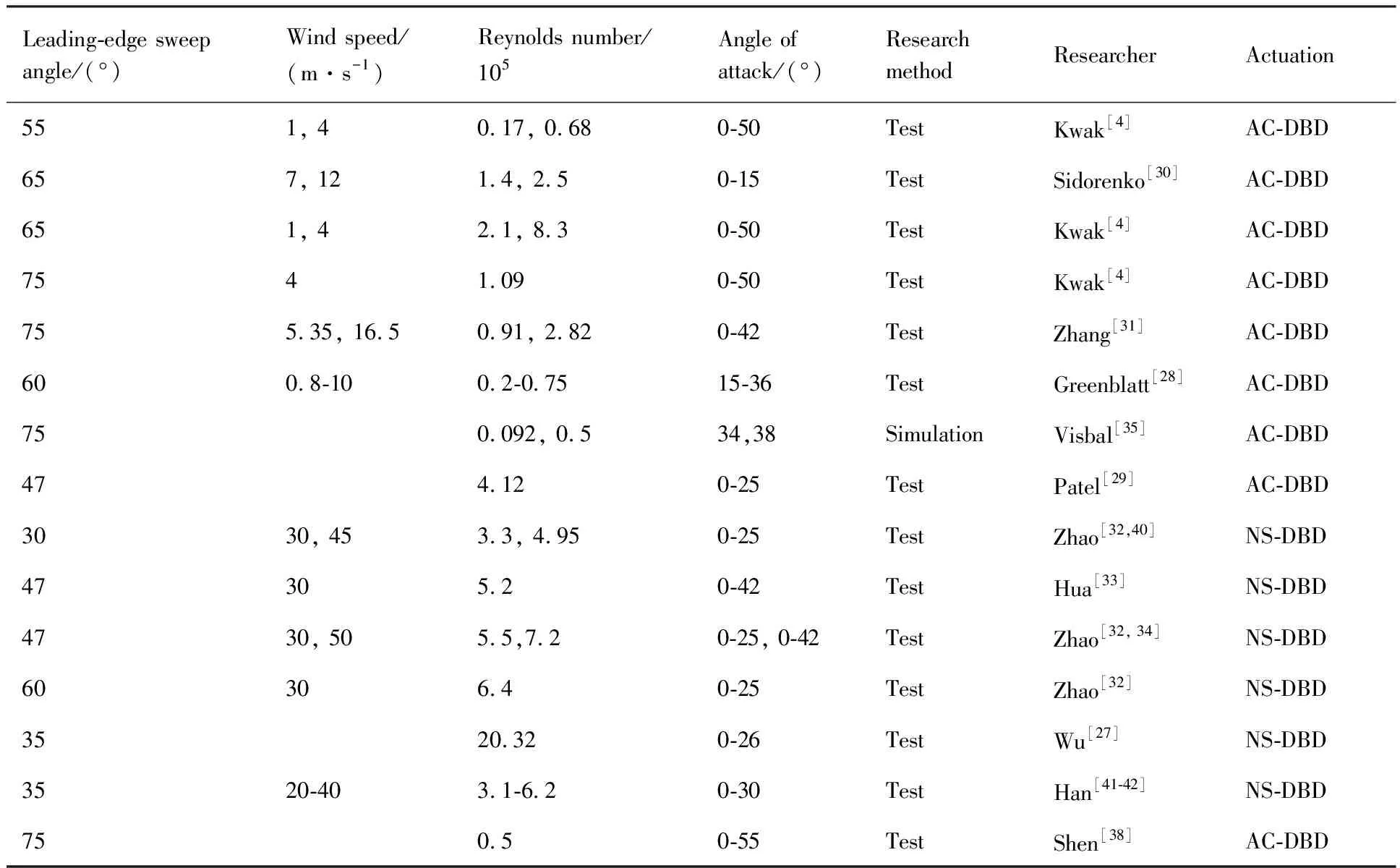
表1 三角翼等离子体流动控制的研究情况Table 1 Studies of delta-wing flow control by plasma actuation

4 定常激励下影响控制效果的因素

这里定常激励是连续AC-DBD，其可诱导近壁面射流，起到加速附面层内低速流体的作用，类似于定常吹气的激励方式。根据目前研究结果，主要从激励位置和激励电压两方面论述。

4.1 激励位置的影响

对于定常模式的AC-DBD激励，文献[4]进行了不同后掠角(Λ=55°，65°，75°)三角翼流动控制的试验，发现其在前缘的激励无明显控制效果；而且垂直前缘处诱导向下游加速的激励布局(图5(b))，也仅在大后掠角机翼上取得效果，使涡破裂点得到推迟。由于相关研究较少，多数试验研究选用的后掠角相对较大，所得结论尚需进一步验证。

诱导向下游加速的激励在文献[4,31,35]也取得明显控制效果(图5(c))，也是在大后掠角三角翼上取得；图5(b)和图5(c)布局虽不同，对于连续AC-DBD，均可诱导沿涡轴向加速的分量体积力。对于中小后掠角机翼，这两种布局却未取得明显控制效果,原因可能与不同后掠角三角翼的绕流特性有关。对于大后掠角的三角翼，涡破裂是其失速的主要原因,诱导向下游加速的激励可以增大旋涡轴向速度，减小涡比(旋涡旋转速度与轴向速度之比)，从而推迟涡破裂。

4.2 激励电压的影响

5 非定常激励下影响控制效果的因素

三角翼绕流控制常用的非定常DBD激励有3种：非定常AC-DBD、μs-DBD、NS-DBD。文献[33]通过测力方式系统研究了NS-DBD激励位置对带三角翼的翼-身组合体升力特性的改善效果，发现最佳位置在前缘。值得一提的是文献[30]采用非定常AC-DBD激励，发现沿展向二次分离线的激励虽未能提高升力系数，却对前缘涡稳定性有益。结合图5给出的常见激励布局，就非定常激励而言，从升力特性改善的角度看，最佳的激励位置在最前缘。

前缘激励主要是利用等离子体激励形式的扰动，在合适的激励频率下，激励可激发前缘剪切层不稳定性，促进剪切层两侧流体动量能量掺混[2-3]。这里就前缘非定常激励下，讨论来流条件、几何构型、激励参数等方面因素对控制效果的影响。

5.1 来流条件的影响

来流条件主要是来流速度，其对雷诺数的影响较大。对于尖前缘三角翼，前缘涡特性对雷诺数的依赖较小[45]。对流动控制而言，前缘涡对非定常激励的响应却与来流速度关系较大。图6为不同雷诺数下前缘非定常AC-DBD激励引起的三角翼法向力系数变化量(ΔCN)和升力系数(ΔCL)的变化量。随雷诺数增大，升力系数增量减小；Re=75 000时的增量已远不如Re=20 000。

一般而言，低速下不考虑压缩性的影响，速度增大导致雷诺数增大，而速度增大意味着来流具有较大的动量和能量；对于同样能量强度的激励，当来流速度增大，则意味着其相对来流的扰动强度降低了。

文献[27,41]对后掠角35°的飞翼布局进行流动控制，发现来流速度为20～40 m/s时最大升力系数可提高20%以上；Ma=0.4时，最大升力系数提高约5%，远低于低速下最大升力系数的提高量，说明来流速度高，控制效果弱。

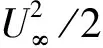
图6 机翼失速时AC-DBD激励前后的法向力系数和升力系数变化[28]Fig.6 Variation of normal force coefficient and lift coefficient before and after AC-DBD actuation with wing at a post-stall angle of attack

5.2 几何构型的影响

根据国内外研究结果，发现三角翼前缘后掠角和前缘截面形状对流动控制效果影响较大。

5.2.1 后掠角

普遍认为，后掠角Λ=60°是处于细长三角翼(Λ≥65°)和非细长三角翼(Λ∈[35°,55°])的过渡状态[2-3]。文献[40]在Λ=30°尖前缘三角翼上采用前缘NS-DBD激励取得了良好的前缘涡控制效果；文献[32-34,29]在Λ=47°三角翼上采用脉冲DBD激励也取得了明显控制效果；文献[4]在Λ=55°尖前缘三角翼上采用前缘非定常DBD激励取得了控制效果。然而，进一步增大后掠角后，文献[4,32]中在Λ=60°和Λ=75°三角翼的前缘激励没有取得明显的控制效果。文献[28]虽在Λ=60° 三角翼上取得效果，但是雷诺数太低，针对的是微型飞行器。

根据文献[32-33]的结果，总结了NS-DBD激励对30°、47°、60°后掠角三角翼前缘涡控制的测力试验结果，图7给出30 m/s下最大升力系数提高率随后掠角的变化。

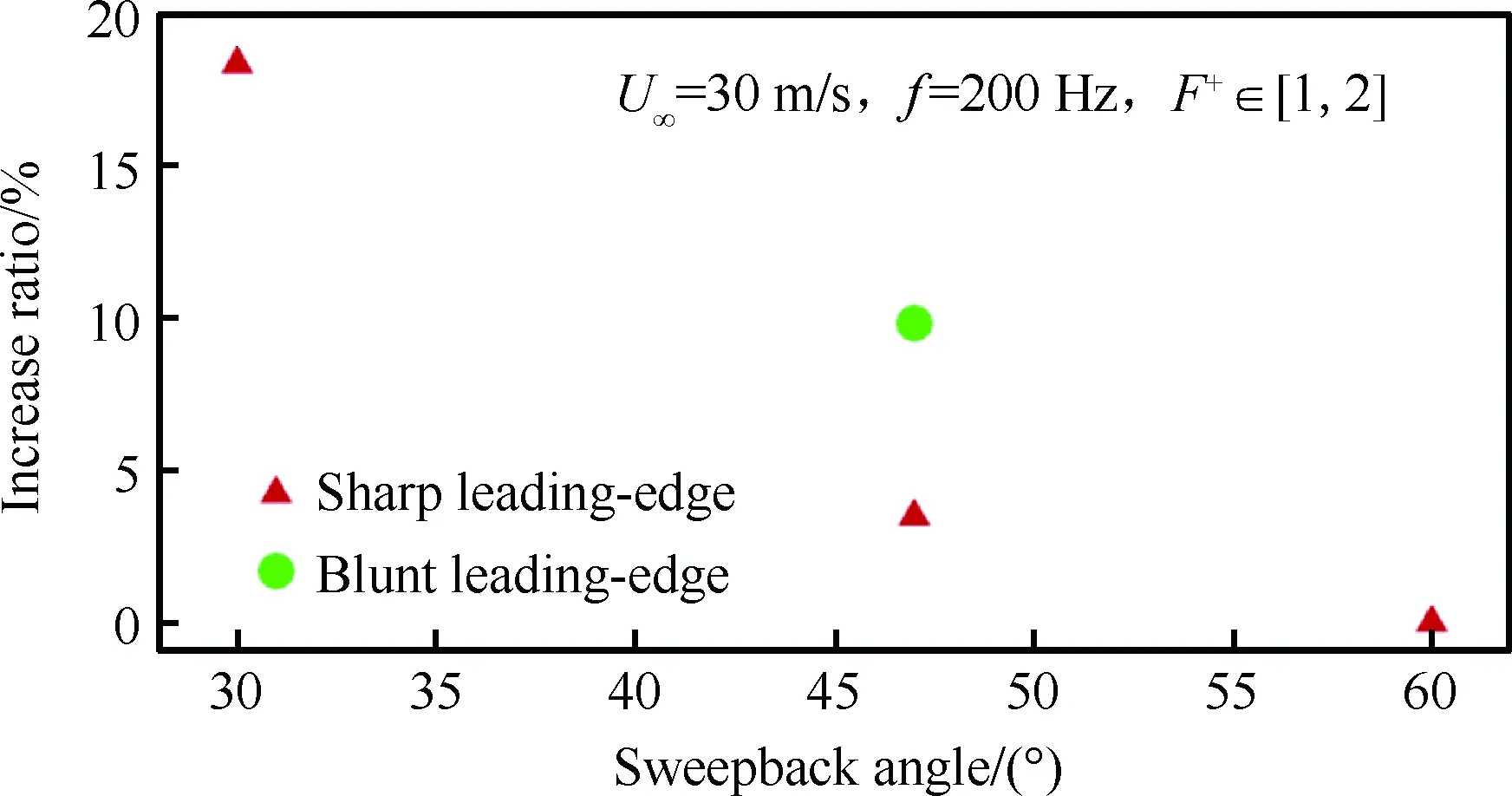
图7 不同后掠角最大升力系数提高率[32-33]Fig.7 Increase rate of maximum lift coefficient at different swept angles[32-33]

图7表明，对于前缘激励，其控制效果随后掠角的增大而减弱，对于大后掠角机翼无控制效果。后掠角的增大不利于前缘非定常激励的流动控制。结合图5，对大后掠角三角翼的涡控制，适合采用上翼面顺涡轴方向加速的激励布局方式。

对于机翼前缘非定常扰动，机翼后掠角的影响在文献[48]中进行了讨论。图8为扰动产生后在不同后掠角机翼上的传播轨道线，由于来流速度沿机翼前缘可分解为展向分速Ut和法向分速Un。不同后掠角下两分速度相对值不同，使得扰动传播轨道线对后掠角依赖较大。当后掠角较大时，展向速度分量较大，前缘扰动很快被吹向尾迹区。

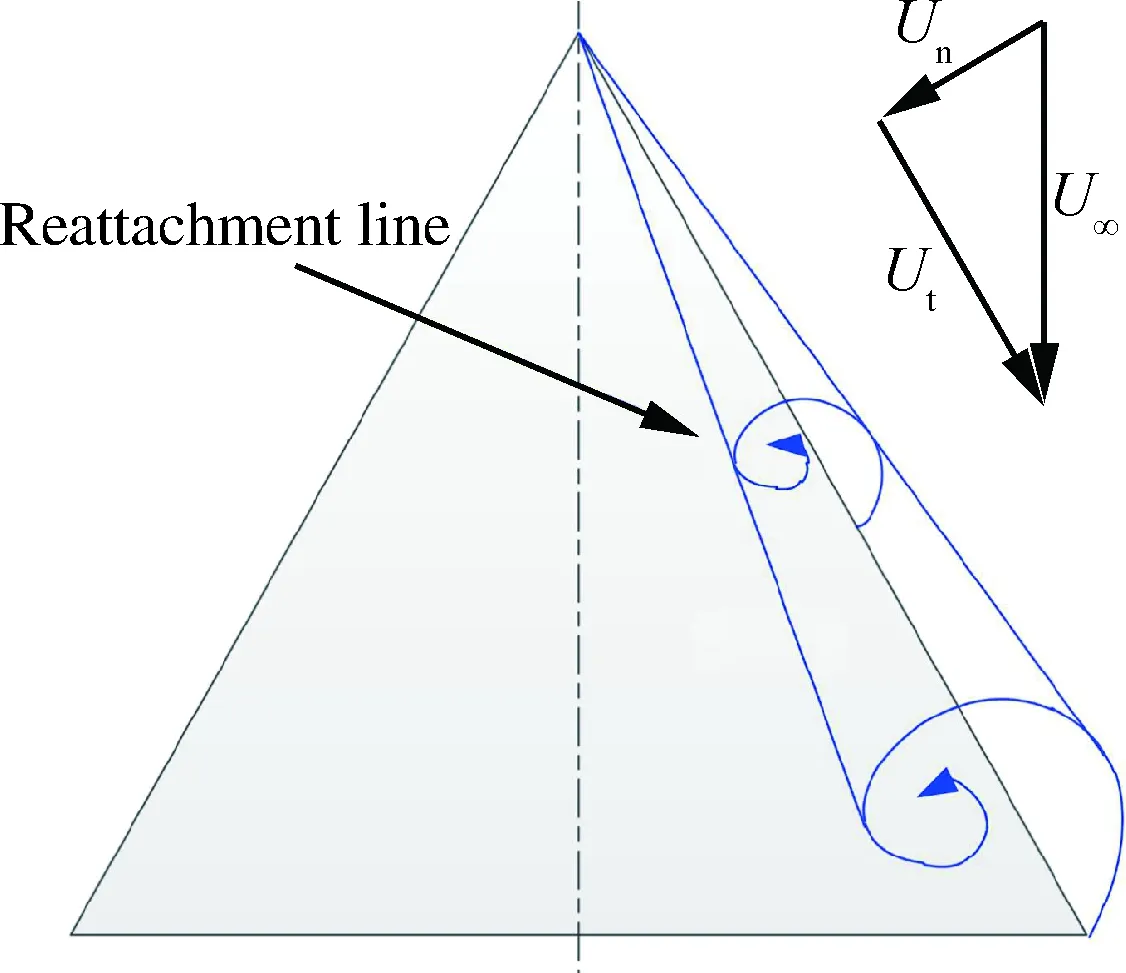
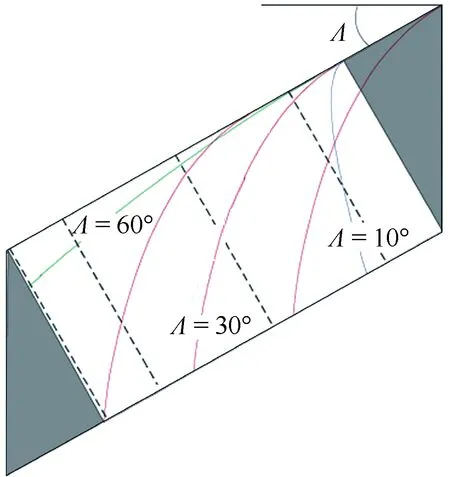
图8 三角翼前缘来流速度分解示意图和前缘扰动在不同后掠角机翼上的传播轨道[48]Fig.8 Diagram of velocity decomposition at leading-edge of delta wings and propagation trajectory of leading-edge excitation over different swept wings

5.2.2 前缘截面形状

研究已知，前缘截面形状对三角翼前缘涡特性的影响较大[49]，尤其影响附着线的位置[49]和升力系数[50]。这意味着前缘截面形状也会影响流动控制效果。作者所在实验室对两种前缘形状三角翼进行前缘涡控制试验，试验中机翼前缘截面形状如图9所示。

对于钝前缘三角翼，前缘激励可以取得明显的效果[33]；然而，将机翼更换成同样面积和后掠角的尖前缘三角翼时，前缘激励取得的控制效果大为减弱[32]，风洞测力试验结果如图10所示。实际中的飞行器前缘往往为钝前缘，因此研究钝前缘机翼的流动控制更有意义。

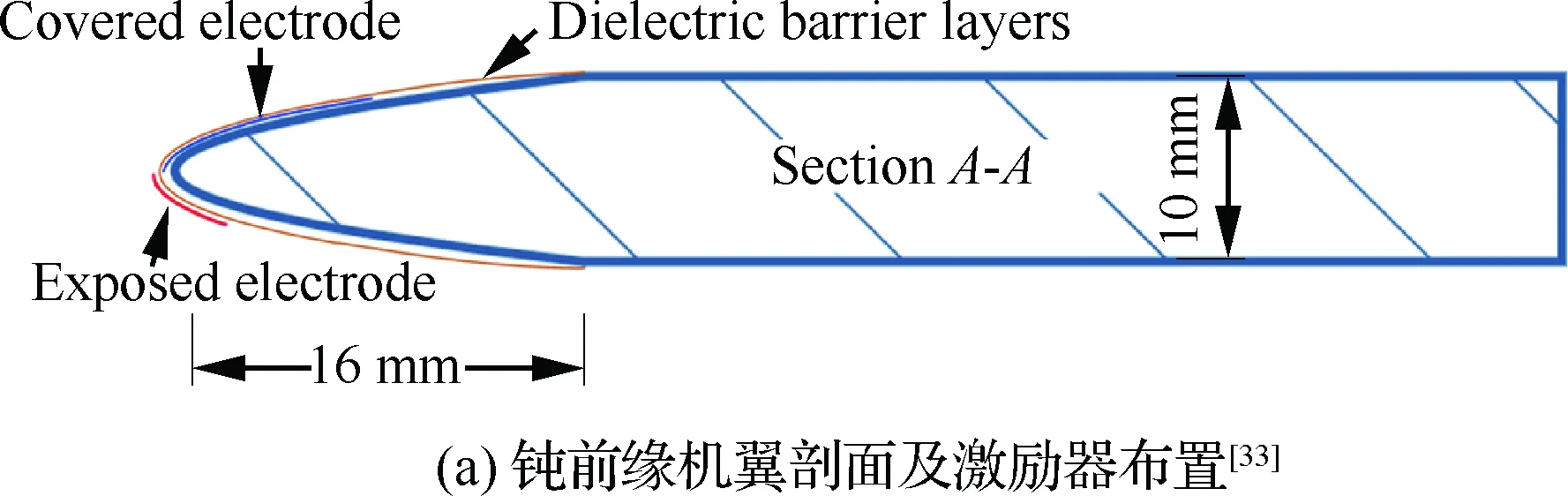
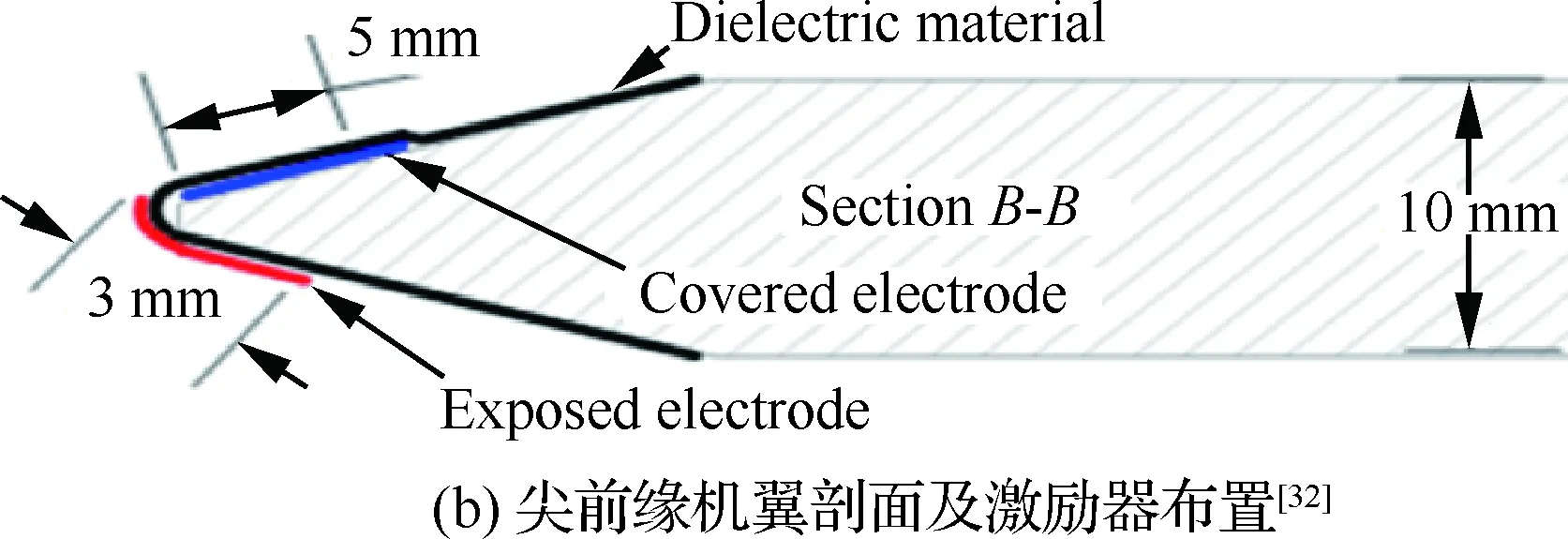
图9 两种不同的三角翼前缘截面Fig.9 Two different leading-edge cross-sections of delta wings

文献[49,51]通过天平测力、PIV(Particle Image Velocimetry)、油流试验研究了不同前缘形状对50°后掠角三角翼空气动力特性的影响。发现前缘半径对前缘涡的位置、尺寸、强度影响较大，同时对涡破裂点也有明显影响，如图11所示[49](图中ym-ymle为距前缘的展向位置)。

通过比较发现，尖前缘和钝前缘在前缘涡结构上有所不同，尖前缘涡结构稍大，涡核位置和附着线也靠机翼内侧。为解释NS-DBD控制效果的不同，通过观察，对图11中的前缘分离线近似拟合，发现不同前缘形状处的分离线的角度不同，尖前缘处的分离角最大，半圆形前缘处的分离角最小。在大迎角下，尖前缘相对应的分离角会更大，使得气流附着难度加大，等离子体流动控制的难度随之加大。

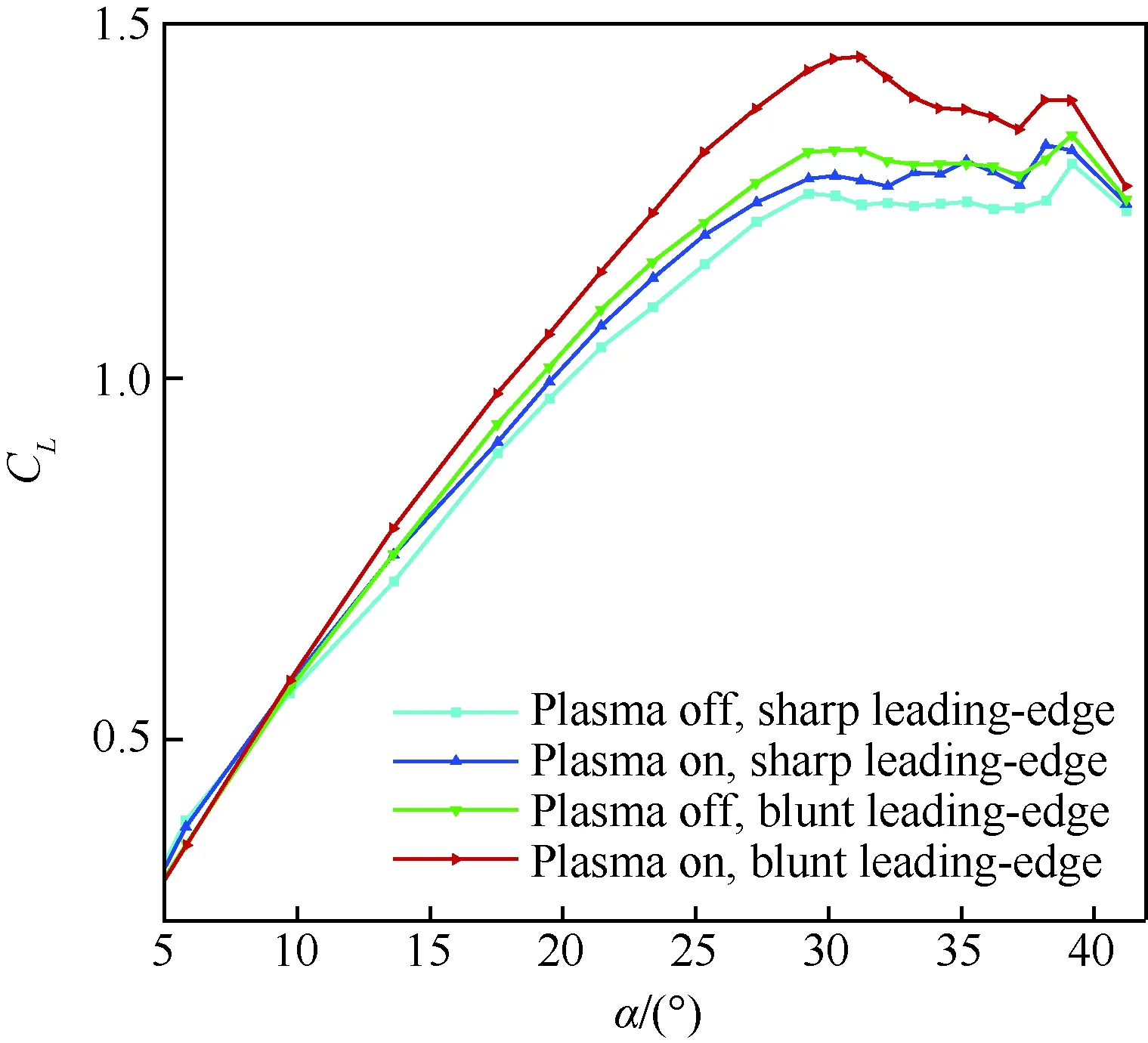
图10 两种不同前缘截面的三角翼激励前后的升力系数(U∞=30 m/s, F+=1.9)[32-33]Fig.10 Lift coefficients of delta wings with two different leading-edge cross-sections with plasma on and off(U∞=30 m/s, F+=1.9)[32-33]

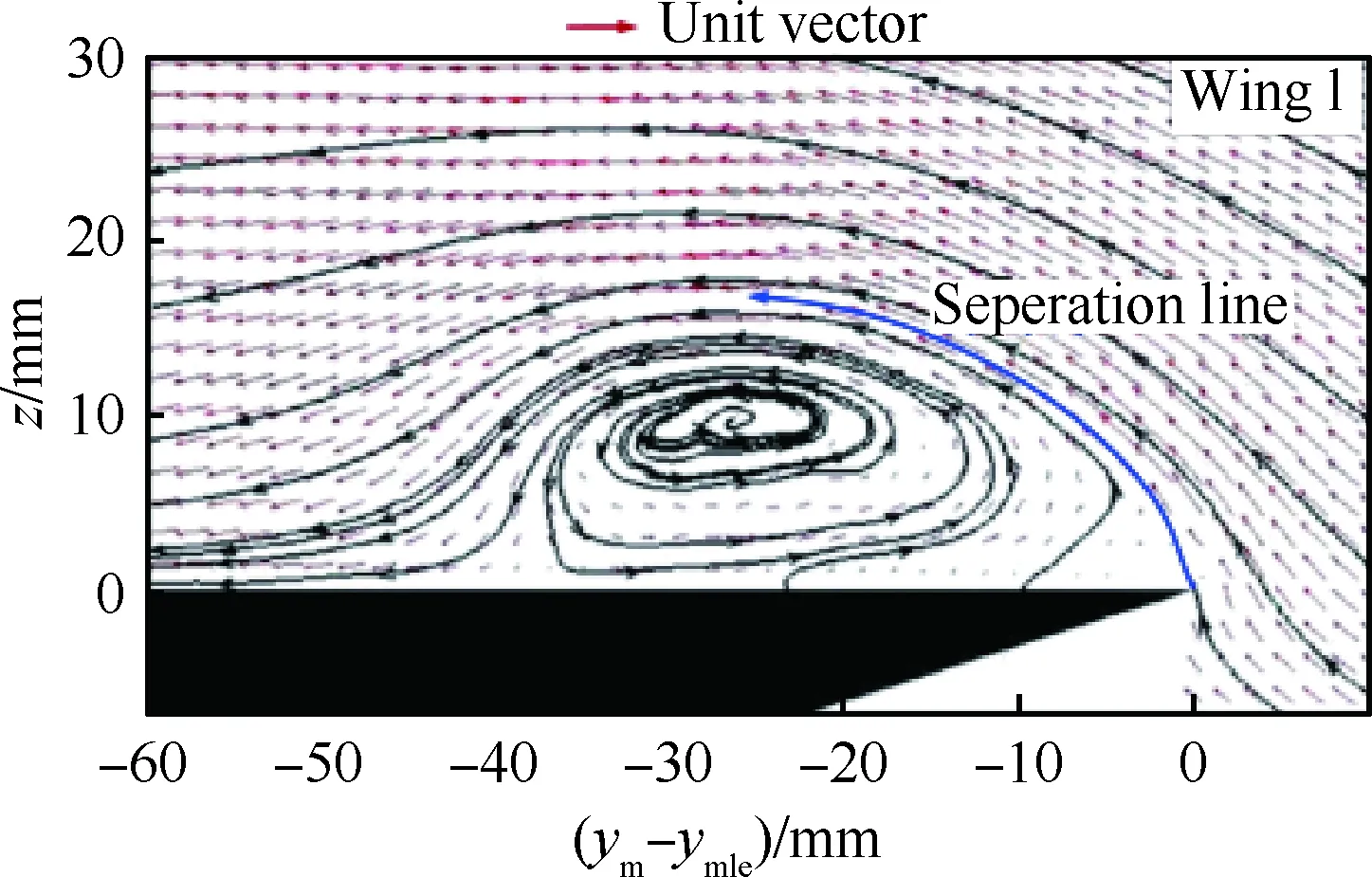
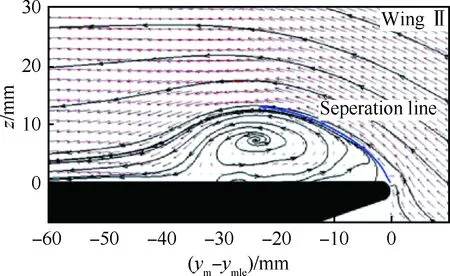
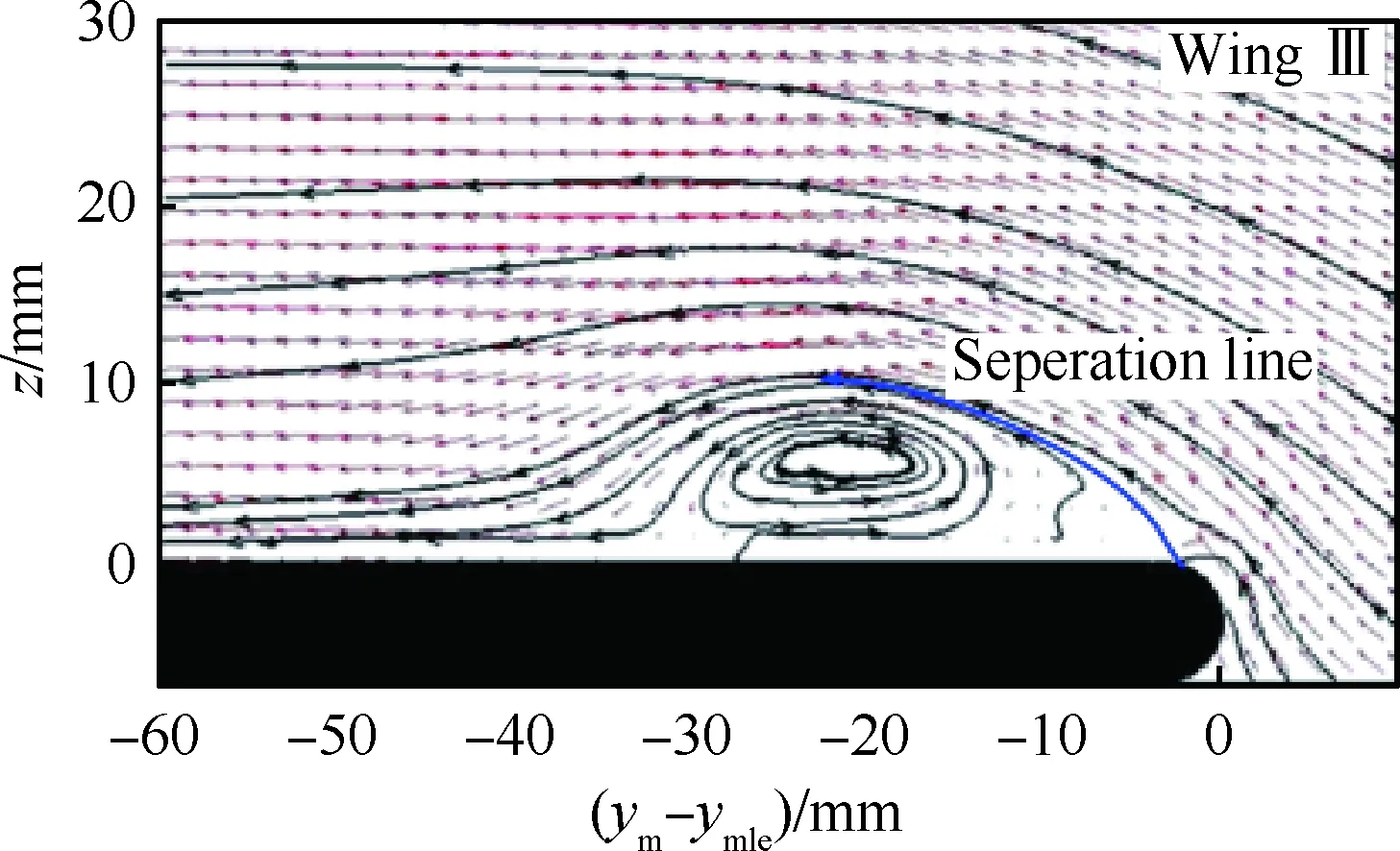
图11 翼面上60%弦长处截面速度场分布(α=15°)[49]Fig.11 Distribution of velocity flow field of section at 60% chord length over wing surface (α=15°)[49]

5.3 激励参数的影响

对于非定常DBD激励，激励参数主要有脉冲激励频率、激励电压。作者所在单位系统研究了NS-DBD激励电压和频率对三角翼前缘涡控制的影响。这里结合国际上研究结果，分析激励参数的影响规律。

5.3.1 脉冲激励频率

在前缘激励下，脉冲激励频率对结果的影响至关重要。图6给出了脉冲化的AC-DBD激励在不同调制频率下引起的升力系数增量，在低雷诺数下最佳激励频率F+=1，在较高雷诺数Re=75 000下，最佳激励频率F+在1～2范围内。这一最佳激励频率的范围与其他非定常激励方式(比如吹气、合成射流)是一致的[2,3]。

同时，文献[32-34]采用NS-DBD激励在三角翼前缘激励，所探测的最佳激励频率F+在1～2范围内。

研究认为，适当频率的非定常扰动可激发前缘剪切层K-H不稳定性，促进分离剪切层附体[2-3]。作者所在实验室，使用μs-DBD激励进行三角翼前缘涡控制研究，通过锁相PIV技术测得翼面上43.1%弦长处的流场[16]。在一个激励周期内，选择等时间间隔的4个相位进行测量。图12 给出了激励频率F+=2时的相平均速度场(图中T172是激励频率为172 Hz时的激励周期)。可以看出，激励施加后可在前缘剪切层处诱导产生一个新的旋涡结构，这里称之为诱导涡。诱导涡将剪切层外侧的主流卷入分离区，同时沿分离剪切层运动，最后与主涡合并。同时可以看到，该频率激励下翼根处的流动是附体的。

图12 PIV所测截面上4个相位的平均速度场(α=28°,Re=4.5×105,F+=2,T172=1/172 s, Vp-p=13.5 kV)Fig.12 Average velocity field of four vectors measured via PIV(α=28°, Re=4.5×105, F+=2, T172=1/172 s，Vp-p=13.5 kV)

μs-DBD激励对前缘分离涡的作用类似于非定常AC-DBD。文献[35]认为周期性诱导出现的小尺度涡沿剪切层运动，使得前缘涡结构得到重整，这与文献[4]认为的机理有所不同。文献[4]认为每次激励可诱导产生一个附着的前缘涡结构，逐渐发展成为一个大涡，取代原来的分离涡，直至发展成为一个分离的前缘涡；这样前缘涡周期性地诱导、发展、分离，维持了上翼面的涡升力。文献[4,35]中采用的均是非定常AC-DBD激励，PIV测试结果虽有不同，然而存在一个共性，就是激励在前缘涡产生处诱导出新的旋涡，将主流高能流动引入分离区；二者的区别可能是相对来流能量，激励的相对强度不同，强度高的扰动诱导附体的旋涡，强度低的扰动诱导沿前缘涡运动的小涡。

在激励频率F+=4时，在翼根处已经看不到明显附着的前缘涡结构，如图13所示(图中T345是激励频率为345 Hz时的激励周期)。这表明当激励频率超过一定的阈值时，将很难维持分离剪切层的附体，因为高频的激励使得分离剪切层分割为多段。与图12中F+=2时的流场相比，激励频率主要决定了剪切层上共存流向涡的数量；激励频率越大，共存流向涡越多。

图13 PIV所测截面上4个相位的平均速度场(α=28°，Re=4.5×105,F+=4，T345=1/345 s，Vp-p=13.5 kV)Fig.13 Average velocity field of four vectors measured via PIV(α=28°, Re=4.5×105， F+=4, T345=1/345 s， Vp-p=13.5 kV)

5.3.2 激励电压

DBD等离子体激励引起扰动的强度受激励电压影响最大，电压决定了注入流场能量的多少。当来流速度一定时，激励电压越大，激励引起扰动的相对强度增大，从而直接影响了控制效果。

对于NS-DBD激励，文献[52]观测到单位长度激励器放电能量与激励器长度无关，随电压近似呈指数增长。高的激励电压意味着较多能量注入流场。图14给出了在最佳频率下升力系数随激励电压的变化[16,33]，随着激励电压增大，其效果越好。电压升高到一定程度，增幅已经不明显,这暗示着可能与二维翼型一样，存在一个阈值电压，超过阈值电压，控制效果不再有明显改善。

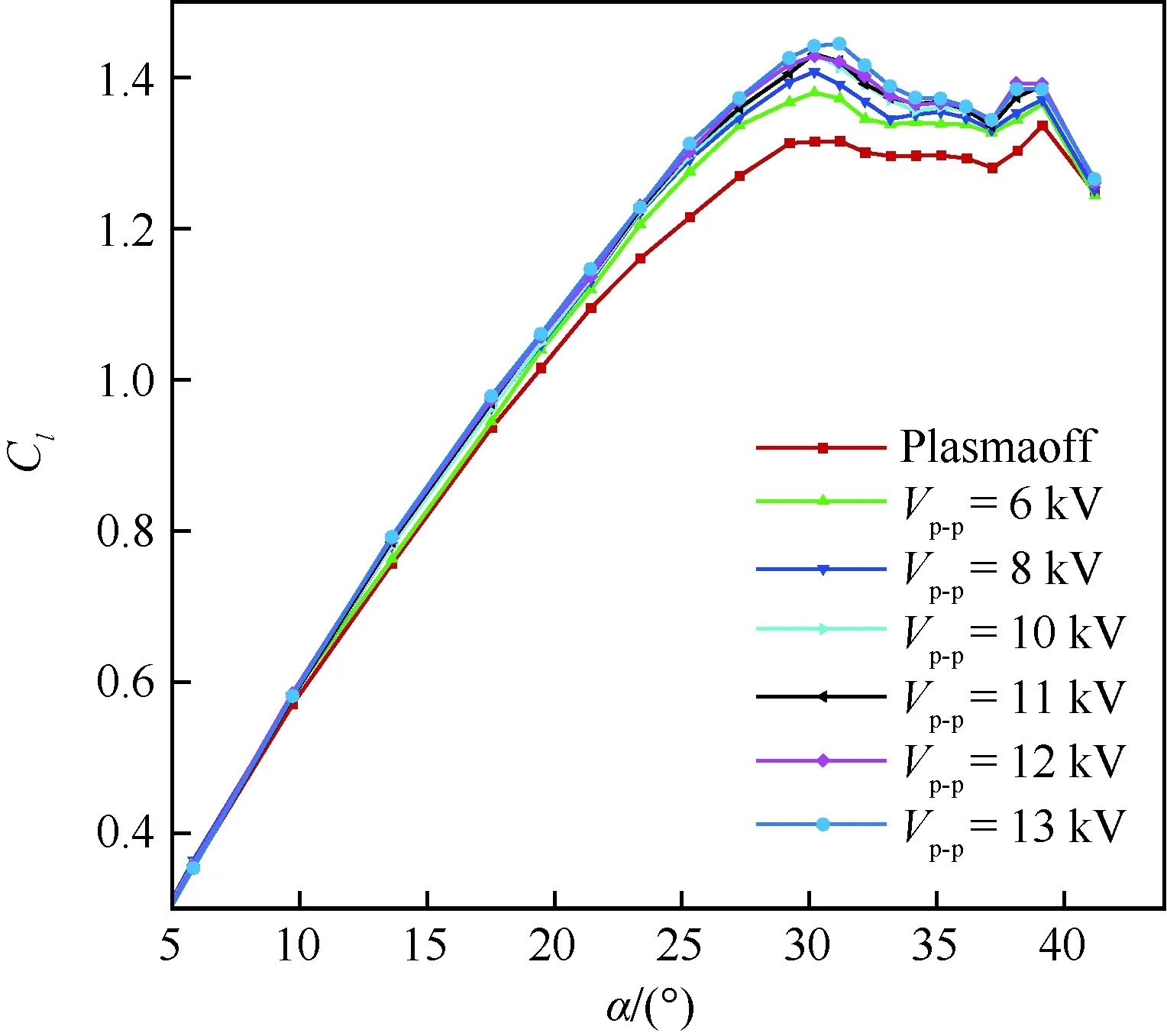
图14 NS-DBD激励前后三角翼的升力系数[16,33]Fig.14 Lift coefficients of delta wings before and after NS-DBD plasma actuation[16,33]

同时文献[4]中将非定常模式的AC-DBD激励施加在55°后掠角三角翼前缘，如图15所示。随电压的增大，大迎角下的法向力系数(CN)增大较多；同时在Vp-p=12.9 kV以后差别不大，这似乎也表明存在一个阈值电压。

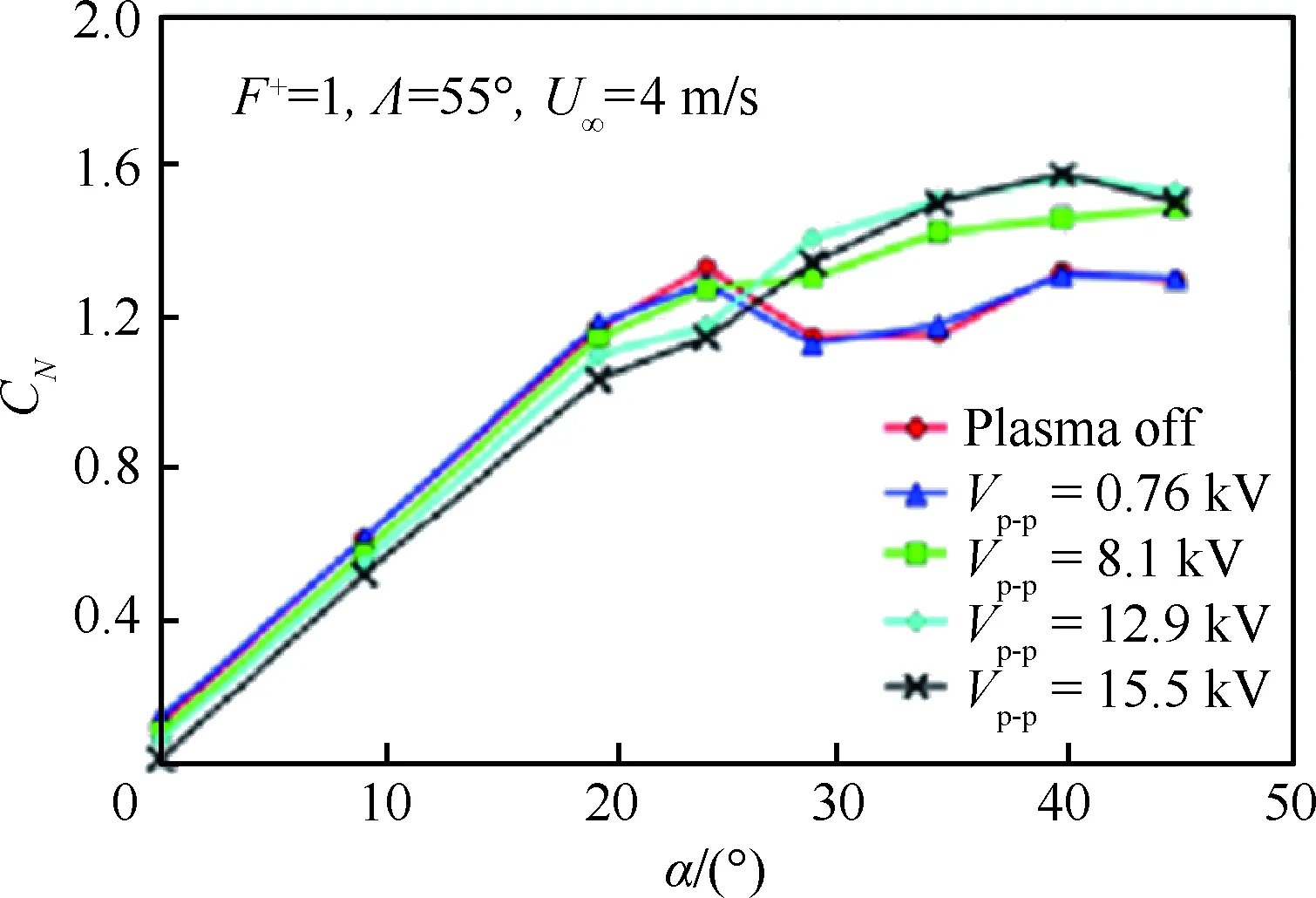
图15 前缘非定常AC-DBD激励引起的法向力系数变化[4]Fig.15 Variation of normal force coefficients caused by unsteady AC-DBD actuation on leading-edge [4]

对于非定常AC-DBD激励，占空比也是一个值得研究的重要参数。文献[28]认为最佳的占空比为10%；然而对于kHz量级的μs-DBD和NS-DBD激励，单脉冲的脉宽相对很小，不存在占空比的影响。

6 总结与展望

本文介绍了流动控制中常用的DBD等离子体激励方式和基本原理，总结了其用于三角翼前缘涡控制研究现状，并从来流条件、三角翼几何构型、激励参数等方面分析了影响三角翼前缘涡控制的主要因素。

定常模式的AC-DBD激励可被认为是直接的动量注入，最佳的位置会在不同弦向处诱导顺涡轴方向的附面层加速；然而，AC-DBD激励诱导的动量严格受制于放电区域内离子浓度，使得AC-DBD激励强度相对不足，从而限制了其在较高速度下的应用，类似问题在二维翼型绕流控制中也存在。目前其在三角翼涡控制研究中，来流速度不超过30 m/s。

非定常模式的DBD激励主要有非定常AC-DBD、μs-DBD和NS-DBD，可被认为是通过间接控制方式将主流高能流引入分离区，最佳的位置是在机翼前缘分离剪切层形成处。其中NS-DBD激励可在Ma=0.4，Re=2.03×106来流下，对35°后掠角飞翼布局前缘涡有效控制[27]。在50 m/s 下对中等后掠角三角翼也有很好的控制效果[34]。然而，非定常模式的DBD激励对细长三角翼流动控制效果微弱。

总之，等离子体流动控制作为一种新型的流动控制技术，其在三角翼绕流控制上的研究还处于初步研究阶段，主要针对前缘涡的控制。未来在以下几个方面还需进一步深入研究。

1) 开展精细化的流场显示试验。目前DBD激励控制三角翼绕流的流场显示主要通过烟流和二维PIV技术，由于三角翼绕流具有很强的三维特性，伴随着DBD激励与流场的复杂耦合作用，因此需要探索采用时空分辨率高的三维流场显示手段，比如三维PIV技术。

2) 开展相应的高精度数值仿真。目前DBD激励用于三角翼涡控制研究主要以试验为主，相对应的仿真研究亟需开展，与流动显示互为补充，获得流场的动态演化特性，揭示流动控制机理。

3) 开展对应飞行条件下的风洞试验。NS-DBD激励在二维翼型上的可控速度较高，控制能力较强；其用于三角翼的绕流控制，还没有高速和高雷诺数下的试验验证，对应飞行条件下的风洞试验还有待开展。

4) 进一步探究不同构型三角翼绕流控制的最佳激励位置。鉴于细长三角翼和非细长三角翼绕流特点的不同，需要有针对性地开展流动控制研究，进一步探索不同构型三角翼上最佳的激励位置。前缘非定常DBD激励对细长三角翼没有取得明显控制效果的原因有待进一步研究。

5) 进一步明确研究的应用背景，开展相对应的试验研究。作者认为其可能的应用方向有：控制前缘涡引起的非对称流动，改善前缘涡稳定性，减缓翼尖抖振，用于飞行控制。