前缘和转轴影响翼摇滚特性的数值模拟*

杨小亮，黄世林，杨 起，柴振霞，孙喜万，刘 伟

(1. 国防科技大学 空天科学学院， 湖南 长沙 410073； 2. 中国人民解放军93108部队， 黑龙江 齐齐哈尔 161007)

三角翼因结构强度高、可提供非线性涡升力等优点，是现代战斗机主要采用的机翼构型，其气动特性受到了学界的普遍关注，尤其是其动态特性密切关系到现代战斗机大攻角机动飞行的安全[1]。大攻角条件下，三角翼会产生大幅度自维持的翼摇滚现象。虽然早在20世纪中叶，人们就观察到了翼摇滚现象，但由于其复杂的非线性气动特性，直到20世纪80年代才陆续出现对三角翼摇滚现象较为系统的试验研究[2-5]，而耦合求解N-S方程和Euler刚体动力学方程[6-10]完成三角翼摇滚现象的数值模拟则是二十多年来才开始的事情。

准确捕捉位于三角翼背风面的非线性集中涡是数值模拟三角翼绕流时必须解决的问题。近年来，大量文献在模拟、分析及控制三角翼上涡流特性方面不遗余力[11-15]，进展卓有成效[16]，而数值模拟涡流主导的三角翼摇滚现象则主要集中在捕捉摇滚现象的定性研究。三角翼上集中涡形成和发展具有强非线性，故对三角翼构型及影响因素极为敏感[17]，造成了数值模拟与实验之间、实验与实验之间往往存在明显的分歧[5]。提升数值模拟和风洞实验反映翼摇滚现象物理本质的水平，减小数值模拟和实验差距，必须研究翼摇滚特性的影响因素。前缘构型和滚转轴安装位置是实验研究必须陈述的关键细节，且文献[4-5]表明不同的处理可导致摇滚特性显著不同。阎超等[18]研究了前缘形状对三角翼上涡流特性的影响,但对摇滚特性影响的研究则相对较少。本文耦合求解N-S方程和刚体动力学方程，针对80°后掠三角翼研究前缘构型和转轴安装位置影响三角翼摇滚特性的程度和规律。

1 模型及计算方法

1.1 三角翼模型及网格

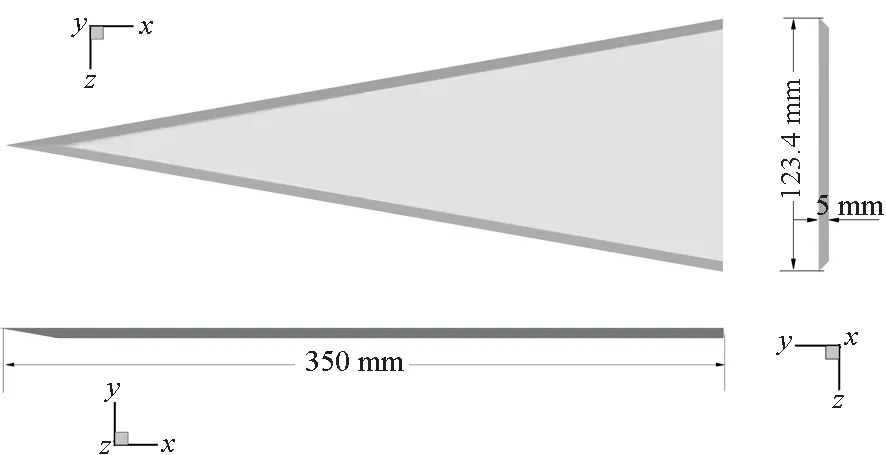
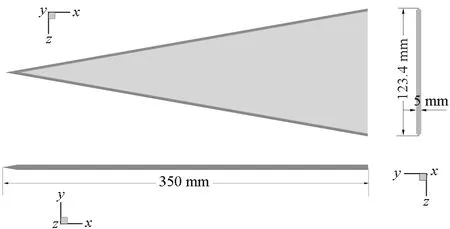
研究采用80°后掠尖前缘平板三角翼模型，前缘分别采用下削尖、双面削尖、上削尖三种方式，削尖角均为45°，尾缘不做削尖处理，垂直翼面，如图1所示。为研究滚转轴对细长三角翼摇滚特性的影响，基于下削尖前缘三角翼分别研究了滚转轴安装在四种不同位置时的摇滚特性，如图2所示，滚转轴位置分别安装在下翼面下方5 mm处(记为Axel_DD)、下翼面上(记为Axel_D)、上翼面上(记为Axel_U)、上翼面上方5 mm处(记为Axel_UU)，四种安装位置的滚转轴均位于三角翼体对称面上。网格生成采用OH型拓扑结构，周向O型、其余方向H型，以平衡描述精度和网格规模[19]。计算网格如图3所示，网格上游边界距离三角翼顶点2.5倍根弦长，周向边界距离体轴2.5倍根弦长，下游边界距离三角翼尾缘5倍根弦长。网格数为112×226×50(流向×周向×法向)，翼尖、尾缘及翼前缘附近流动较为复杂，局部适当加密。

(a) 下削尖前缘(a) Down beveled leading edge

(b) 双面削尖前缘(b) Double beveled leading edge

(c) 上削尖前缘(c) Up beveled leading edge图1 三种不同前缘形状的80°后掠三角翼模型Fig.1 Three 80° swept delta wing model with different leading edge configuration

(a) 滚转轴位于下翼面下方(Axel_DD)(a) Roll-axis under the lower wing surface(Axel_DD)

(b) 滚转轴位于下翼面(Axel_D)(b) Roll-axis on the lower wing surface(Axel_D)

(c) 滚转轴位于上翼面(Axel_U)(c) Roll-axis on the upper wing surface(Axel_U)

(d)滚转轴位于上翼面上方(Axel_UU)(d) Roll-axis above the upper wing surface(Axel_UU)图2 四种不同滚转轴位置示意图Fig.2 Schema of four roll-axis installation of delta wing

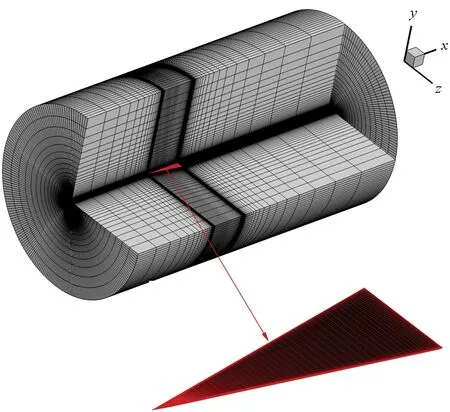
图3 80°后掠三角翼网格分布Fig.3 Grid distribution of the 80° swept delta wing

1.2 数值方法

采用非定常N-S方程组和滚转动力学方程描述三角翼单自由度摇滚运动[20]，贴体坐标系(t,ξ,η,ζ)下的方程写为：

(1)

基于结构网格的有限体积法，采用Roe格式和含双时间步的LU-SGS方法离散非定常N-S方程组。滚转动力学方程采用时间二阶精度的单边差分离散，得到时间二阶精度的滚转差分方程：

(2)

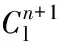
非定常N-S方程组和滚转动力学方程的耦合求解采用松耦合模式，即由滚转动力学方程提供三角翼n+1时刻的位置，再由非定常N-S方程组计算n+1时刻的滚转力矩系数。

远场采用无反射边界条件，壁面边界取绝热壁，压力条件为∂p/∂n|wall=-ρawall·nwall，速度条件为无滑移条件，即V=Vwall。

1.3 验证与确认

本文的计算基于国防科技大学刘伟教授团队开发的飞行器动态特性研究程序(Aircraft Dynamic Characteristics Research Program, ADCRP)。该程序针对多块对接结构网格，求解三维非定常RANS方程，经过二十余年的发展，具备复杂飞行器流动/运动耦合的多自由度非定过程的数值模拟能力。该程序采用系列标模外形进行了系统的验证与确认计算，适用于三角翼等定、动姿态非定常问题的分析[20-21]，在多个型号项目中得到了应用。该程序具备模拟细长三角翼摇滚现象的研究能力。

2 前缘构型对摇滚特性的影响

考察前缘构型对细长三角翼摇滚特性的影响。计算时，给定来流马赫数Ma=0.2，基于根弦长度的雷诺数Re=0.4×106，无量纲滚转转动惯量Ixx=0.1，滚转轴与x轴重合且位于上翼面，不计轴承阻尼。统一给定10°的初始滚转角，研究不同前缘三角翼的滚转响应，分别对分岔攻角和摇滚振荡的振幅进行讨论。

2.1 前缘形状对分岔攻角的影响

文献[22]指出，三角翼攻角α变化会导致其横向稳定性发生Hopf分岔，存在攻角的临界值，攻角小于该值，三角翼横向动态稳定，大于该值，三角翼发生横向失稳，形成大幅度自维持的极限环振荡，该临界值称为分岔攻角。

对分岔攻角的数值模拟结果如图4所示，显示了下削尖、双面削尖、上削尖三种前缘构型的三角翼不同攻角下的滚转角时间历程。按照文献描述，易于判断下削尖前缘三角翼分岔攻角约为22.4°，双面削尖前缘三角翼分岔攻角约为16.9°，上削尖前缘三角翼分岔攻角约为15.5°。其中：下削尖前缘三角翼能够在较大的攻角范围保持滚转稳定性，分岔攻角最大；上削尖前缘三角翼分岔攻角最小，即最容易发生横向失稳；双面削尖前缘的三角翼横向稳定性介于二者之间。

(a) 下削尖前缘(a) Down beveled leading edge

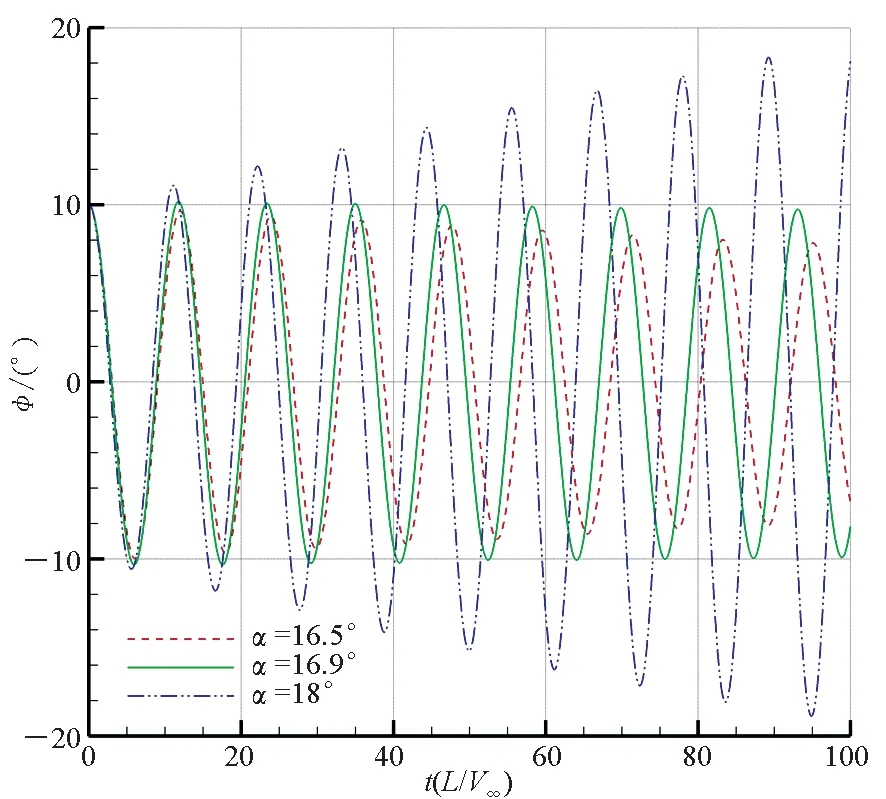
(b) 双面削尖前缘(b) Double beveled leading edge

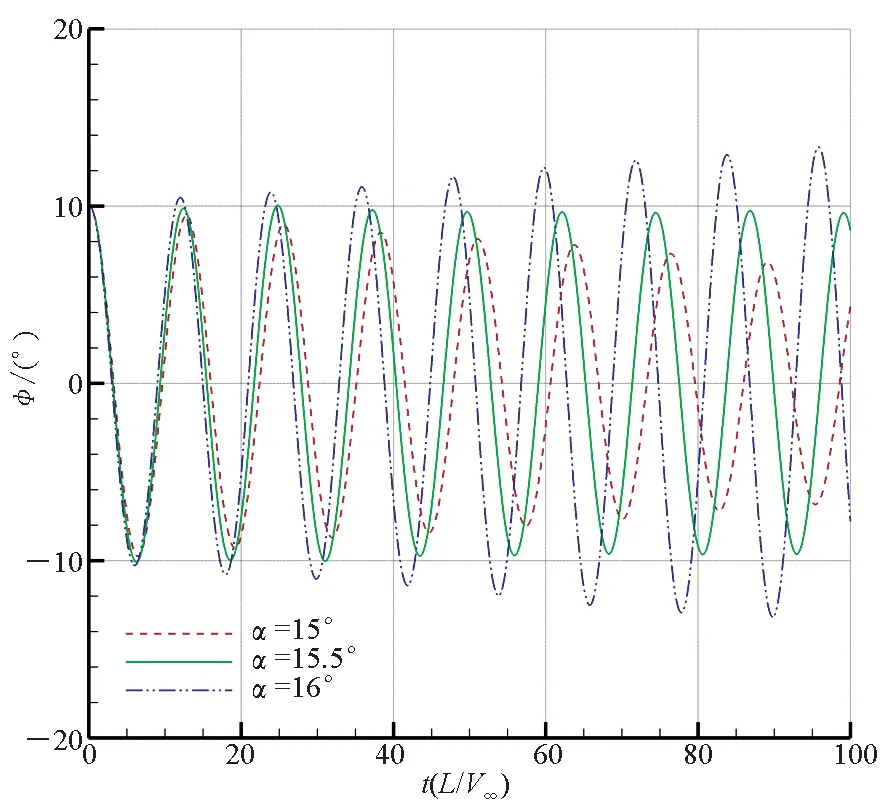
(c) 上削尖前缘(c) Up beveled leading edge图4 不同前缘形状三角翼的滚转角时间历程Fig.4 Time history of roll angle of delta wing with different leading edge

为进一步理解前缘构型对三角翼动态特性的影响，基于强迫简谐分析法计算三角翼滚转稳定性参数，如表1和表2所示。稳定性参数为负则表示具有稳定性，为正则表示不稳定。由表1可知：不同前缘构型的三角翼，在所研究的攻角范围内都是静稳定的，整体而言，静稳定性相当。由表2可知：随着攻角增大，滚转阻尼导数由负变正，表明从滚转动稳定变为滚转动不稳定，从动态稳定性的角度说明了三角翼滚转方向发生Hopf分岔的这一现象。其中，下削尖三角翼在22.4°、双面削尖三角翼在16.9°、上削尖三角翼在15.5°时，滚转阻尼导数的绝对值显著小于其他角度的绝对值，这表明此时三角翼几乎处于无阻尼状态，正好对应三角翼在跨过该攻角时的滚转稳定性性态的变化，分岔攻角在以上角度附近。

表1 三角翼滚转静稳定性导数

表2 三角翼滚转阻尼导数

2.2 前缘形状对振幅特性的影响

上一节的研究表明，攻角大于分岔攻角以后，均会发生横向失稳，形成大幅度自维持极限环形式的摇滚现象。为进一步考察不同前缘构型的三角翼横向失稳以后的动态特性，选取25°和30°攻角，给定0°初始滚转角，研究前缘形状对三角翼振幅特性的影响，结果如图5所示。

25°攻角时，如图5(a)所示，三种前缘构型的三角翼均形成了极限环形式的等幅振荡，下削尖前缘三角翼的振幅约为19.2°，双面削尖前缘三角翼的振幅约为65.2°，上削尖前缘三角翼的振幅约为75.6°。其中，下削尖三角翼振幅最小，双面削尖三角翼次之，上削尖三角翼的振幅最大，对比表2数据，三种前缘构型的三角翼的滚转阻尼导数均为正，从数值上而言，下削尖三角翼最小，双面削尖三角翼次之，上削尖三角翼最大，三角翼自激滚转振荡的表现与动态稳定性参数预示的规律一致。

30°攻角时，如图5(b)所示，三种机翼均最终形成了极限环形式的等幅振荡，但双面削尖和上削尖前缘的三角翼在发生翻转后绕滚转轴进行滚转振荡。其中，双面削尖前缘三角翼摇滚振幅约为49.8°，上削尖前缘三角翼摇滚振幅约为31.4°，下削尖前缘三角翼未发生翻转，其振幅约为37.1°。

理论上讲，双面削尖前缘三角翼，上下对称，翻转后与自身同构，上削尖前缘三角翼与下削尖前缘三角翼在结构上相同，仅与来流在空间的相对位置不同。上削尖前缘三角翼翻转后，空间位置与下削尖前缘三角翼相同。但由图5(b)观察到的结果，上削尖前缘三角翼翻转后的振幅(31.4°)与下削尖前缘三角翼的振幅(37.1°)并不相同。经分析，主要由于翻转后滚转轴位置不相同，对于双面削尖的三角翼同样存在该问题，需要进一步分析。

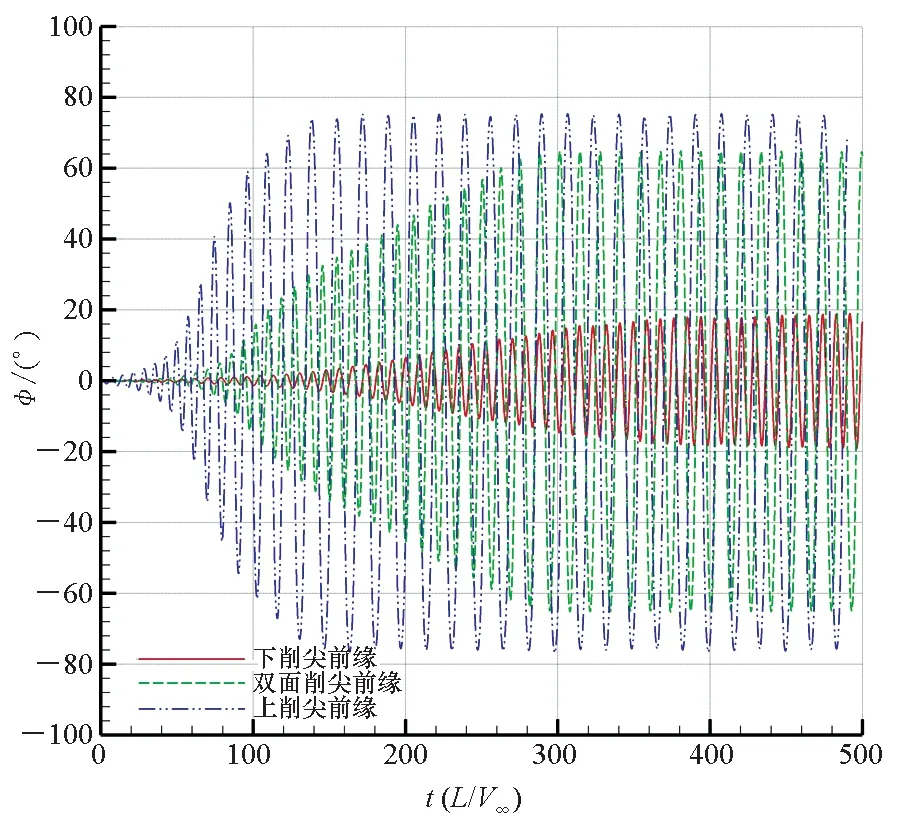
(a) α=25°

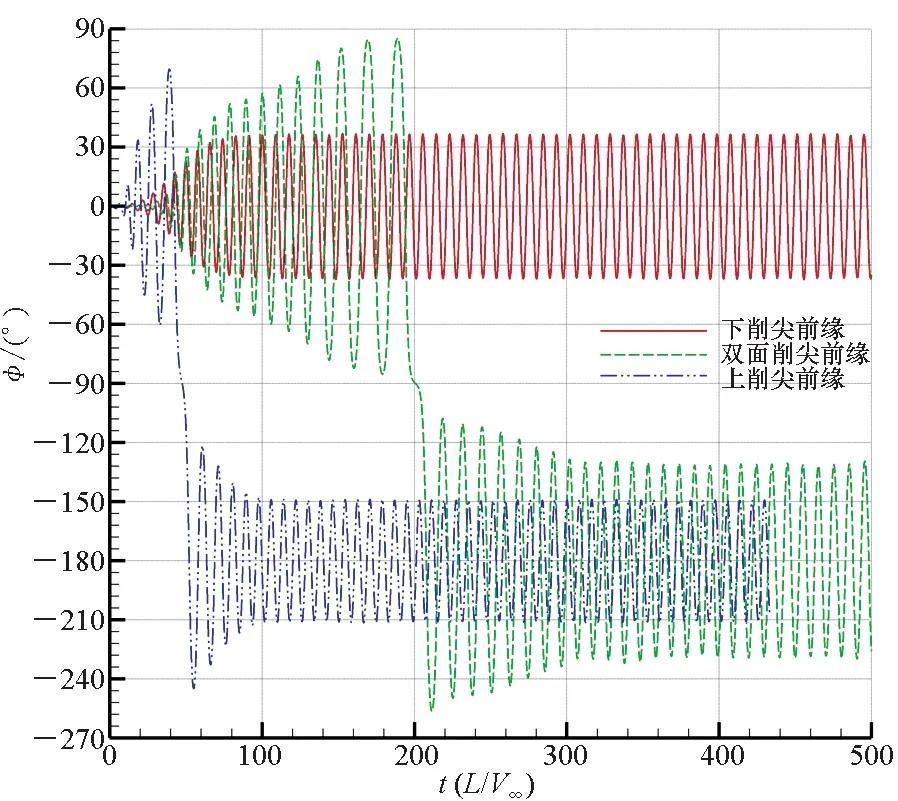
(b) α=30° 图5 不同前缘构型三角翼在大攻角下的摇滚特性Fig.5 Wing rock characteristics of delta wing with different leading edge in high angle of attack

3 滚转轴位置对摇滚特性的影响

基于对三角翼摇滚现象的理解，进一步考察滚转轴位置对细长三角翼摇滚特性的影响。计算时，给定来流马赫数Ma=0.2，基于根弦长度的雷诺数Re=0.4×106，无量纲滚转转动惯量Ixx=0.1，统一指定10°的初始滚转角，不计轴承阻尼。选取下削尖三角翼，指定不同滚转轴位置，如图2所示，研究滚转轴位置对摇滚特性的影响，分别对分岔攻角和摇滚振幅进行了讨论。

3.1 滚转轴位置对分岔攻角的影响

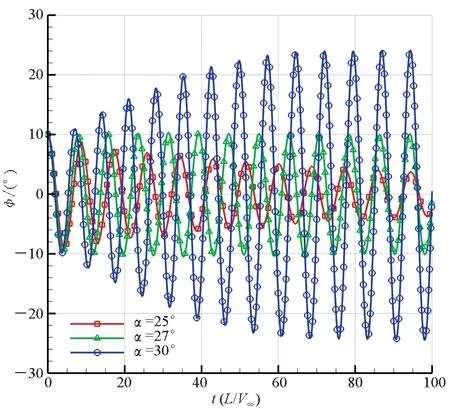
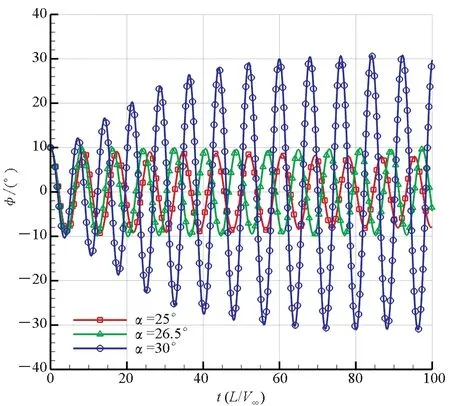
如图6(a)所示，滚转轴位于下翼面下方5 mm处时，三角翼从10°初始滚转角释放后，在25°攻角下摇滚振幅呈衰减状态，在30°攻角下摇滚振幅呈增大状态，而在27°攻角时摇滚振幅基本保持10°不变，说明滚转轴位于下翼面下方5 mm的三角翼的分岔攻角约为27°。由图6(b)～(d)易知，滚转轴位于下翼面的三角翼分岔攻角为26.5°，滚转轴位于上翼面的三角翼分岔攻角为22.4°，滚转轴位于上翼面上方5 mm处的三角翼的分岔攻角为17.4°。由此可见，随着滚转轴从下翼面下方5 mm处移动到上翼面上方5 mm处，三角翼的分岔攻角逐渐减小。可以得出结论，在所研究的滚转轴位置范围内，滚转轴位置越高，三角翼摇滚的分岔攻角越小，越易于横向失稳，反之亦然。

(a) 滚转轴位于下翼面以下(Axel_DD)(a) Roll-axis under the lower wing surface(Axel_DD)

(b) 滚转轴位于下翼面(Axel_D)(b) Roll-axis on the lower wing surface(Axel_D)

(c) 滚转轴位于上翼面(Axel_U)(c) Roll-axis on the upper wing surface(Axel_U)

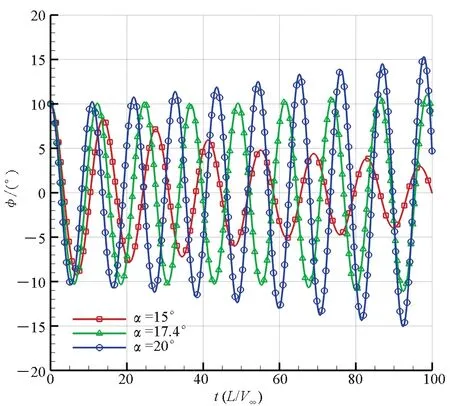
(d) 滚转轴位于上翼面以上(Axel_UU)(d) Roll-axis above the upper wing surface(Axel_UU)图6 不同滚转轴位置的三角翼滚转角时间历程曲线Fig.6 Roll angle time historical solution of delta wing installed at different roll-axes

3.2 滚转轴位置对振幅特性的影响

进一步研究滚转轴位置对三角翼振幅特性的影响，给定30°、40°、50°和60°攻角，模拟四种滚转轴位置的三角翼摇滚振幅特性，计算结果如图7所示。

从图7中可以看出，四种滚转轴位置下摇滚振幅随攻角变化的规律基本一致，30°攻角时，四种滚转轴位置的三角翼均形成了极限环自激摇滚，滚转轴位置越靠上振幅越大；40°攻角左右建立最大振幅，随着攻角进一步增大，由于受到涡破裂的影响，摇滚振幅随攻角增大而减小；当攻角增加到60°以后，四种滚转轴位置的三角翼均难以形成大幅度的摇滚振幅。

图7 摇滚振幅随攻角变化曲线Fig.7 Amplitude of roll varies with attack angle

4 结论

耦合求解三维非定常N-S方程和欧拉刚体动力学方程组，研究了前缘构型与滚转轴位置对80°后掠平板三角翼摇滚特性的影响，得到以下结论：

1)前缘削尖方式不改变三角翼横向动态稳定性的性态，但影响三角翼摇滚的分岔攻角和摇滚振幅；不同前缘构型三角翼的自激摇滚特性与动态稳定性参数表征的稳定性一致。

2)对于转轴位于上表面的三角翼，攻角25°时,前缘下削尖时摇滚振幅最小，上削尖时摇滚振幅最大；攻角30°时，双面削尖前缘和上削尖前缘的三角翼自激摇滚时发生了翻转，翻转后绕滚转轴等幅振荡，双面削尖前缘与上削尖前缘三角翼先翻转后再形成极限环形式的等幅振荡。

3)滚转轴的安装位置影响三角翼的摇滚特性，滚转轴位置越高，三角翼摇滚的分岔攻角越小，极限环滚转振荡的振幅越大，反之亦然。

三角翼摇滚现象研究多年依然是热点问题，对其产生和维持机理已有较多深刻的认识，但对敏感因素的分析还不足，旋涡等流动结构与飞行器之间作用的过程和机理等问题仍值得进一步的分析。