磁绝缘传输线阴极准直建模与仿真*
何德雨,呼义翔,曾江涛,杨 实,周亚伟,孙 江,尹佳辉,丛培天
(强脉冲辐射环境模拟与效应国家重点实验室 西北核技术研究所, 陕西 西安 710024)
由于真空磁绝缘传输线(Magnetically Insulated Transmission Line, MITL)能够实现超高电压梯度下的高功率脉冲的传输和汇聚,在目前已建或在建的国内外大型脉冲功率装置中得到了广泛的应用[1-7]。为获得超高功率指标,并受隔离驱动源和负载的设计需求等因素影响,MITL往往具有较长尺度,可达十余米,如美国圣地亚实验室的Hermes Ⅲ装置的MITL阴极总长达到18.7 m[8]。如果不采取矫直措施,如此长的悬臂支撑结构将会在末端产生数十毫米的挠度变形,造成整个MITL阴阳极无法实现有效对中,从而影响磁绝缘效果并会引起较高的电流损失。有文献提出采用电感支撑的方法保证阴阳极同轴度,但该方法的弊端是在原理上就会产生电流损失[9-10],并且即使末端的同轴度得到保障,中间段的挠度仍可能达到数毫米量级;此外,电感支撑的安装需要较大空间,在阴阳极间隙较小的场合中不能适用。如今,长距离磁绝缘传输的中心电极支撑定位问题已经成为超高功率脉冲传输的关键问题之一[11]。针对该问题,Hermes Ⅲ装置采用了基于倾斜垫片的阴极矫直策略,将阴极分节装配,并在节与节之间安装具有一定斜度的倾斜垫片,通过计算和调节倾斜垫片的相对步进转角,补偿重力引起的挠度变形,从而将整个阴极的直线度误差控制在阴阳极间隙的5%以内。这种基于倾斜垫片的准直策略是目前能够用于解决长悬臂结构挠度变形的最有效手段之一,但在现有文献中关于具体的建模和调节方法的介绍尚较粗浅。本文试图通过设计较小尺寸的MITL阴极筒,从理论上研究上述问题。
1 Mini-MITL阴极筒设计
1.1 设计目的和方法
Mini-MITL阴极筒是用于准直建模和调节原理验证的简化装置。在正式装置建设之前,有必要设计较小尺寸的MITL阴极筒进行实验验证。其一,正式装置的MITL阴极筒体量巨大,在前期论证阶段对准直方案进行实验验证和改进优化,可以有效降低工程风险,提高工程建设效率。其二,基于倾斜垫片的阴极准直方案涉及工程测量的技术范畴,与之相关的专业光学测量仪器操作复杂,需要通过实验制定可行的测量方案。其三,为了确保MITL阴极与阳极之间的准确对中,需要设计阴极筒整体的角度和位置机械调节方案,该方案同样需要前期的实验验证。为了达到验证的逼真性和有效性,在零件的基本结构设计上,Mini-MITL阴极与正式装置阴极几乎相同,但尺寸和同类件数量等存在差异。
为了使阴极末端在重力作用下的挠度达到数厘米量级,需要对阴极筒的外径、壁厚以及长度进行估算。从宏观上看,阴极筒由若干节外径呈阶梯式变化的薄壁圆筒组合而成。考虑长为l、在集度为q的均布载荷作用下的悬臂梁,其末端挠度的计算公式为[12]:
(1)

(2)
从上式可以看出,外径D越大,壁厚越小(d越大),则圆筒的悬臂末端挠度越小。外径D越大,相应的造价成本越高,但如果过小,又不利于装配操作;减小壁厚虽然有利于降低挠度,但提高了加工控制难度,部件的强度和形位精度都难以得到保障。
1.2 设计依据和结果
文献[8]中,未经准直的阴极末端挠度约为6.8 cm。为保证准直原理验证的可参考性,将Mini-MITL的末端挠度w设计为6 cm左右。受实验室安装场地的空间限制,阴极总长l不宜超过8 m。根据装置MITL阴极实际可能分为4~6节,将Mini-MITL均分为5节。此外,兼顾挠度大小和加工形变控制难度,阴极筒壁厚约为10 mm。根据上述基础设计参数,综合考虑经济性、可加工性以及装配调整的可操作性,经过多次仿真估算,将圆筒的长度定为每节1.6 m,每节分为长度相等的阶梯式两段,后半段比前半段直径减小2 mm,用于模拟阴极直径根据阻抗匹配而变化的结构设计,因此外观上阴极共有10段;壁厚8 mm,外径最大处为176 mm,最小处156 mm,上一级后半段与下一级前半段的外径相同,如图1(a)所示。所选用的阴极材料为6061-T6铝合金,在SolidWorks Simulation系统环境设置中,其弹性模量E=69 GPa,密度ρ=2700 kg/m3。在该尺寸参数设计下,末端的挠度变形仿真值(附加垫片)为59.10 mm,如图1(b)所示,结果符合预期。

(a) Mini-MITL 阴极示意图(a) Illustration of Mini-MITL cathode stalk

(b) 所设计阴极的变形仿真结果(b) Deflection simulation result of the designed stalk图1 Mini-MITL阴极示意图及变形仿真结果Fig.1 Illustration and deflection simulation result of Mini-MITL cathode stalk
为便于操作定位,垫片螺孔数量应取4的倍数为宜。兼顾考虑螺孔间距大小和步进调节精度,并同时参考文献[8]中12~24个螺孔数量,设计中每个倾斜垫片采用16个均匀分布的螺孔,则步进旋转角度为22.5°。根据GB/T4096-2001,选择棱体斜度最小的1 ∶500作为切斜垫片的加工斜度,即(xxi,yyi)。需要指出的是,所选择的斜度必须经过验算,防止斜度过小,不能将阴极筒挠度完全抵消。未进行斜面加工的垫片厚度为10 mm,由于斜度很小,在进行数值建模时,可近似认为垫片为等厚度圆柱体。每组垫片的倾斜端面相切,垂直端面分别与上一节圆筒末端和下一节圆筒始端相切,如图2(a)所示。
定义倾斜垫片最厚处的螺孔为标志孔,标志孔中心与垫片中心之间的连线为标志线,标志线与竖直线之间的角度为垫片旋转角度,正面向左旋转(顺时针)为正,反之为负。定义每组垫片中的靠近低压端的垫片称为“内侧垫片”,另一片则称为“外侧垫片”。假设各组倾斜垫片旋转角度分别为(xxi,yyi)(内侧垫片)、(xxi,yyi)(外侧垫片),(xxi,yyi)为各节的编号,如图2(b)所示。
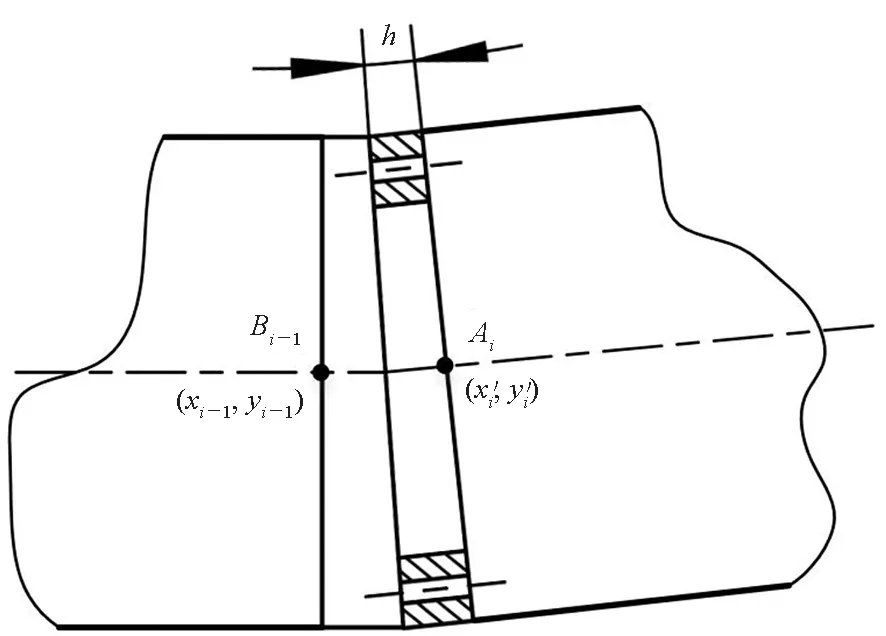
(a) 倾斜垫片连接局部示意图(a) Local illustration of tilt spacer connection

(b)各组倾斜垫片转角示意图(b) Illustration of rotating angle of each set of tilt spacers图2 各节阴极筒端面中心的数值建模Fig.2 Center coordinate numerical modelling of the ends of each stalk segment
2 坐标数值建模
2.1 建模过程
假设圆筒长度都为l,垫片厚度都为h(倾角造成的偏差很小,建模时将其忽略),第一节始端的法兰厚度为δ。每节始端中心点分别记为Ai,每节末端中心点分别记为Bi,如图2(a)所示,阴极根部(首节垫片左端面)中心点记为B0,各点的仿真挠度分别为di。在每组倾斜垫片的调节作用下,水平方向与竖直方向相对偏角分别为:
(3)
其中,λ为单个倾斜垫片的倾斜角。将B0点作为参考点,并称之为“理想原点”,不考虑阴极的轴向坐标,只考虑截面的径向坐标。根据上述约定,B0坐标为(0,0),假设Bi偏离理想原点的坐标为(xi,yi),Ai偏离理想原点的坐标为(x′i,y′i),则对于第一节存在如下的理论数值关系:
(4)
(5)
以后各节的坐标应为该节之前所有倾斜垫片导致的相对偏角之累积结果,这里需要注意每组倾斜垫片中内侧垫片的偏角会累加到外侧垫片,即存在如下关系式:
(6)
(7)
其中,i=2,3,4,5。
上述数值建模过程同时适用于倾斜垫片旋转角度为离散调节和连续调节两种情况,如果目标坐标(xi,yi)或(x′i,y′i)已知,则可将公式进行逆向求解得到θi、ηi的值。
2.2 模型验证
以上数值建模得到每节阴极筒始端和末端的相对坐标,对于每节中间点的坐标可进行线性插值计算。将每节中间点和末端点作为准直建模的参考点,本文称这些点为“关键节点”,并设其坐标为(xxi,yyi) (i=1,2,…,10)。为验证上述数值建模方法的正确性,试用一套倾斜垫片转角组合,各组垫片的转角如表1中第2、3列所示。在此转角组合下进行实体建模,得到的yyi坐标值如表1中第5列所示;采用上述数值建模方法得到的yyi坐标值如表1中第6列所示;二者误差如表1中第7列所示。可以看出,数值建模方法得到的坐标值误差很小,处于微米量级,因此认为数值建模方法正确有效。经分析,误差产生的主要原因是倾斜垫片的中心厚度应略小于h,但建模时是按照h进行计算的。上述建模方法在理论上给出了倾斜垫片在不同调整角度下的修正量计算方法。
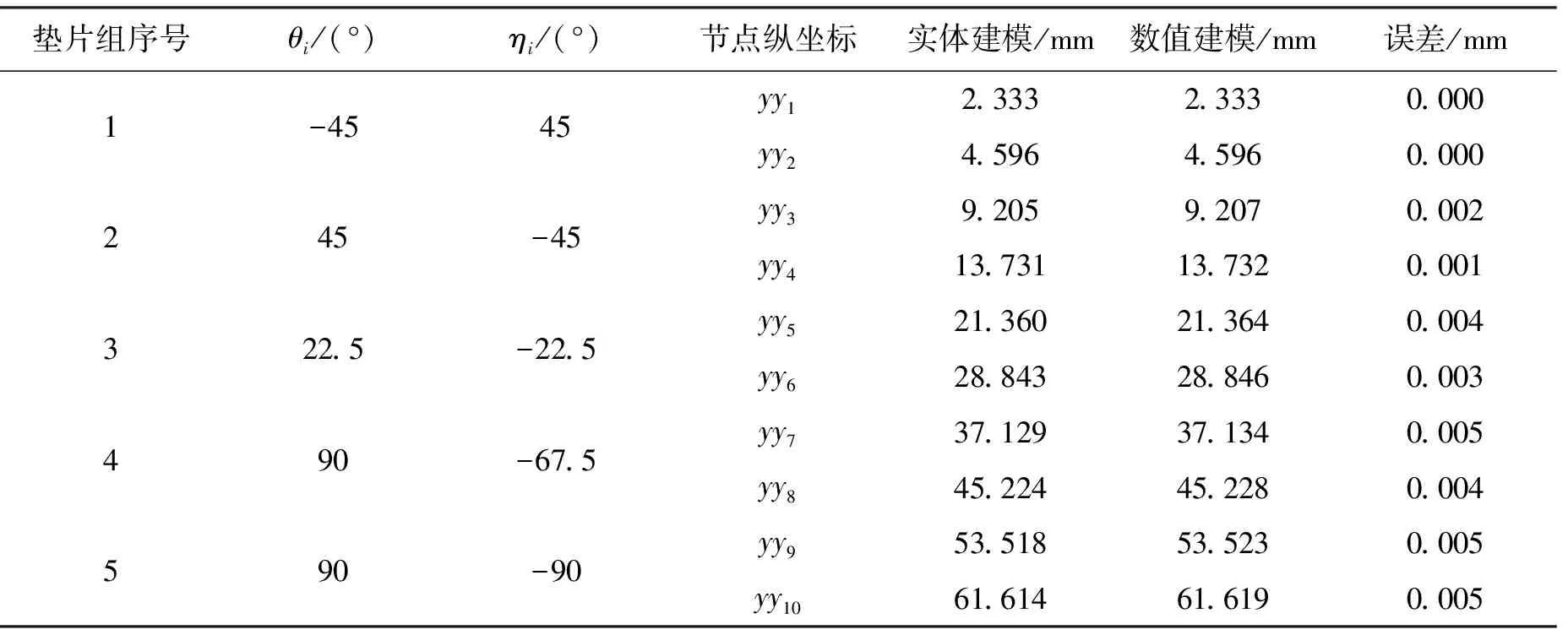
表1 仿真与数值建模坐标比较
3 准直策略与结果分析
3.1 准直调节策略
在前两节内容中,分别研究了Mini-MITL的设计过程和倾斜垫片作用下的关键节点坐标数值建模方法。由于重力作用,阴极筒在各个关键节点处都会产生不同程度的挠度变形,造成节点坐标的偏移,阴极筒的真实形位应是倾斜垫片修正量和挠度变形两个因素的叠加。由于重力引起的挠度变形只体现在竖直方向,水平方向不受影响。换言之,关键节点的水平坐标只取决于倾斜垫片的水平修正量,而竖直坐标则为挠度变形量与垫片修正量之差。
理论上,由于重力大小不变,后一节倾斜垫片的相对旋转角度并不会对前一节坐标产生影响,所以可以采用从低压端到高压端进行顺序调节的方法,依次选取各组倾斜垫片的旋转角度,使得每个关键节点的水平和竖直方向直线度误差都处于阈值范围内。在进行转角赋值的过程中,由于垫片的调整是有限的步进角度,因此可以采取试凑的方法进行。具体实现途径是首先根据挠度仿真结果和数值模型,用理论计算的方法得到各组倾斜垫片的最优转角,在此基础上进行二次赋值,选择与最优转角接近的离散步进角度。最后将初选的离散步进角度代入数值模型计算准直效果,从而选择确定准直效果最好的离散步进角度。
3.2 Mini-MITL准直理论结果
理论和实验研究表明,阴阳极间隙的整体误差阈值为阴阳极间隙的5%。经过误差分配,Hermes装置的阴极筒准直调节的误差阈值为1.3 mm[8]。国内的典型装置为中国工程物理研究院的50级LTD模块,该装置阴极筒准直的最大误差为1.48 mm[13]。在无法给出阴阳极间隙的前提下,参考上述两个装置,并综合考虑阴极长度因素,针对本研究中的Mini-MITL设计,将准直阈值设定为整数1 mm。在SolidWorks仿真环境中,仿真得到各个关键节点的挠度变形如表2中第4列所示。根据上一小节提出的准直策略,调整各组倾斜垫片的相对旋转角度,依次使下一节的关键节点坐标处于所规定的阈值范围内。经过试凑,各组倾斜垫片的旋转角度如表2中第2、3列所示,准直后的各个关键节点的竖直方向修正量如第5列所示。在倾斜垫片的修正下,水平方向和竖直方向的关键节点坐标相对于理想状态的偏差如图3所示,可以看出水平和竖直方向的直线度指标均在阈值范围内,符合规定的阈值要求。需要指出的是,从图3中可以看出,第一节圆筒中间点(即第一个关键节点)的竖直方向误差比较大,并且该误差比后续几节中间点处误差更难补偿,这是因为首节的挠度变形曲率最大,但基于倾斜垫片的调节策略是线性的。
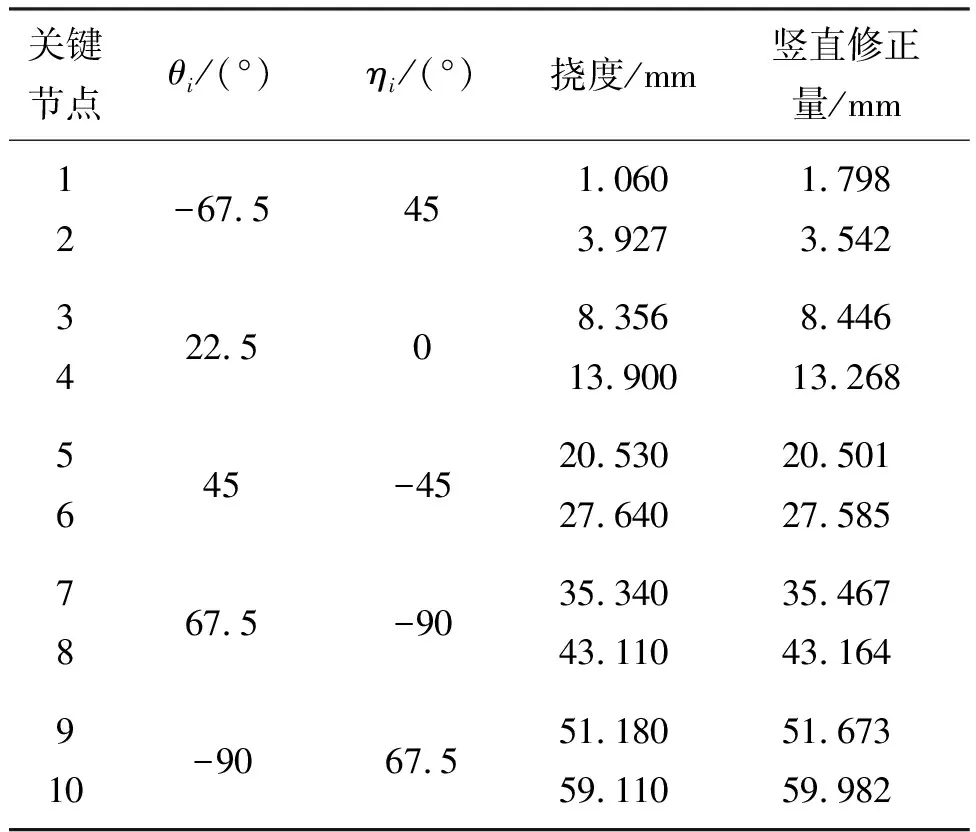
表2 Mini-MITL准直结果
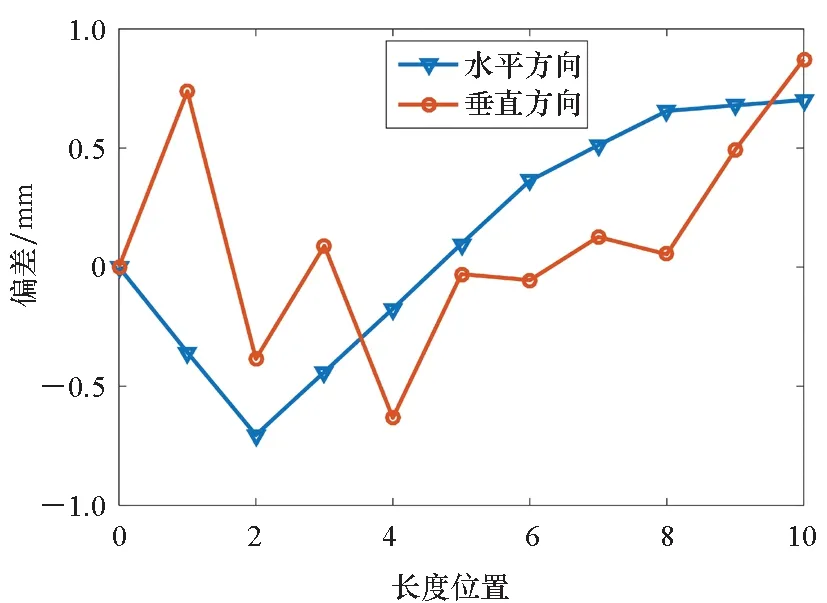
图3 离散调节策略下的理论准直结果Fig.3 Theoretical alignment result with discretely adjusting strategy
3.3 准直策略改进优化
3.1节所述的准直策略是基于倾斜垫片角度离散步进的前提进行的。这种策略的优点是在阴极的整体装配过程中,由于倾斜垫片通过穿孔定位,容易实现旋转角度的定位和调节。但相应的缺点也较明显,一是离散步进角度的确定需要经过理论计算后的二次赋值,效率较低;二是理论计算的最优转角与最终确定的离散转角可能有较大偏差,不能充分发挥倾斜垫片的调节作用。
针对上述问题,进一步研究采用倾斜垫片的连续可调方式。具体设计中,相邻两节阴极筒的螺栓连接不穿过倾斜垫片,而是通过螺栓的预紧力将倾斜垫片压紧锁定。改进后,倾斜垫片的旋转角度可以不受孔位的限制,实现连续可调,实际旋转角度能够与理论计算角度保持一致,将倾斜垫片的调节效果最大化。利用2.1节中所建立的数值模型,将各节末端目标坐标分别设置为(0, -0.4),(0, -0.2),(0, 0),(0, 0),(0, 0),反向求解各组倾斜垫片的旋转角度。将第一、第二节末端垂直坐标分别设置为-0.4和-0.2的目的是控制每节阴极筒的中点坐标,若都设置为0则会导致中点坐标偏大。在改进后的准直策略下,水平方向和竖直方向的关键节点坐标相对于理想状态的偏差如图4所示。可以看出,采用连续可调方式后,调节后坐标与目标坐标相吻合,水平方向和竖直方向的理论准直误差均优于离散调节,水平方向在理论上可以实现零误差,竖直方向的误差也呈逐级降低趋势,达到了预期的效果。但应指出的是,该方法在装配过程中旋转角度难以定位,需要在倾斜垫片的圆周方向进行较为密集的角度标记。

图4 连续调节策略下的理论准直结果Fig.4 Theoretical alignment result with continuously strategy
3.4 工程实际中的影响因素分析
大型磁绝缘传输线的阴极杆准直是装置建设中的最具挑战性的工程性难题,工件的加工误差和装配过程中的应力控制等因素都会对最终的准直效果产生重要影响。根据目前的文献调研情况,尚未发现有针对性的研究内容报道。由于前述Mini-MITL未付诸加工,尚不具备实验验证条件,本小节先对工程实际中影响准直的工件加工误差和装配应力控制进行初步分析,以用于指导工程实施。
1)工件加工误差。倾斜垫片的平面度、斜度,阴极筒的圆柱度、端面平面度、平行度等诸多形位公差精度指标都会对最终的装配结果产生影响,并且越靠近阴极根部的工件加工误差对准直的影响越大。因此,首先应对工件(尤其是靠近根部的工件)加工形位公差提出严格要求,达到IT7甚至IT6以上的加工精度。在此基础上,对加工误差影响的处理手段有正反两种,第一种是正向处理,即首先对工件加工精度进行测量,将测量结果统筹纳入数值模型中,对倾斜垫片的调整角度进行预先修正;第二种是反向处理,即暂不考虑加工误差,仍先按预定方案进行调节,根据准直测量结果与理论精度进行对比,从而对倾斜垫片调整角度进行修正。两种手段各有优劣,工程实际中应经过试验后进行综合评判选用。
2)装配应力控制。根据螺栓连接的理论分析,螺栓预紧力越大,工件对应连接位置的压缩形变越大。对于倾斜垫片的圆周螺栓阵列,某个方向的预紧力越大,阴极向该方向的翘曲越明显,这个结果已经过工程实践验证。因此,为了充分强化理论建模对准直过程的指导作用,应对螺栓连接的预紧力进行精确控制,具体实施方法是采用力矩扳手,事先设定预紧力矩大小。此外,在预紧的过程中应对称循序进行,以尽量保证连接后的工件在圆周方向受力均匀一致。
4 结论
基于倾斜垫片的MITL阴极准直方法的难点之一在于如何确定垫片的相对旋转角度,使得调节后的直线度指标处于所规定的阈值范围内。关键节点坐标的数值建模方法的有效性得到了三维实体仿真结果的验证,模型误差可以控制在微米量级,能够满足准直调节的工程实施需求。以此为基础,采用逐级确定的准直策略,可以将整个Mini-MITL阴极筒的直线度误差控制在阈值内,基本满足了设计要求。改进后的连续调节方式比离散调节的准直精度更高,有必要在工程实际中尝试应用。
需要指出的是,上述研究内容只从理论上给出了基于倾斜垫片的阴极直线度调节方法。工程实际中,除了3.4节中分析的工件加工误差和装配应力控制,还有材料属性、紧固件重力、悬臂支架自身变形等因素的存在,准直调节的过程要比理论分析更加复杂。在进一步的工作中,应继续研究如何将这些因素统筹纳入理论模型中进行综合考虑,通过工程实践总结出更具指导性的准直方案。

