拦截高速机动目标的捕获区及微分对策导引律*

毛柏源，李君龙，张 锐，张鹏飞

(北京电子工程总体研究所， 北京 100854)

近年来，高速机动目标拦截技术逐渐成为现代防御系统的研究热点，传统的比例导引律已在低速非机动目标的攻击场景中获得了广泛的应用，并且效果良好。但对于高速机动目标的拦截，比例导引并不适用，因此对机动目标拦截的导引律研究具有重要意义。

文献[1-2]基于非奇异终端滑模控制理论设计了碰撞角约束下的滑模导引律，能够使系统状态在有限时间收敛。文献[3]基于零化视线转率，针对机动目标拦截问题，提出一种非线性微分几何导引律，采用非线性控制理论削弱了目标机动带来的影响。文献[4]采用最优控制方法实现了在时间和角度同时约束条件下对机动目标和非机动目标的拦截。

相对于其他导引律，微分对策导引律的优势在于其只需要目标的机动能力，而不需要其未来的具体机动形式。文献[5]将机动目标拦截问题转化为零和微分对策问题，并得到了状态依赖里卡蒂微分方程的解，从而推导了微分对策导引律，该导引律不需要对剩余时间进行精确估计。文献[6]将微分对策导引律应用于多导弹协同拦截问题，多个导弹共同组成对策一方，得到的导引律使得导弹组从不同角度对目标实施拦截。文献[7]通过引入适当的性能函数，将鲁棒控制转化为两人零和微分对策问题，仿真验证了所提出鲁棒导引律的有效性。文献[8]针对固定末端时刻拦截机动目标的制导系统，构建了非线性有限时间微分对策框架，利用一个具有时变权值和激活函数的评价网络来逼近哈密顿-雅可比方程(Hamilton-Jacobi-Isaacs, HJI)方程的解，得到了基于自适应最优控制的有限时间微分对策制导律。从目前文献来看，微分对策导引律已被广泛应用于协同制导以及机动目标拦截等领域，但将其应用于捕获区的研究较少。

捕获区作为制导性能的一种评价依据，对它的深入研究意义重大，文献[9]推导了顺轨和逆轨的零控拦截条件，并得到了比例和反比例的捕获区。文献[10]通过引入弹目相对运动的单位角动量，将传统的捕获区描述转化为捕获长度描述，推导了三维空间内的理想比例导引律的捕获区。但上述捕获区的推导均是基于比例导引律，在机动目标拦截场景中的应用受到限制。

针对机动目标拦截时，弹目均具有任意阶动力学特性的情形，本文基于微分对策理论推导了一种线性化拦截场景中的解析形式捕获区，并具体到直/气复合控制导弹对机动目标的拦截中，之后重新选取性能指标，将目标与直/气复合控制导弹在末端带有碰撞角约束的制导问题转化为零和微分对策问题，通过求解弹目最优拦截策略，将鞍点解的存在条件转化为制导增益的约束问题。仿真验证了几种情形下直/气复合控制导弹对目标实施拦截的捕获区存在域，同时，导引律仿真结果表明微分对策制导方法在目标机动形式未知的情形下能够实现多种碰撞角约束的预期拦截。

1 弹目运动描述

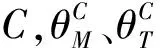
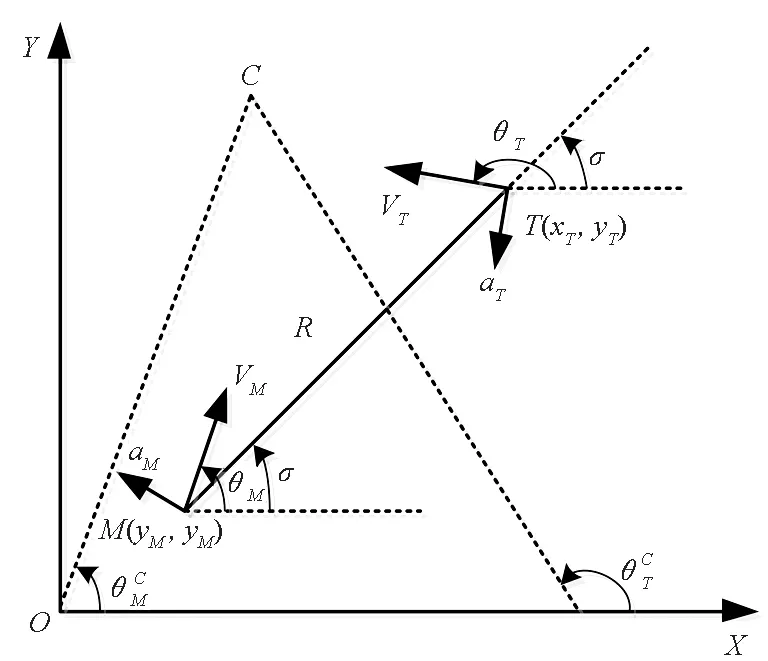
图1 弹目拦截几何示意图Fig.1 Schematic of missile-target planar interception geometry

x=xT-xM

(1)

y=yT-yM

(2)

(3)

(4)

(5)

(6)

由导弹、目标在XOY平面内的相对位置可知，弹目交汇可看作沿x轴方向逐渐接近的运动，y轴方向上的位移差可看作是脱靶量。定义末制导剩余时间为tgo=tf-t，初始时刻为t0，当导弹击中目标时，设t=tf，此时弹目相对法向速度为零，则

VTsin(θT-σ)=VMsin(θM-σ)

(7)

为不失一般性，本文的研究基于以下假设。

假设1在末制导阶段，认为导弹和目标速度大小不变，并且弹目机动相对于两者的速度为小量。

假设2认为导弹和目标的控制输入均有界。

假设3末制导过程中，导弹和目标偏离初始碰撞三角形较小。

根据假设3，引入一个小量

(8)

式中，j∈{T,M}，本文中下标j含义相同。

则得到

(9)

结合式(4)、式(7)、式(9)可得

(10)

结合式(5)、式(6)、式(10)可得

(11)

通常，在带有碰撞角度约束的拦截场景中，碰撞角度定义为导弹击中目标时其速度矢量与目标速度矢量的夹角，即

(12)

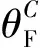
考虑一类系统的任意阶控制动力学方程，则

(13)

(14)

(15)

(16)

为后续推导方便，选取如下状态变量

(17)

根据式(5)、式(6)、式(11)、式(12)及式(13)可得到导弹与目标相对运动方程如下

(18)

式中

2 捕获区存在条件分析

2.1 复合控制导弹末制导段捕获区分析

为研究方便，采用文献[11]中的终端投影方法，对式(18)进行降阶处理。

(19)

式中，Z(t)为降阶处理后重新定义的状态向量，该向量的物理意义是导弹与目标从当前时刻开始不加任何控制，直至弹目遭遇所产生的脱靶量和碰撞角。其中，z1(t)代表零控脱靶量(Zero Effort Miss distance，ZEM)，z2(t)代表零控碰撞角(Zero Effort impact Angle，ZEA)。Φ(tf,t)为系统式(18)的状态转移矩阵，D为常数矩阵，其取值如下

(20)

对式(19)求导可得

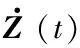
=DΦ(tf,t)(BMuM+BTuT)

(21)

系统降阶后，首先研究z1(t)与弹目双方机动策略之间的关系。由式(21)可设

(22)

式中，fM(tf,t)≜D1Φ1(tf,t)BM1，fT(tf,t)≜D1Φ1(tf,t)BT1，其中D1、Φ1(tf,t)、BM1、BT1为式(17)选择前四个状态变量时对应的矩阵。

基于z1(t)选取如下性能指标函数

Jz1=|z1(tf)|

(23)

根据式(22)构造哈密顿函数

=λz1[fM(tf,t)uM+fT(tf,t)uT]

(24)

式中，λz1为待定的拉格朗日乘子。

则弹目最优拦截策略为

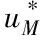
(25)

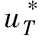
(26)

协态方程及横截条件为

(27)

可得

λz1=sign[z1(tf)]

(28)

结合以上条件，将式(22)从t到tf积分，得到z1(t)的最优轨迹为

(29)

其中

(30)

针对目标机动未知的情形，为了研究对策双方在拦截末段的捕获区存在条件，首先给出捕获区定义及相关引理如下。

定义1具有非零初始条件的拦截弹能够对目标实现精确拦截的空间区域称为捕获区。

(31)

引理1[12]在线性一对一拦截情形中，捕获区存在的充分必要条件是

∀t∈[t0,tf]

(32)

定理1当系统式(13)描述对策双方的自动驾驶仪动态特性，且最优拦截轨迹满足式(29)时，在一对一拦截情形中必然存在如下形式的捕获区。

证明:针对系统式(13)，可得出其传递函数为

(34)

本文为了方便研究，将其中任一传递函数简化为

(35)

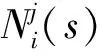
(36)

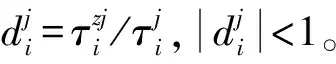
对式(22)中的D1Φ1(tf,t)Bj1进行拉普拉斯反变换可得

D1Φ1(tf,t)Bj1=D1Φ1(tf-t)Bj1

(37)

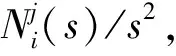
则由fj(tf,t)≜D1Φ1(tf,t)Bj1可得

(39)

(40)

由式(39)、式(40)可知

(41)

根据引理1可知，式(41)满足捕获区存在条件。因此，若选择了系统式(13)描述的对策双方自动驾驶仪动态特性，则在一对一拦截情形中必然存在捕获区，下面将推导捕获区的解析表达式。

本文基于直/气复合控制拦截弹，主要研究在线性一对一拦截情形中的捕获区存在条件。结合定理1，分别选择导弹与目标的自动驾驶仪动态特性传递函数如下

(42)

(43)

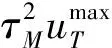
(44)

(45)

则由式(22)可得

(46)

将式(25)、式(26)代入式(46)，并对t从0到tgo积分，得到

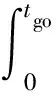
(47)

式中

(48)

□

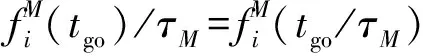
2.2 基于碰撞角约束的微分对策问题研究

2.1节定性分析了复合控制导弹对于机动目标在拦截末段的捕获区问题，本节针对式(18)所示的系统，主要研究基于直/气复合控制的拦截弹与机动目标在末制导段带终端碰撞角约束的微分对策问题。

设性能指标如下

(50)

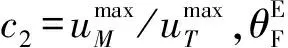
(52)

(53)

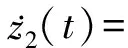
uM[τε1Mg2(τM)+τε2M]/VM

(54)

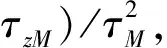
(55)

由协态方程及横截条件可得

(56)

基于以上条件可得弹、目最优拦截策略为

(58)

将式(57)、式(58)代入式(53)、式(54)，并从t到tf积分，可得末端时刻状态

(59)

(60)

式中

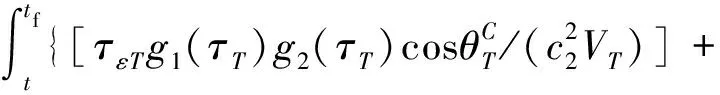
[(τε1Mg1(τM)+τε2Mtgo)×

(62)

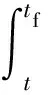
[(τε1Mg2(τM)+τε2M)/VM]2}dφ

(63)

(64)

再将式(59)、式(60)代入式(57)、式(58)可得导弹、目标最优拦截策略表示为零控脱靶量与零控碰撞角误差的线性组合形式

(65)

(66)

式中，tgo代表剩余飞行时间，其由弹目距离除以弹目相对速度沿视线的分量得到，KM1、KM2、KT2、KT2代表制导增益。

(68)

(69)

(70)

对于弹目双方零和微分对策问题，鞍点解存在当且仅当系统式(18)对应的下列里卡蒂微分方程的解有限。

(71)

式中，P(tf)=diag(c0,0,0,0,c1)，而P(t)有限的充分条件是制导增益有界，故当式(67)～(70)有界的情况下才存在鞍点解。通过对性能指标式(50)分析可知，只有当c0,c1→∞时才满足理想拦截情形，故参数c0,c1的选取需要综合制导增益与性能指标进行确定。

由于微分对策中鞍点解的存在要求制导增益KM1、KM2、KT1、KT2有界，故应从制导增益与c0,c1的关系来着手分析选取原则。首先，考虑满足脱靶量指标c0→∞，而c1取为有限值时的制导增益变化趋势；然后，进一步分析目标无机动c2→∞，此时制导增益随c1取值的变化趋势，由此可以得到使制导增益有界，即分母不为零的约束方程，从而反向推导c0,c1的取值范围。

3 仿真分析

本节首先基于式(49)给出的弹目沿最优拦截轨迹运动时的捕获区解析式进行了仿真验证，之后，将目标与直/气复合控制导弹在末端带有碰撞角约束的制导问题转化为零和微分对策问题，并对导引律进行仿真分析。

情形1：拦截弹采用直/气复合控制与纯气动力控制捕获区对比分析，仿真结果如图2所示。

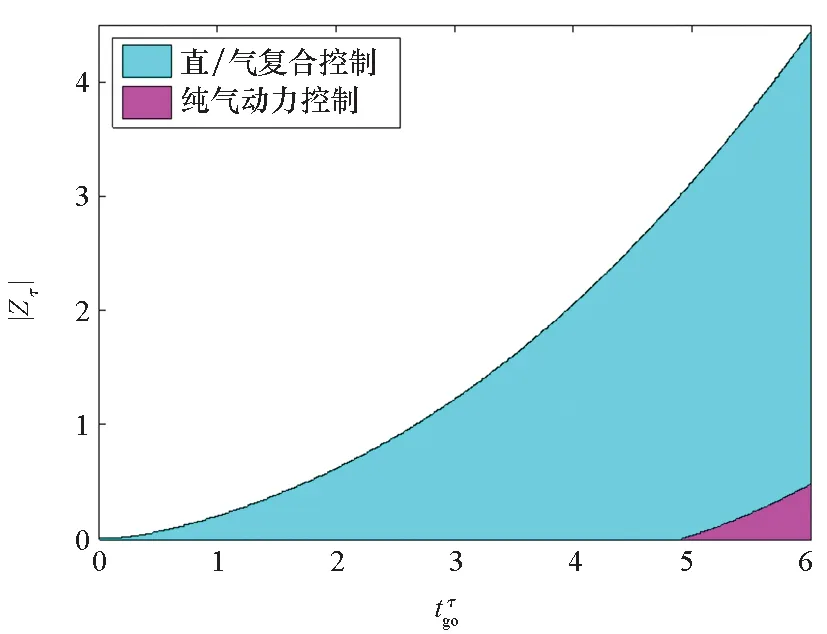
图2 捕获区分析：情形1Fig.2 Analysis of capture zones: scenario 1

图2为拦截弹采用直/气复合控制与纯气动控制情形下在Zτ=0轴上方的捕获区范围，全域内捕获区关于Zτ=0轴上下对称。仿真结果表明，采用复合控制时的捕获区范围远大于采用纯气动力控制的，这也说明直/气复合控制导弹在拦截末段具有更大的优势。

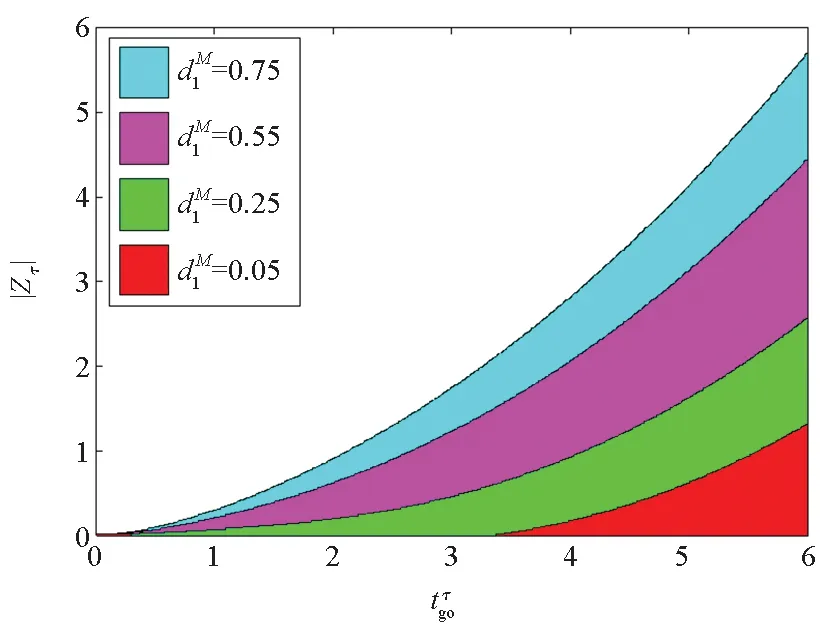
图3 捕获区分析：情形2Fig.3 Analysis of capture zones: scenario 2

情形3：拦截弹的直接力作用装置安装于质心前后时的捕获区对比分析，仿真结果如图4所示。

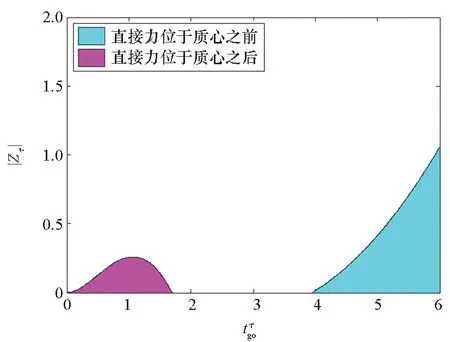
图4 捕获区分析：情形3Fig.4 Analysis of capture zones: scenario 3

情形4：拦截弹与目标的最大机动能力比值μ1对捕获区的影响分析，仿真结果如图5所示。

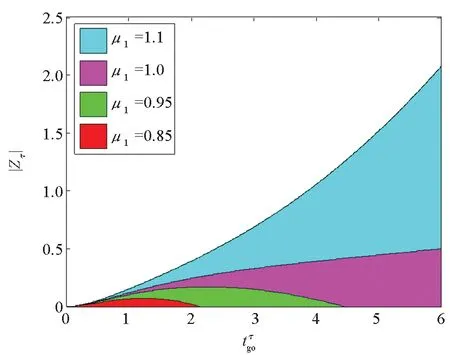
图5 捕获区分析：情形4Fig.5 Analysis of capture zones: scenario 4

图5表明，当μ1<1之后，导弹对目标的捕获区迅速减小，表明拦截弹需要更大的机动能力以确保对目标具有足够大的捕获区。

针对本文提出的微分对策导引律，首先在不同碰撞角约束下进行仿真验证。为了进一步验证本文提出的微分对策导引律的性能，与文献[16]中的最优导引律(Optimal Guidance Law，OGL)、文献[17]中的自适应滑模导引律(Adaptive Sliding Mode Guidance Law, ASMGL)进行对比仿真，本文的记为微分对策导引律(Differential Game Guidance Law， DGGL)。从末制导时刻开始，机动目标的初始位置为(30 km，15 km)，目标速度为VT=1 500 m/s。拦截导弹的初始位置为(0 km，12 km)，速度为VM=900 m/s。仿真参数取值为c0=105，c1=108，c2=5，θM=10°，θT=180°。

五种碰撞角约束下的微分对策导引律仿真结果如图6～10所示。

由图6～10可知，本文提出的微分对策导引律在不同的碰撞角约束下均能实现预期拦截，并且零控脱靶量及零控碰撞角误差均能收敛到零附近，同时导弹的指令加速度不超过6g，这表明该导引律鲁棒性良好，脱靶量小，易于工程实现。

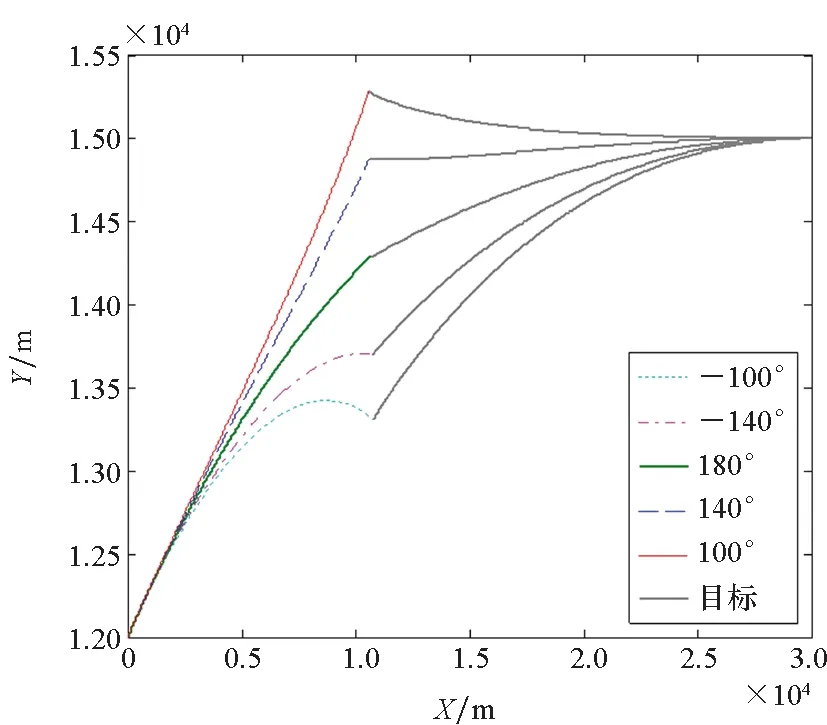
图6 不同碰撞角弹道Fig.6 Trajectories of different collision angles

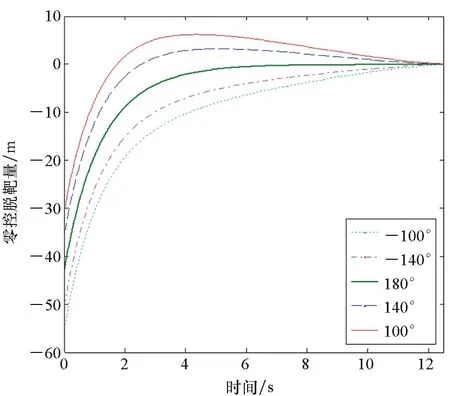
图7 不同碰撞角对应的零控脱靶量Fig.7 ZEM of different collision angles

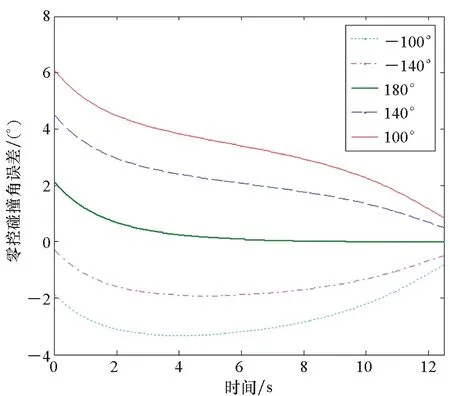
图8 不同碰撞角对应的零控碰撞角误差Fig.8 ZEA error of different collision angles

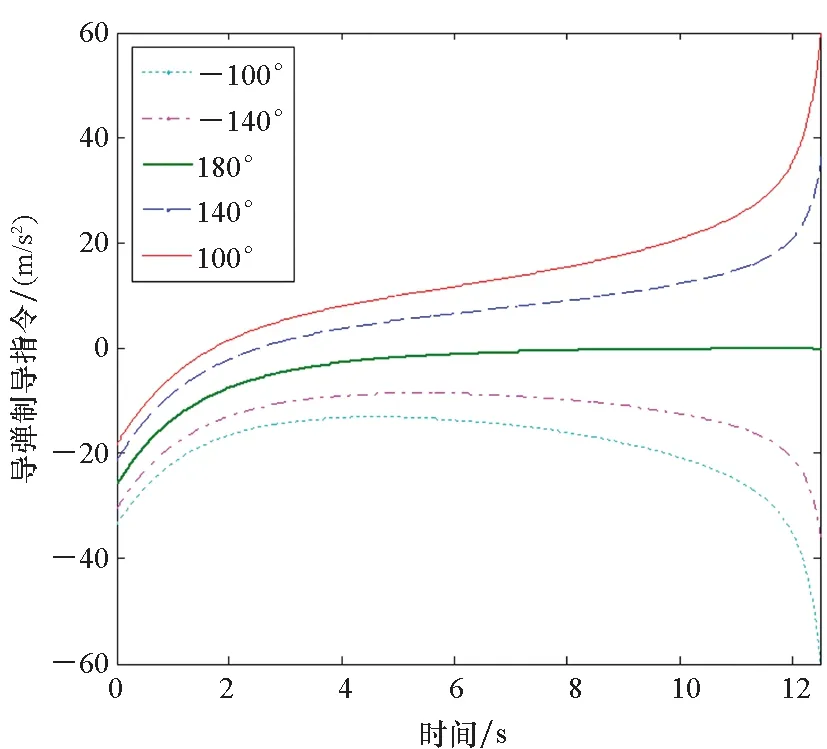
图9 不同碰撞角对应的导弹制导指令Fig.9 Missile′s guidance command of different collision angles

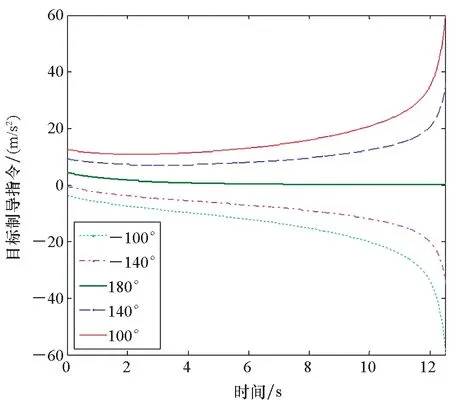
图10 不同碰撞角对应的目标制导指令Fig.10 Target′s guidance command of different collision angles

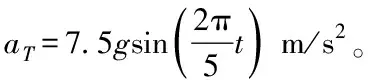
图11 拦截弹道对比Fig.11 Comparison of interception trajectories

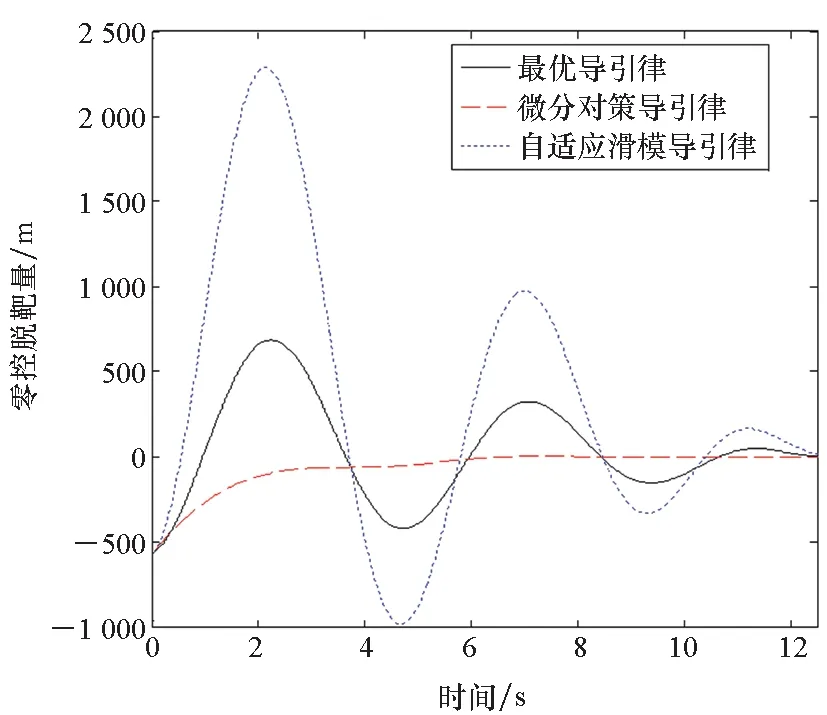
图12 零控脱靶量对比Fig.12 Comparison of ZEM

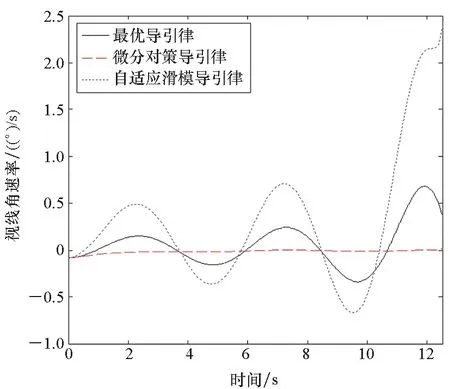
图13 视线角速率对比Fig.13 Comparison of line of sight angular rate

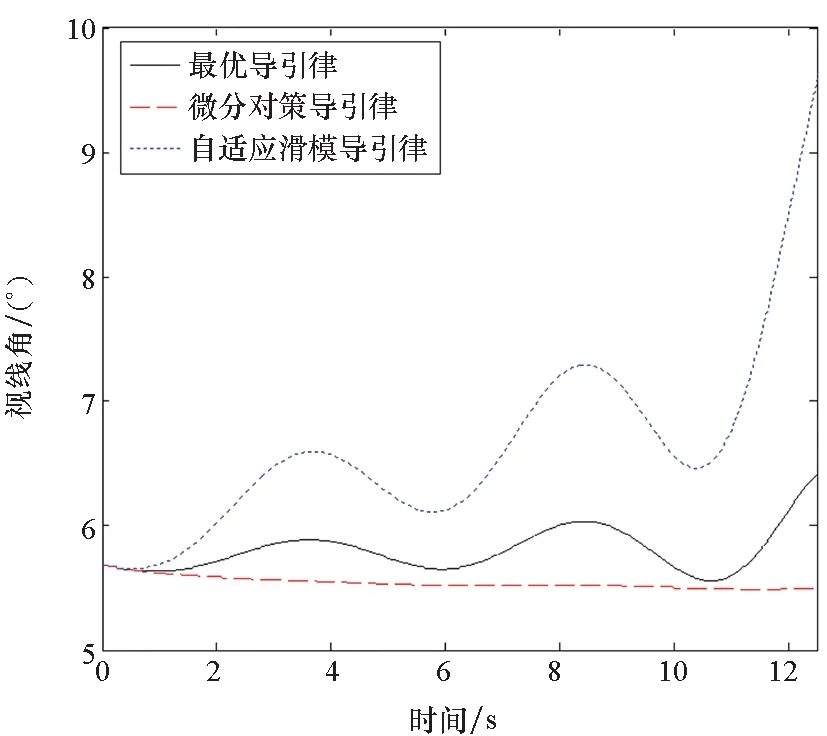
图14 视线角对比Fig.14 Comparison of line of sight angle

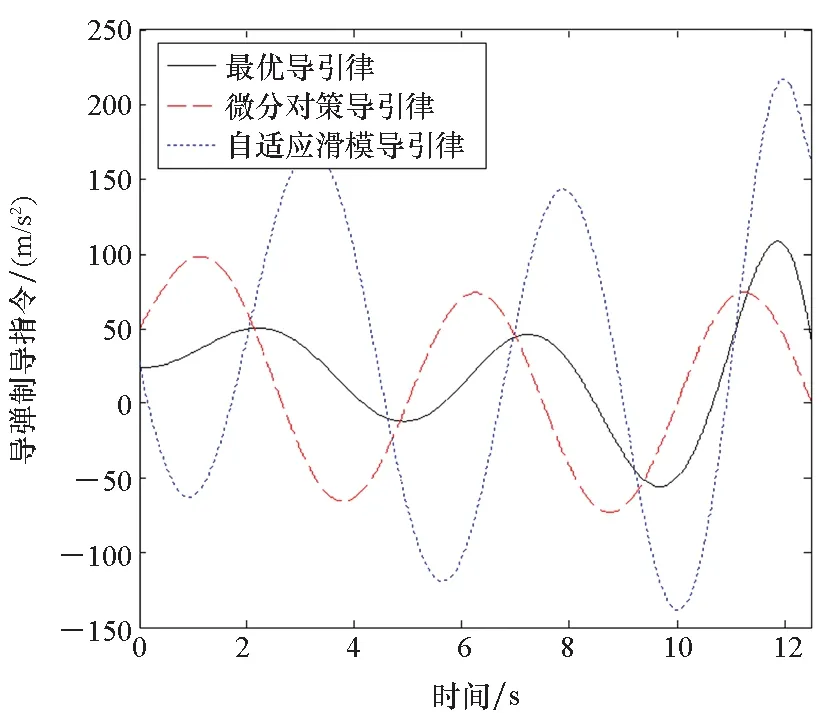
图15 导弹制导指令对比Fig.15 Comparison of missile′s guidance command

仿真结果表明，在三种导引律的拦截弹道中，自适应滑模导引律的弹道波动幅度最大，并且其ZEM也随目标机动呈现较大的上下波动，这是因为滑模导引律的制导目的是使视线角速率趋于零。由于最优导引律是在对目标机动形式精确预估的前提下，直接将导弹导引至预测拦截点，因此加速度指令在三种导引律中相对最小。微分对策导引律的优势在于对目标机动不敏感，因此视线角速率及零控脱靶量曲线最为平缓，并且随时间变化缓慢。

为了更充分地对比三种导引律的性能，根据导弹初始弹道倾角不同，选取三种拦截情形进行对比分析。仿真初值如表1所示。

表1 三种拦截情形初值

三种拦截情形下的脱靶量统计如表2所示。

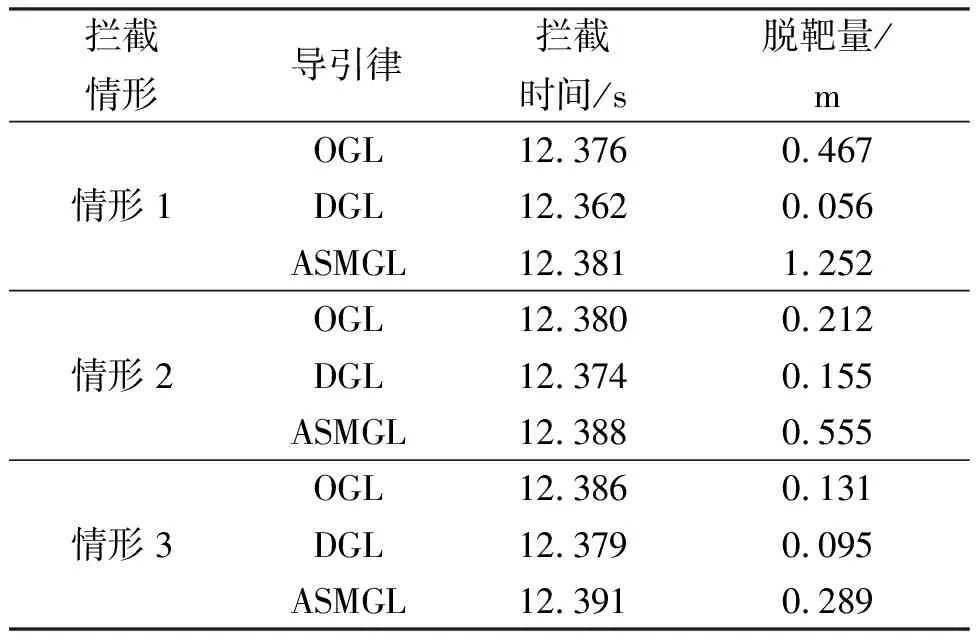
表2 仿真结果

通过对三种导引律进行多次仿真对比，表明针对正弦机动目标拦截，微分对策导引律的拦截末端脱靶量最小，制导精度最高。因为其对目标机动不敏感，视线角速度在末端能够收敛到零，这表明其在高速机动目标拦截场景中具有优良的制导性能。

4 结论

本文研究了高速机动目标拦截场景中的末制导段，通过简化弹目运动模型，基于微分对策理论推导出一种直/气复合控制导弹拦截目标的解析形式捕获区表达式。此外，为了得到带碰撞角度约束下的弹目最优拦截策略解析解，通过选取适当的性能指标，求解出两人零和微分对策问题，分别得到复合控制导弹与目标的最优拦截策略。仿真分析了几种情形下的捕获区范围，验证了捕获区的存在条件，导引律仿真结果表明，本文所提出的微分对策导引律在高速机动目标拦截场景中有优良的制导性能，其具有较高的工程实用价值。