重力扰动对SINS水平姿态的影响*

安 文，许江宁，吴 苗，李 峰

(1. 海军工程大学 电气工程学院， 湖北 武汉 430033； 2. 海军研究院， 北京 100161)

惯性导航系统(INS，Inertial Navigation System)是目前水下大型航行器最常用的导航方式，随着惯性测量单元(Inertial Measurement Unit, IMU)精度的提升，以及对导航精度要求的提高，重力扰动对INS的影响愈发凸显[1-3]，同时，重力扰动也成为限制惯性导航精度的重要因素[4]。尤其是水平重力扰动，1 mGal水平重力扰动约引起0.2″的水平姿态误差[5]，而水平重力扰动常常为几十到一百毫伽，个别地区可达到几百毫伽[6]。因此，有必要对重力扰动引起的INS导航误差的机理进行研究。

文献[7]将垂线偏差视为平台倾角误差，利用简化的垂线偏差统计模型推导了导航系统位置误差的均方差。文献[8]建立了包含重力扰动的捷联惯导系统(Strapdown INS, SINS)误差模型，仿真结果表明重力扰动垂直方向异常分量对惯性姿态测量系统的影响可以忽略，垂线偏差是影响系统精度的主要因素。文献[9]研究了扰动引力对弹道导弹命中精度的影响，为补偿地球扰动引力对导弹运动的影响提供了理论基础。文献[10]分析了重力扰动在定位定向系统中的误差传递，并提出一种实时的重力补偿方法。文献[11]研究了静基座下垂线偏差对INS初始对准的影响。文献[12]从重力扰动对惯性导航误差的影响机理分析入手，指出重力扰动是影响高精度零速修正导航精度的最主要误差源之一。文献[13]建立了包含重力扰动的惯导误差模型，分三种情况讨论了单通道下重力扰动矢量对INS的影响。文献[14]分别阐述了初始对准和纯惯导解算时，水平加速度计零偏与水平重力扰动间的耦合效应，重力扰动对惯导系统的影响等效为加速度计零偏。文献[15]设计了一个INS/GNSS组合导航仿真轨迹发生器，但仿真中并未加入重力扰动。

水平重力扰动与位置相关，根据重力场的球谐函数模型，可以认为水平重力扰动是一系列与位置有关的正弦函数的叠加。当载体发生位移时，水平重力扰动不能视为常量作用于INS，而应该视为一列不同幅值和频率的正弦波，因此有必要研究INS姿态误差与水平重力扰动间的幅频特性。但目前关于重力扰动与INS姿态误差之间关系的研究，主要存在两方面不足：一是没有给出运动条件下水平重力扰动与INS水平姿态误差间的误差传递表达式；二是没有研究组合导航模式下，重力扰动对INS水平姿态误差的影响。

本文以SINS为研究对象，首先推导了南北方向、东西方向匀速直线运动时，纯惯性解算的水平姿态误差与水平重力扰动间的传递函数；然后绘制了常用速度和位置范围内传递函数的零极点分布图；之后根据组合导航模式下的误差传递结构图，推导了组合导航模式下水平姿态误差与水平重力扰动间的传递函数；最后分别给出VN=10 m/s，L=30°和VE=10 m/s，L=30°时传递函数的Bode图，分析了纯惯性解算模式和组合导航模式下，传递函数的幅频特性，并针对如何提高SINS解算精度问题给出建议。

1 纯惯性解算时的误差传递函数

由于SINS高度通道发散，实际中常常引入阻尼，因此只研究水平回路。由于重力测量作业时，要求载体尽可能沿直线匀速航行，水平方向的匀速直线运动可以分解为南北方向的匀速直线运动和东西方向的匀速直线运动，因此分别分析两种方向匀速直线运动时水平重力扰动对SINS水平姿态误差的影响。定义当地地理坐标系(东-北-天)为导航坐标系(n系)，SINS误差方程为：

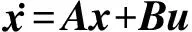
(1)

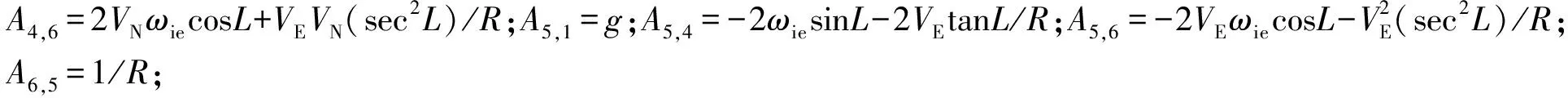
系统输出方程为：

Y=Hx

(2)

式中：Y=(φE,φN)T为输出量；H为2×7输出矩阵，H1,1=1，H2,2=1。

根据式(1)和式(2)，绘制系统输入、输出间的结构图，如图1所示。

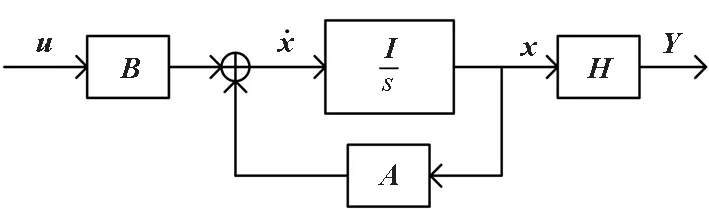
图1 式(1)和式(2)对应的系统结构图Fig.1 Diagram of system described by Eq.(1) & Eq.(2)

系统输入输出间的传递函数为：

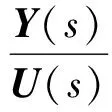
(3)

1.1 南北方向匀速直线运动

当载体沿南北方向匀速直线运动时，状态矩阵A中东向速度VE=0。根据式(1)～(3)和图1，得到南北方向匀速直线运动时SINS水平姿态误差与水平重力扰动间的传递函数为：

(4)

(5)

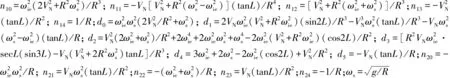
记式(4)和式(5)的极点为pi(i=1,2,3,…,6)，式(4)的零点为z1i(i=1,2,3,4)，式(5)的零点为z2i(i=1,2,3,4)，其中极点p1与p2，p3与p4，p5与p6，零点z11与z12，z13与z14，z21与z22，z23与z24分别互为共轭。

1.2 东西方向匀速直线运动

当载体沿东西方向匀速直线运动时，状态矩阵A中北向速度VN=0。根据式(1)～(3)和图1，得到东西方向匀速直线运动时SINS水平姿态误差与水平重力扰动间的传递函数为：

(6)

(7)

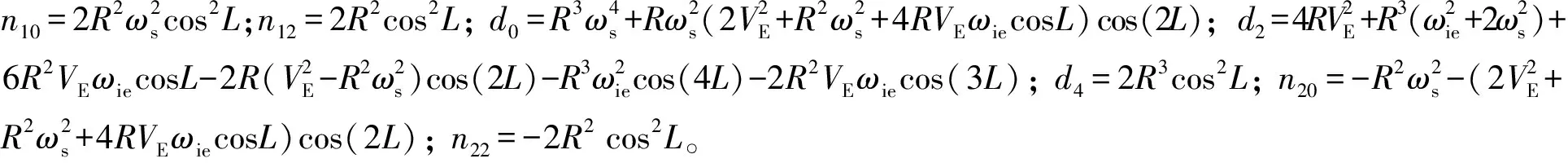
记式(6)和式(7)的极点为pi(i=1,2,3,4)，式(6)的零点为z11和z12，式(7)的零点为z21和z22，其中极点p1与p2，p3与p4，零点z11与z12，z21与z22分别互为共轭。

2 传递函数零极点分布

从式(4)～(7)可以看出，SINS水平姿态误差与水平重力扰动间的传递函数与载体速度和位置有关。图2显示了常用速度VN∈[-100 m/s,100 m/s]和位置L∈[0°,70°]范围内，传递函数式(4)和式(5)的零极点分布。从图2(a)可以看出，在上述速度和位置范围内，传递函数式(4)的零极点分布非常集中，有一对零极点p5、p6与z13、z14的分布虽然相对不集中，但这对零极点可以相消。从图2(b)可以看出，传递函数式(5)的零极点除了可对消的零极点对p5、p6与z23、z24之外，其他零极点的分布也非常集中。因此，可以选择上述速度和位置范围内任意一组速度和位置对应的传递函数的特征来代表整类运动模式下SINS水平姿态误差与水平重力扰动间的误差传递特征。

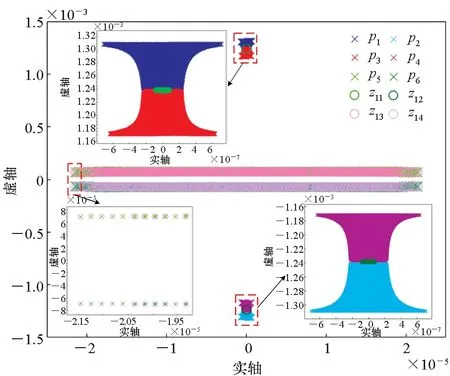
(a) 式(4)的零极点分布(a) Distribution of zeros and poles of Eq.(4)

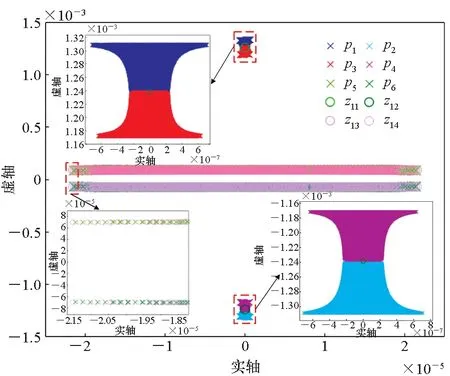
(b) 式(5)的零极点分布(b) Distribution of zeros and poles of Eq.(5)图2 南北方向运动的传递函数零极点分布Fig.2 Distribution of zeros and poles of transfer functions for north-south motion

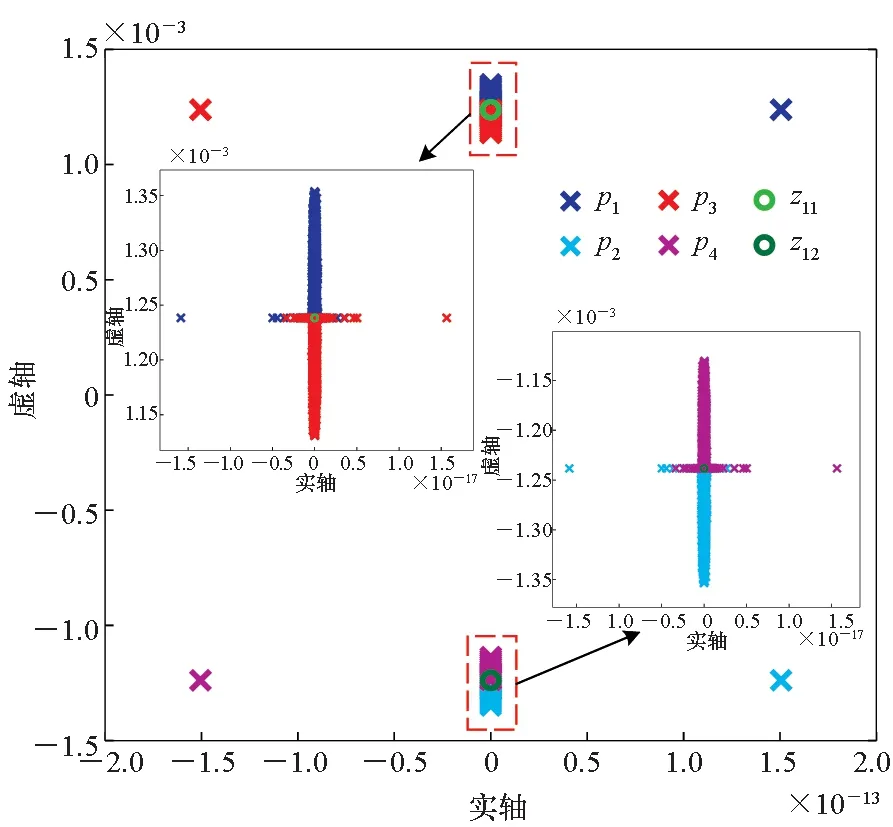
(a) 式(6)的零极点分布(a) Distribution of zeros and poles of Eq.(6)

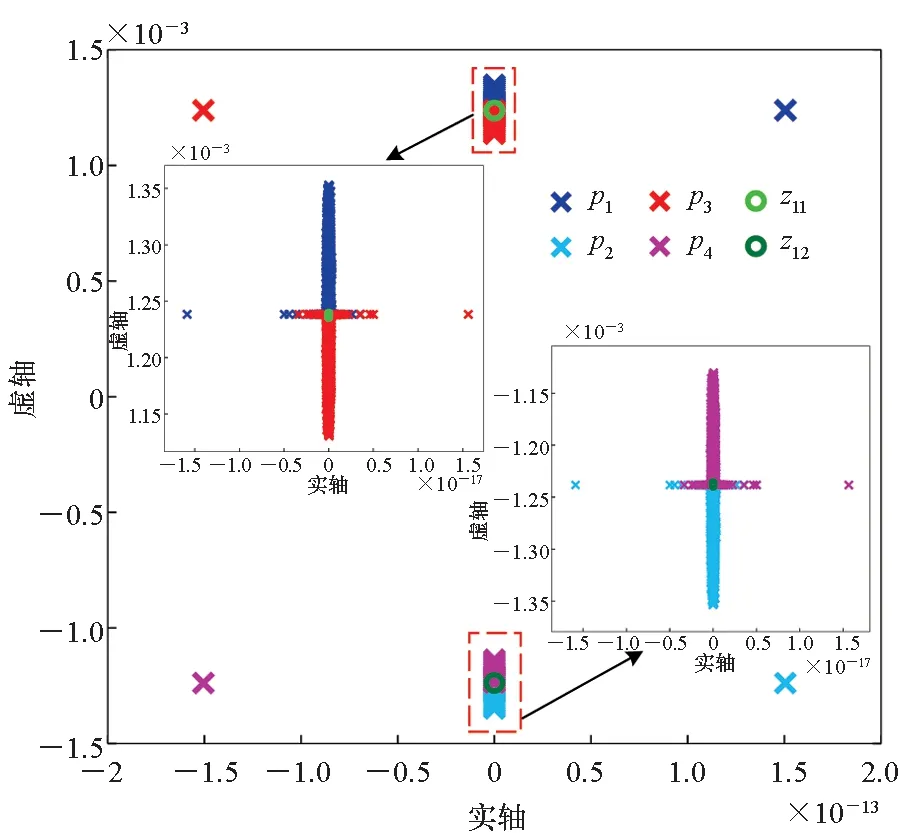
(b) 式(7)的零极点分布(b) Distribution of zeros and poles of Eq.(7)图3 东西方向运动的传递函数零极点分布Fig.3 Distribution of zeros and poles of transfer functions for east-west motion

图3给出了VE∈[-100 m/s,100 m/s]，L∈[0°,70°]时，传递函数式(6)和式(7)的零极点分布。从图3可以看出，传递函数式(6)和式(7)的零极点也分布在一个集中的范围，因此也可以选择任意一对东向速度和位置对应的传递函数的特征来代表整类运动模式下SINS水平姿态误差与水平重力扰动间的误差传递特征。

3 组合导航模式下的误差传递函数

当SINS工作在组合导航模式时，将陀螺漂移和加速度计零偏建模为常值项与随机项之和，用位置作为观测量，系统滤波模型为：

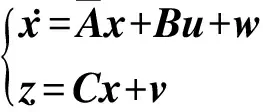
(8)

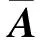
系统的输出方程为：

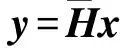
(9)

Kalman滤波模型能够得到x中能观状态的最优估计，并给出最优增益矩阵K。组合导航模式下，系统误差传递的结构如图4所示。

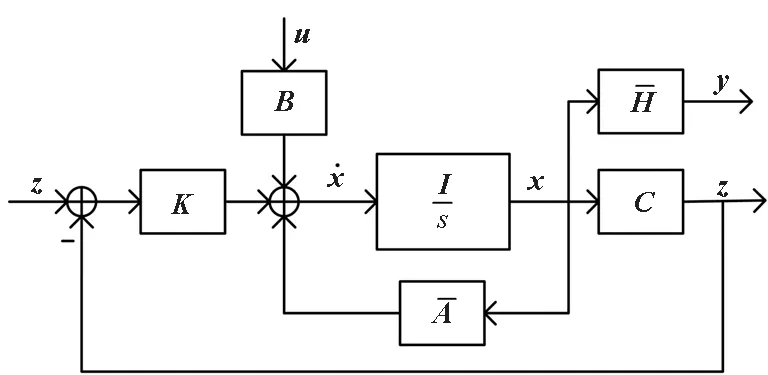
图4 组合导航模式下系统结构图Fig.4 Diagram of system under integrated navigation mode

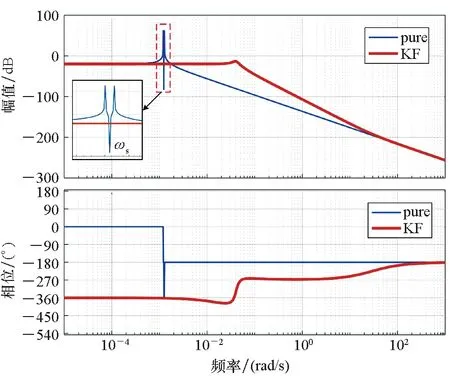
(a) φE/gdN

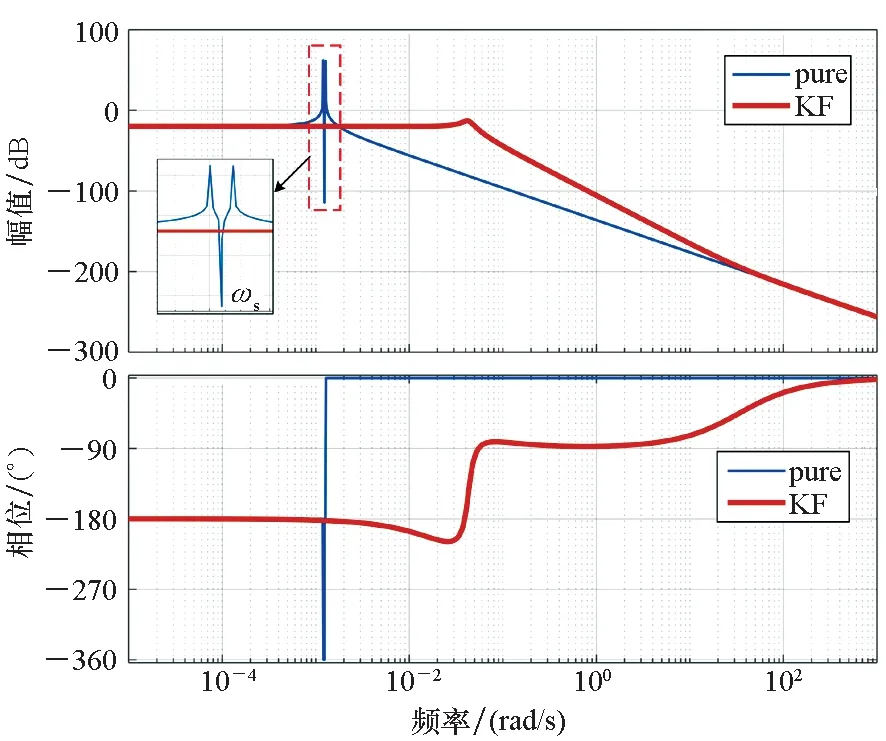
(b) φN/gdE图5 南北方向运动的传递函数Bode图Fig.5 Bode diagram of transfer functions for north-south motion

(a) φE/gdN

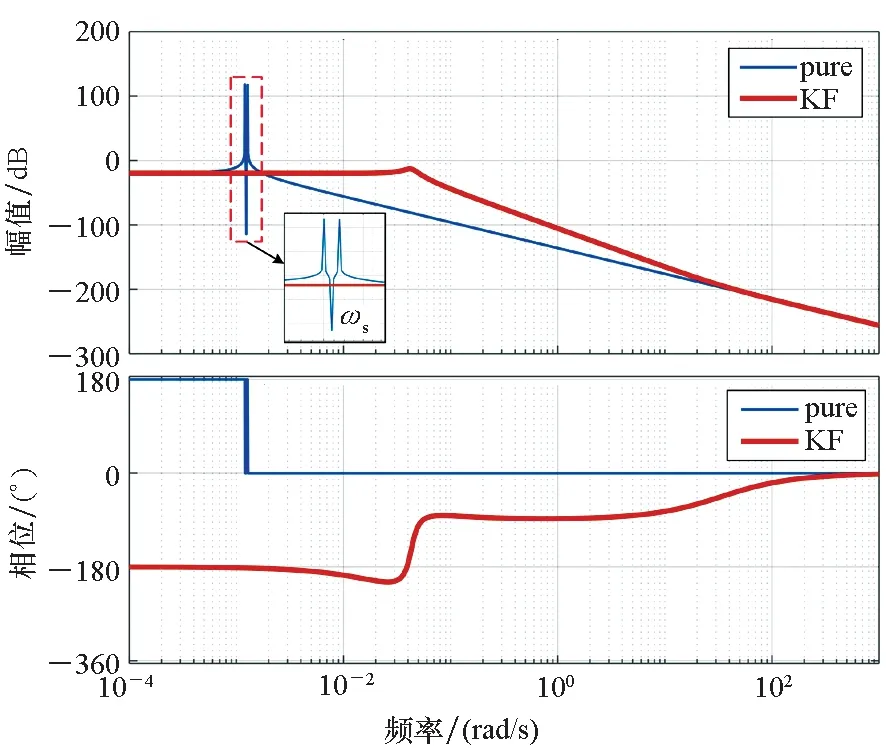
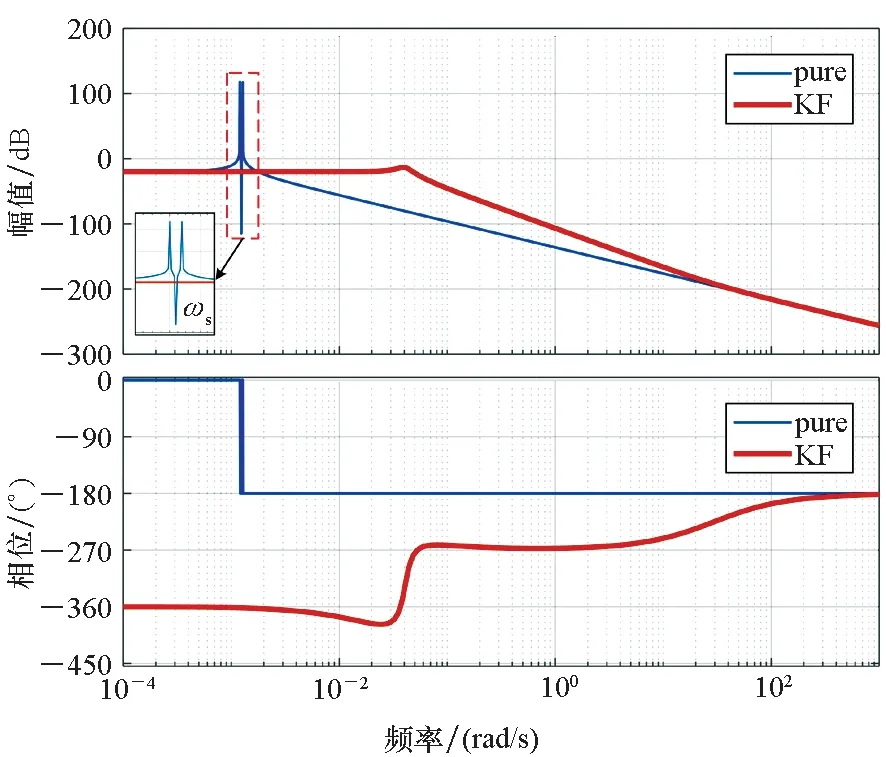
(b) φN/gdE图6 东西方向运动的传递函数Bode图Fig.6 Bode diagram of transfer functions for east-west motion

根据式(8)、式(9)和图4，系统输入输出间的传递函数为：

(10)

当没有Kalman滤波环节时，K为零矩阵，传递函数退化为纯惯性解算模式，如式(3)所示。比较式(10)和式(3)，可以看出，Kalman滤波器的引入改变了系统的基本模态，也会改变零极点分布。因此只分析纯惯性解算模式SINS水平姿态误差与水平重力扰动间的关系是不够的。

4 仿真及应用分析

由第2节的分析可知，当载体沿南北方向或东西方向匀速直线运动时，可以选择常用位置和速度范围内任意一组位置和速度下传递函数的特征来代表整类运动。因此，不失一般性，选择L=30°，VN=10 m/s代表南北方向匀速直线运动，选择L=30°，VE=10 m/s代表东西方向匀速直线运动。

当载体沿南北方向匀速直线运动时，绘制SINS水平姿态误差与水平重力扰动间传递函数的Bode图，如图5所示。图5中：蓝色曲线代表纯惯性解算模式(pure)，即传递函数式(4)和式(5)；红色曲线代表组合导航模式(KF)。

当载体沿东西方向匀速直线运动时，绘制SINS水平姿态误差与水平重力扰动间传递函数的Bode图，如图6所示。图6中：蓝色曲线代表纯惯性解算模式，即传递函数式(6)和式(7)；红色曲线代表组合导航模式。

从图5、图6可以看出，在纯惯性解算模式下，系统存在两个在ωs附近的自然频率。当水平重力扰动为常值时(如静基座情况下)，SINS水平姿态误差在重力扰动激励下表现为振荡运动，振荡频率约为ωs；当水平重力扰动的时间频率等于自然频率时，SINS水平姿态误差将在重力扰动的激励下振荡幅值达到最大。在组合导航模式下，Kalman滤波器相当于在系统中加入阻尼，同时增大了系统的截止频率，这意味着组合导航模式下，SINS姿态误差受更多高频重力扰动信号的影响。

将频率范围分成三个区间：当重力扰动信号的时间频率低于7×10-4rad/s时，SINS水平姿态误差与水平重力扰动间的传递函数近似为比例环节，如式(11)和式(12)；当重力扰动信号的时间频率高于0.05 rad/s时，传递函数的幅值急剧衰减；当重力扰动信号时间频率在7×10-4～5×10-2rad/s范围时，纯惯性解算模式下传递函数幅值以-40 dB/dec的速度衰减，组合导航模式下，传递函数相位存在滞后。

(11)

(12)

由于传递函数的自变量是时间频率，而重力扰动信号是空间相关量，通过载体运动，转换为时间频率信号作用于系统，转换关系如式(13)所示。

(13)

式中：ω为时间频率，v为载体运动速度，λg为重力扰动信号波长。

不同重力扰动信号波长对应的传递函数特性见表1。

表1 不同重力扰动信号波长对应的传递函数特征

对组合导航模式而言，当重力扰动信号波长λg<40πvs/rad时，不会对SINS姿态解算带来太大误差，可以不用补偿。当重力扰动信号波长λg≥40πvs/rad时，为了提高SINS的解算精度，需要补偿该波段的重力扰动。

比较两种解算模式，发现组合导航模式下，SINS姿态误差受更多高频重力扰动信号的影响，这意味着组合导航模式下的SINS需要更高分辨率的重力扰动数据来进行重力扰动补偿。由图5和图6看出，系统存在截止频率，这使得高于该频率的重力扰动信号不会作用于SINS的水平姿态。这就说明在对高精度SINS进行重力扰动补偿时，对于重力扰动分辨率的需求是有限度的，并不是越精细越好，因为过于精细的重力扰动数据一方面带来测量压力，另一方面带来存储压力，却并不会提高SINS的姿态精度。

5 结论

本文推导了载体匀速直线运动时，SINS水平姿态误差与水平重力扰动间的传递函数，在常用速度和位置范围内，传递函数的零极点分布非常集中。然后推导了组合导航模式下，SINS水平姿态误差与水平重力扰动间的传递函数，Kalman滤波器的引入会改变系统的基本模态，也会改变零极点分布。仿真中，分别用L=30°，VN=10 m/s和L=30°，VE=10 m/s代表南北方向、东西方向匀速直线运动，分析了纯惯性解算模式和组合导航模式下传递函数的幅频特性。组合导航模式下，SINS姿态误差受更多高频重力扰动信号的影响。组合导航模式下的SINS需要更高分辨率的重力扰动数据来进行重力扰动补偿。在对高精度SINS进行重力扰动补偿时，对于重力扰动分辨率的需求是有限度的，不是越精细越好，过于精细的重力扰动数据一方面带来测量压力，另一方面带来存储压力，却并不会提高SINS的姿态精度。