点邻域尺度差异描述的点云配准算法*
陆 军,陈 坤,范哲君
(1. 哈尔滨工程大学 自动化学院, 黑龙江 哈尔滨 150001;2. 哈尔滨工程大学 船海装备智能化技术与应用教育部重点实验室, 黑龙江 哈尔滨 150001)
随着Kinect、3D激光雷达和地面激光扫描仪等新型传感技术的发展,点云数据的获取越来越高效。三维点云数据处理技术也得以快速发展,并且在计算机图形学、CAD造型设计、文物古迹保护、汽车制造业等众多领域都有广泛应用。在点云获取时,点云采集设备因为广角不够,物体太大等问题,有时不能一次完整的得到整个点云数据,需要分多次采集点云,采集的点云之间有位移角度偏移,想要完整的点云就需要点云配准。3D点云配准是后续工作的基础和前提,是点云处理技术的一个重要组成部分。如何使点云配准方法更加快速准确已成为点云研究的热点和难点之一。
在点云配准的众多方法中,最经典且最常用的是迭代最近点算法[1]。迭代最近点(Iterative Closest Point, ICP)配准算法的核心方法是最小二乘法,由于它的强大功能和高精确度,得到了广泛的应用。但是,ICP算法也存在一些缺点:要求待配准的点云重叠面积大,容易得到局部最优的结果,初始位置偏差不能太大。为了更有效地进行点云配准,一些其他方法被提出,其中应用比较广泛的是基于特征描述符的点云配准方法。此类算法可以在不知道初始条件的情况下快速估算出一个转换平移矩阵。Zhong[2]通过建立局部参考坐标系和各点三维柱状图的方法,设计了固有形状特征来描述点特征信息,但点分布不均及测量噪声会对配准结果产生影响。Rusu等[3]提出了一种点特征直方图(Point Feature Histogram, PFH)算法和一种快速点特征直方图(Fast Point Feature Histogram, FPFH)[4-5]算法作为局部特征描述符。PFH和FPFH根据从相邻点集获取的特征信息为每个点生成特征直方图。局部二进制模式(Local Binary Patterns, LBP)[6]和方向特征直方图(Signature of Histograms of OrienTations, SHOT)[7-8]也是常见的特征描述方法,但LBP算子特征信息的描述过于单一,SHOT算子纬度高、计算复杂。Jiao等[9]提出结合尺度不变特征变换(Scale Invariant Feature Transform, SIFT)和ICP的点云配准算法,提高了配准精度。王畅等[10]提出了一种基于点云结构特征的快速配准算法,用以解决数据点缺失、点云散乱时的配准问题。Li等[11]提出了从全景图像和点云语义特征提取的自动配准方法。Lin等[12]提出结合固有形状特征(Intrinsic Shape Signature, ISS)算法的特征提取方法,提取的特征具有尺度不变性。
为了减少特征描述的计算量,本文提出一种点邻域尺度差异描述的配准算法。该算法利用拟合曲面的形状指数随曲面形状变化的特性,选取局部拟合曲面变化大的点为关键点,提取的关键点在点云中具有一定的代表性。通过对关键点选取不同的邻域空间提取特征信息,将这些特征信息组合成特征描述符,称为点邻域尺度差异描述符。该描述符具有计算简单、辨识能力强的优点。最后通过对应点对二重筛选和全局最优查找,有效地筛除了错误的对应点对,提高了点云配准的效果。
1 点邻域特征差异描述配准算法
本文提出了一种点邻域尺度差异描述的点云配准算法。主要有以下几个步骤:基于形状指数的关键点选取方法、点邻域尺度差异描述符的建立、对应点对二重筛选及最终变换矩阵的确定。
1.1 基于形状指数的关键点选取
1.1.1 曲率计算
曲率是描述曲面的弯曲程度的概念,是曲面的一个基本属性。点云是大量离散点的几何,描述真实物体的表面轮廓。在点云处理过程中,曲率同样是描述点云几何特性的一个重要属性。通常情况下,点云中的每个点和其邻近的点都可以拟合成一个局部的曲面,用局部曲面曲率作为点云中该点的曲率。本文使用最小二乘法进行曲面拟合[13],得到离散点邻域的局部曲面参数方程z=r(u,v)。通过得到的离散点所拟合的曲面,可以计算出高斯曲率K和平均曲率H。计算公式可见式(1)和式(2)。其中,E、F、G和L、M、N分别为二次参数曲面的第一类基本量和第二类基本量。
(1)
(2)
由上式可以计算得到曲面的最大主曲率k1和最小主曲率k2:
(3)
(4)
其中:E=ru·ru;F=ru×rv;G=rv×rv;L=ruu·n;N=rvv·n;M=ruv·n;ru、rv、ruu、rvv、ruv为拟合曲面的偏微分;n是曲面的单位法向量。
1.1.2 关键点选取方法
Dorain和Jain[14]提出了一个能够定量描述曲面的形变状态的量,称之为形状指数。形状指数的定义如式(5)所示。
(5)
式中:p为曲面上的一点;k1和k2分别表示包含点p的曲面的最大和最小主曲率。
由式(5)中的定义可以看出,形状指数S的取值范围为[0,1],可以将曲面特征用0到1的数值表示,k1、k2分别为曲面的最大、最小曲率,如式(3)所示。形状指数是用来表示曲面形状的,形状指数的大小随着曲面的变化而变化。
通过形状指数的性质可知,如果点云中某一点的用于描述其局部曲面特征的形状指数与其附近点的形状指数相差很大,则可以判断出该点周围的曲面变化剧烈。通常曲面中的这种点在点云中有很强的代表性和可区分性,适合被选作关键点。
分别在源点云和目标点云中找出形状指数变化大的点作为关键点。对于点云中的每一点p,当满足式(6)或式(7)中任一条件时,可将其选为关键点:
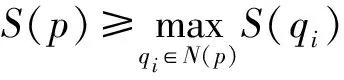
(6)
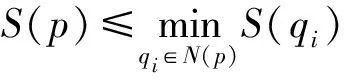
(7)
(8)
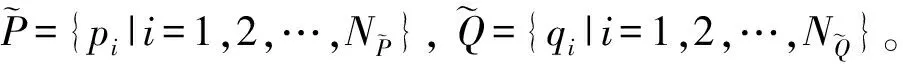
1.2 点邻域尺度差异描述符
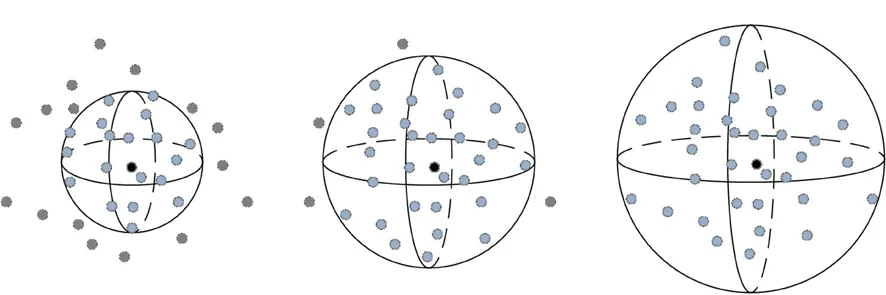
针对获得的关键点,本文设计了根据点邻域尺度差异得到的特征描述符。首先对关键点集中的每一点建立局部参考坐标系,然后根据局部几何信息,获得其特征信息。图1为点云中不同尺度的邻域空间示意图,用黑色标记关键点,蓝色标记邻域点,灰色标记无关点。如图1所示,对同一关键点,不同尺度的邻域空间的邻域点分布各不相同,因此建立的局部坐标系也会存在差异,同时在不同局部坐标系下的相同类型的特征信息同样会存在差异。这样,通过不同尺度的点邻域空间信息描述关键点特征,扩大了描述关键点信息的空间范围,提高关键点描述的显著性和计算效率。下面介绍具体的计算过程:
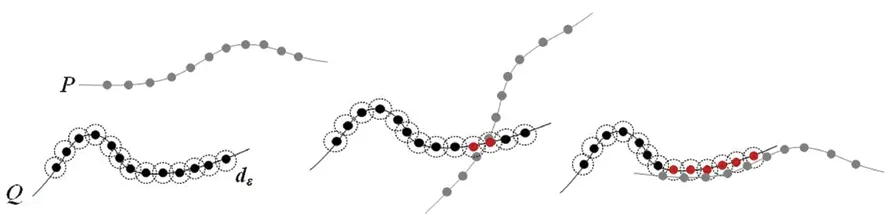
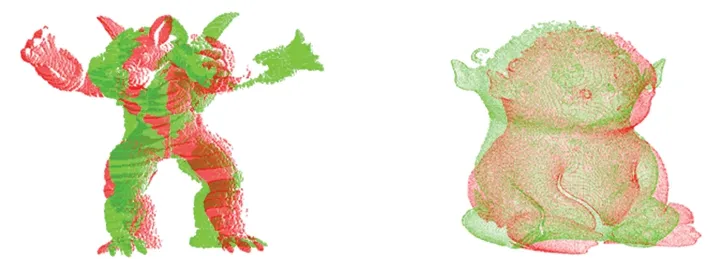
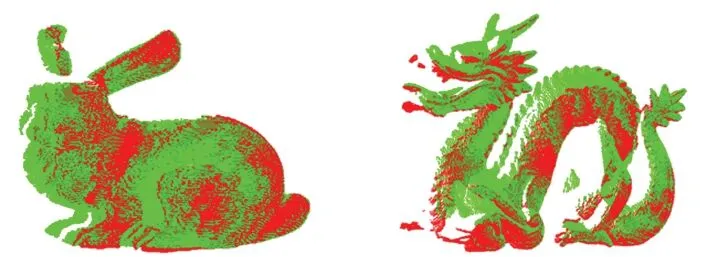
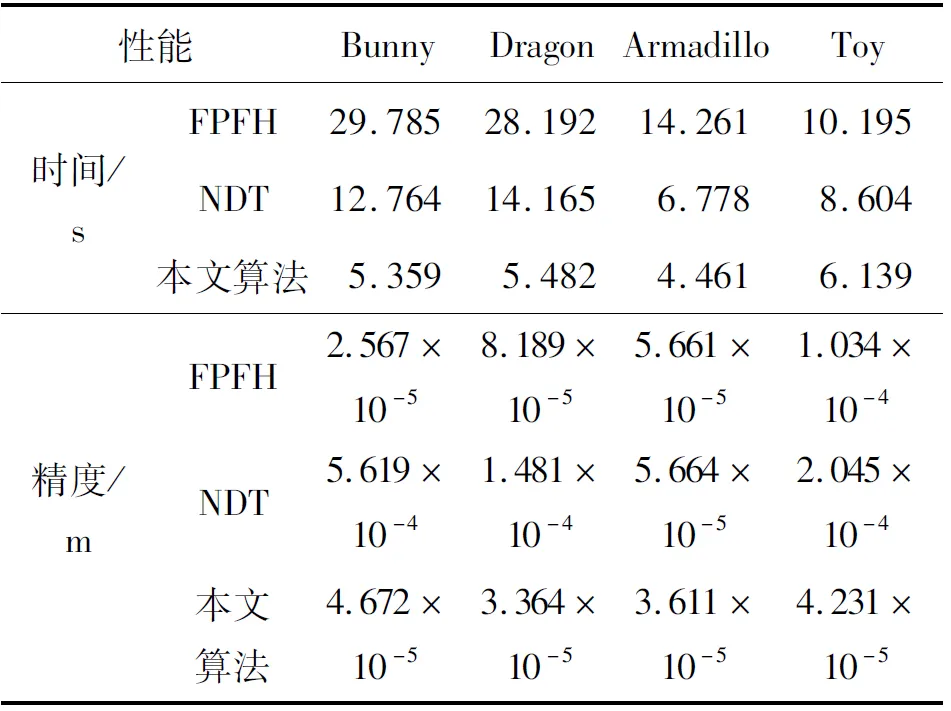
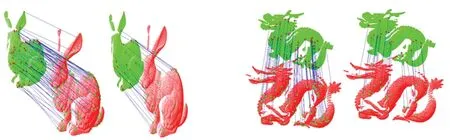
对于采样点p,取l个大小不同的邻域半径,相邻邻域半径之差为Δr,有r1 (9) 在局部参考坐标系建立的过程中,传统方法受点云密度分布和噪声点的影响较大,建立的局部坐标系不准确,还会导致依据局部坐标系计算的法线等几何信息不准确。为了改善这个问题,在求协方差矩阵过程中,引入关键点与其邻域点的欧式距离作为权值,如式(9)所示,邻域中各点与关键点的距离的不同对协方差矩阵的构建产生不同的影响,距离越近,影响越大。这样的加权方法能够有效地抑制外围噪声和杂波的干扰。图1中灰色无关点对局部参考坐标系的影响将大大降低。 图1 点云中不同尺度的邻域空间Fig.1 Neighborhood spaces of different scales in point clouds 特征值{λl1,λl2,λl3}(λl1>λl2>λl3)和对应的特征向量{vl1,vl2,vl3}可由式(9)所求得的Cl进行奇异值分解得到。将三个特征向量作为三个坐标轴,建立关键点的局部坐标系。特征向量vl1、vl2对局部邻域中邻域点密度变化敏感,但是特征值之和与特征向量vl3具有很强的旋转不变性,局部稳定性高[15],所以基于特征值λl1、λl2、λl3和特征向量vl3建立局部描述符。由于本文是通过欧氏距离加权的方式求取的协方差矩阵,所以所求得的特征向量vl3与传统方法所求的特征向量存在差异,但是其仍然具有良好的局部稳定性,而对点的局部描述符的建立与该描述符是否具有现实的几何意义无关,因此这不会影响到vl3对关键点的描述性,下文称vl3为法向量。 本文设计的多尺度特征描述符向量由两部分组成: 1)根据特征值{λl1,λl2,λl3}和对应的特征向量{vl1,vl2,vl3}构建特征值归一化向量hl: (10) 当用于建立局部坐标系的邻域半径改变时,通过式(9)求得的协方差矩阵也会不同,奇异值分解出的特征值也会改变,式(10)所求的hl则会发生变化,此时可以将不同邻域半径下的特征值归一化向量hl的差值作为局部特征描述符的一部分特征。不同邻域半径所求得的特征值归一化向量hl的差值分别为Δhk=Δhk+1-Δhk(k=1,2,…,l-1),随后得到一个3l-3维的向量H: H=(Δh1, Δh2, …, Δhl-1) (11) 2)法向量之间的夹角余弦。对每个关键点,不同邻域半径下所求得的特征值不相同,该点在不同尺度邻域空间的法向量也不同,这些法向量之间的夹角同样可以作为点邻域尺度差异描述符的组成部分。 首先,选取l个互异的邻域半径值,通过求协方差矩阵,奇异值分解等步骤得到l个法向量n1,n2,…,nl,计算不同邻域空间的法向量之间的夹角余弦值为: (12) 将计算得到的l-1个法向量夹角余弦值αi组合为一个l-1维的向量N: (13) 综上,不同邻域半径下所求得的特征值归一化向量hl的差值组合为H,法向量夹角的余弦值组合为N,将H和N组合为一个4l-4维的向量F作为点邻域尺度差异描述符: (14) 由于点云模型可能是对称的,或者局部多处高度相似,上文中得到的对应点对集E中可能存在错误的点对,如果只用特征描述符向量的欧式距离查找对应点对,得到错误的对应关系的概率很大,并且传统的随机采样一致性(RANdom SAmple Consensus, RANSAC)算法在输入样本集高度相似的情况下也很难避免这种错误。故本文设计了一种基于全局距离的全局优化算法,能够有效地剔除上述情况带来的错误对应点对。 定义两点云之间的全局距离为: (15) (a) 远离(a) Faraway (b) 相交(b) Crossover (c) 接近(c) Approach图2 两点云相对位置情况示意图Fig.2 Relative position of two point clouds 利用上述方法得到的全局距离D(P,Q),提出了对应关系全局优化算法,以求取最终旋转变换矩阵,具体过程如下: 令P表示源点云,Q表示目标点云,对应关系构成的集合为E={e1,e2,…,en},从E中随机抽选n(n≥3)组对应关系,计算变换矩阵Ti,利用Ti将源点云P变换到新的坐标系PT,利用式(15)获得D(PTi,Q)。选取合适的阈值Dε,当D(PTi,Q) 本小节通过设计实验来验证本文算法的可行性和有效性。本文实验均是在Windows 7 64位操作系统下,使用C++语言实现。实验所用PC机配置为Intel(R) Core(TM) i5-4210M处理器,物理内存为8 GB。实验所用点云为3个斯坦福大学点云模型库中双视角扫描点云数据Bunny、Dragon和Armadillo,实验室设备采集点云Toy。这四组点云中,源点云和目标点云的采集视角差各不相同,分别为45°、48°、60°和45°,图3展示了4组点云配准前的初始位置,其中用绿色点标记的点云为源点云,用红色点标记的点云为目标点云。 (a) Bunny (b) Dragon (c) Armadillo (d) Toy图3 四组点云配准前初始相对位置Fig.3 Initial relative positions of four sets of point clouds (a) Bunny (b) Dragon (c) Armadillo (d) Toy图4 四组点云的基于形状指数的关键点分布Fig.4 Key point distribution of four point clouds based on shape index (a) Bunny (b) Dragon (c) Armadillo (d) Toy图5 四组点云数据配准结果Fig.5 Registration results of four sets of point cloud data 本文通过基于形状指数的方法对图3四组点云提取关键点。图4所示为四组点云的关键点分布情况,其中关键点为蓝色。 由图4可知,源点云和目标点云中的关键点分布很相似,说明找到的关键点具有很强的代表性,有助于接下来的对应关系查找。同时,可以看到提取的关键点在整个点云中分布均匀,为局部区域中特征突出的点,能够代替整个点云完成接下来的点云配准。 采用本文提出的配准算法对四组点云进行配准实验。由四组待配准点云得到的最终配准结果如图5所示。从图5中可以看到,四组数据中的源点云和目标点云基本重叠在一起,配准效果良好。表1展示了本文配准算法与基于快速点特征直方图的点云配准算法和正态分布变换算法(Normal Distributions Transform, NDT)在四组点云的配准精度和时间。通过对比可以看出,本文算法与两种配准算法相比较配准精度更高,且消耗的时间更短。 表1 点云配准算法时间精度对比 实验中对邻域半径进行手动调节,通过多次试验,最终将邻域半径r设定为0.003 m来进行点云曲率、法向量估计及特征描述符建立。 为了验证参数a,b对关键点提取的影响,设计实验进行验证,结果如图6所示。对比图6中第一行点云(源点云),图6(b)中a和b都为0,可以看出关键点密度较大。当a或b增大时,如图6(a)和图6(c)所示,关键点数量减少。从图6(b)可以看出,源点云和目标点云中的关键点分布情况基本相同,重叠区域存在大量关键点,关键点选取方法效果较好。 (a) a=1,b=0 (b) a=0,b=0 (c) a=0,b=1图6 不同a和b值下的关键点分布Fig.6 Distribution of key points with different parameters a and b 表2列出了参数a和b不同取值下的关键点个数。Bunny点云(源点云和目标点云)初始个数分别为40 256、40 097,表2列出了6组关键点个数。从第2、3、4、7列可以看出,随着参数a和b的增加,关键点个数有明显减少,但a和b都为1时,两点云关键点个数分别只有2、3。从第2、5、6列可以看出,单独增加a、b值同样会减少关键点个数。 表2 不同参数a, b下的关键点个数 设计实验验证1.3节中的对应关系查找算法的效果。通过对比候选对应点集和对应点对二重筛选算法得到的对应点集进行分析,对比效果图如图7所示。图7中每组图中包含候选对应点对(左图)和对应点对二重筛选算法得到的对应点对(右图)。从图7中可以看出每组图中左图都比右图多出许多错误对应点对。在图7(a)中,左图为基于欧式距离最近原则确立的候选对应点对图,共有84对对应关系,右图为本文二重筛选算法得到的对应点对结果,共有24对,从图中可以看出对应关系准确且均匀。同样地,在图7 (b)~(d)中,左图分别有90、85、112对对应点对,明显可以看出其中有一些错误对应关系,右图分别为本文二重筛选算法筛选出的27、29和51对对应点对,基本上剔除了错误对应,对应点对的分布也比较均匀,有利于最终配准效果的提高。 (a) Bunny (c) Dragon (c) Armadillo (d) Toy图7 候选对应点对集与最终对应点对集分布Fig.7 Distribution of candidate correspondence point pair set and final correspondence point pair set 设计了一种点邻域特征差异描述的点云配准算法。首先根据拟合曲面的形状指数随着曲面的形状变化而变化的特性,选取局部拟合曲面变化大的点为关键点。然后,对于每个关键点,将不同邻域半径下所求得的特征值归一化向量的差值和法向量夹角的余弦值组合为点邻域尺度差异描述符。最后,在基于欧式距离的对应点查找方法的基础上,提出了对应点对二重筛选及全局优化算法,提高了对应关系的准确率。实验证明本文配准算法的配准速度快,计算效率高,同时配准精度高,具有很强的噪声鲁棒性。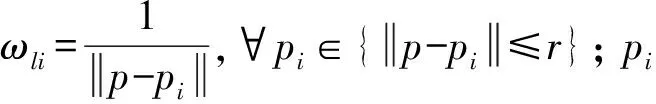
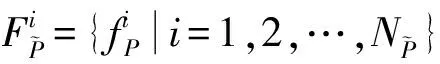
1.3 对应关系二重筛选及全局优化算法

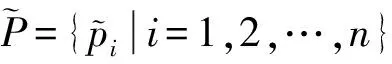
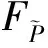
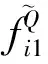
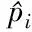

2 实验结果分析




2.1 关键点提取
2.2 配准实验
2.3 参数a, b对关键点分布的影响


2.4 对应关系查找

3 结论

