三角翼机翼摇滚主动控制多学科耦合数值模拟

杨起，刘伟，杨小亮，李昊

国防科技大学 空天科学学院，长沙 410072

飞行器大攻角飞行时，非定常分离和非对称旋涡主导了周围流场，所受气动力/力矩具有非线性和非定常性的特点。由此，产生了包括机翼摇滚(Wing Rock)在内的多种飞行器动态稳定性问题。机翼摇滚涉及气动、运动及控制等多门学科，影响飞行器机动能力。严重的摇滚问题将引起战斗机纵向以及横航向耦合的动态问题，使飞行器进入危险的深度尾旋状态，严重威胁飞行器的飞行安全。因此，对飞行器摇滚机理和控制手段的研究是十分必要的。

针对摇滚问题，国内外进行了大量的数值模拟和试验研究，对摇滚现象及其机理有了深入的认识[1-2]，并开展了对飞行器滚转运动控制方法的研究。基于机翼摇滚动力学模型，采用经典理论、神经网络、状态观察器等方法所设计的控制律[3-5]能有效地抑制动力学模型描述的振荡运动。上述研究重点关注了控制算法，采用拟合的数学模型来描述飞行器的耦合效应。然而，所采用的拟合模型是对数值模拟结果的简化，且仅将控制系统视为一个后增的设计，实际上并没有考虑控制系统和气动/运动的耦合作用，相关研究并不能作为评估三角翼摇滚控制系统性能的可靠手段。为了充分考虑三角翼动态运动中非线性、非定常的多学科耦合效应，提高控制系统设计精度，需要将气动、运动和控制系统耦合计算，优化飞行器控制律。

目前，三角翼机翼摇滚气动/运动/控制多学科耦合效应的研究尚处于初步探索阶段。喷流不仅能直接提供控制力和力矩，而且能通过改变飞行器周围流场提供间接的控制力和力矩，是一种常见的控制手段。Cummings[6]和Riou[7]等研究了前缘喷流对背风面流场的影响，发现前缘喷流可以影响主涡位置、涡破裂、二次分离涡和剪切层的相互作用。Kandil等[8]从数值上分析了采用翼面差动喷流控制三角翼摇滚的可行性，发现采用前缘非对称喷流，可以产生相应的滚转控制力矩。同时，受推力矢量技术的影响，1994年Helin和Watry[9]对后缘喷流展开了试验研究，他们发现后缘喷流对外部压力梯度进行了修正。在大迎角情况下，后缘喷流可使60°后掠三角翼非对称涡的出现得以推迟，这有利于克服机翼摇滚现象。Nawrocki[10]研究了不同喷流方式(对称喷流、差动喷流和矢量喷流)对前缘涡的影响，发现在大攻角的情况下，射流有控制背风面涡流的作用，能推迟涡破裂的产生。国内，王晋军[11]、阎超[12]等也分别进行了后缘喷流的试验和数值模拟研究。然而，上述研究都仅关注了喷流在涡流控制方面的应用，数值模拟也仅局限于Navier-Stokes(N-S)方程的求解，不涉及运动、控制领域。Kandil等[8]虽然对三角翼摇滚的喷流主动控制过程进行了数值模拟，但仅仅是将喷流作用简化为刚体动力学方程组中的阻尼项，并未考虑喷流与动态流场的相互作用，不能精确模拟三角翼在喷流作用下的运动特性。相关的多学科耦合技术虽然被成功地应用于返回舱俯仰运动的控制方法研究中[13]，但在三角翼摇滚运动中的应用还局限于喷流对背风面涡流的影响，不涉及气动、运动和控制的耦合效应。

控制面偏转是另一种控制手段。前缘控制面利用背风面涡流对三角翼前缘敏感的特点[1]，通过偏转改变前缘形状和位置，提供一定的控制力矩。其中振荡的前缘可视为一个涡量的非定常来源，以调控背风面的涡量[14]。Lee和Batina[15]基于锥形流假设的Euler方法，对采用前缘差动手段的滚转控制过程进行了数值模拟，在20°攻角下实现了三角翼摇滚的有效控制。Walton和Katz[16]在风洞试验中验证了采用前缘襟翼差动振荡机构控制双三角翼摇滚的可行性：将超过 20°的滚转振幅控制在 5°以下。Deng和Gursul[17]研究了前缘襟翼的非定常振荡对三角翼背风面涡及涡破裂的影响，发现涡破裂位置受襟翼振幅和攻角的影响，呈迟滞变化。Boelens等[18]数值模拟了带中心体65°后掠三角翼的自由滚转运动。通过预先设定后缘副翼差动运动规律，研究了在马赫数0.5、17°攻角条件下的滚转运动特性，并比较了不同求解器的结果，验证相关数值方法的可行性。Schütte等[19]利用求解器TAU数值模拟了带中心体的三角翼后缘副翼差动至5°时滚转运动情况，并与试验结果进行了对比。此研究虽然局限于耦合方法的验证，但展示了后缘副翼差动对背风面涡流及背风面吸力峰值的影响。此后，该研究团队进一步通过数值模拟研究了后缘副翼开环运动(预先设定控制面运动规律)的控制效果[20-22]。李喜乐和杨永[23]进一步拓展了Boelens的工作，在数值模拟中考虑了由副翼差动产生的副翼与飞行器间缝隙的影响。目前可动部件控制手段的研究虽涉及了三角翼气动、运动和控制的耦合作用，但多是开环控制的情况。闭环控制数值模拟中，文献[15]虽然实现了采用前缘差动的三角翼滚转运动闭环控制的数值模拟，但所采用的Euler方法存在不能模拟二次分离和涡破裂现象的局限性，数值模拟结果精度受限。

总之，目前采用气动/运动/控制多学科耦合方法开展三角翼摇滚控制的研究十分少见。本文针对三角翼摇滚控制问题，基于RBF_TFI网格变形技术，通过耦合求解N-S方程、刚体滚转动力学方程和经典控制律，对采用后缘控制面差动偏转的摇滚主动控制过程进行了多学科耦合数值模拟，研究了控制器不同控制状态的控制效果，为三角翼摇滚运动主动控制的多学科耦合效应研究建立基础。

1 多学科耦合数值模拟方法

1.1 控制方程及离散方法

流场控制方程为计算坐标系下的三维非定常无量纲N-S方程(式(1))，采用无量纲单自由度Euler方程模拟三角翼滚转运动(式(2))，并基于经典控制理论设计控制器(式(3))：

(1)

(2)

(3)

式中：φ为滚转角；Cl_all为三角翼所受总的滚转力矩；δ为控制面差动偏转角；t为无量纲时间。假设控制面无厚度，控制面偏转对质心处惯量张量无影响，因此其质心处的惯性张量Ixx不变。控制器为比例微分控制器，以滚转角及其角速度为反馈信号，反馈控制量为控制面差动偏转角，比例系数和微分系数分别为kP、kD。基于有限体积方法，采用二阶精度的Roe格式离散对流通量。采用中心差分格式离散黏性通量。采用含双时间步的LU-SGS方法进行时间推进求解，同时采用单边差分时间二阶精度格式离散滚转动力学方程。通过耦合求解3个方程，实现三角翼主动控制过程的数值模拟，基本步骤如图1 所示。

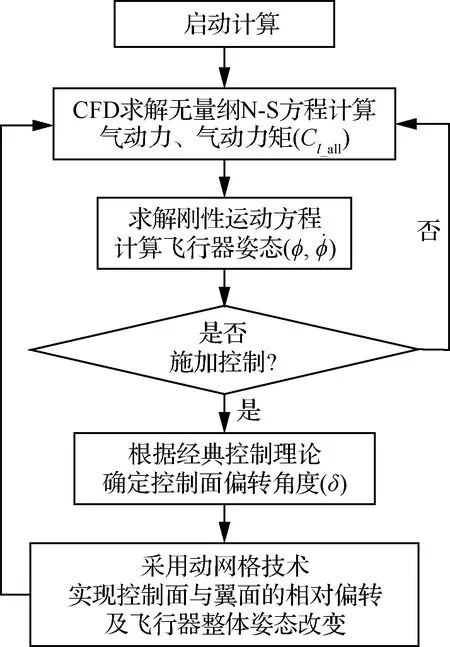
图1 三角翼主动控制过程

1.2 动网格技术及几何守恒律

采用刚性动网格技术实现三角翼整体滚转运动，采用RBF_TFI网格变形方法实现控制面偏转，结合两种动网格技术保证三角翼滚转及控制面偏转时的网格质量。RBF_TFI网格变形方法结合了径向基函数(Radius Basis Function，RBF)方法和超限插值(TransFinite Interpolation，TFI)方法的优点，是一种高效的网格变形方法[24]。其主要思路为：物面精确变形，精简径向基函数基点，利用径向基函数插值方法计算网格棱线的位移，然后通过超限插值方法获取面、体网格对应位移，从而实现整个计算域网格的变形。为避免大变形情况下出现网格交错的情况，需根据物体变形和网格划分情况添加基点数，提高边界处变形后的网格质量。

网格变形会引起流动方程数值计算时间精度的降低，本文考虑了几何守恒律[25]的影响，采取与流动方程相同的时间、空间离散方法离散GCL(Geometrically Conservative Law)方程[26]，通过DGCL(Discrete GCL)计算n+1时刻的网格体积。相关数值模拟结果证明，此方法能保持流动方程数值模拟的二阶时间精度[26]。

2 三角翼单自由度滚转运动数值模拟

采用刚性动网格技术分别对有/无后缘控制面的三角翼的自由滚转运动进行数值模拟。将无控制面三角翼自由滚转数值模拟的结果与文献[1-2]进行对比，验证本文所采用的数值方法。对比有/无控制面的三角翼数值模拟的结果，研究控制面对三角翼滚转运动特性的影响。

带控制面的计算模型为有厚度的80°后掠平板三角翼，控制面紧贴三角翼后缘，尺寸如图2(a)所示。以三角翼根弦长为参考长度，则三角翼无量纲转动惯量Ixx=0.1。而无控制面模型则没有后缘控制面，其余参数与有控制面模型相同。以三角翼顶点为坐标原点，建立体坐标系。从三角翼后缘向顶点看去，左控制面下偏、右控制面上偏时，控制面的偏转角为正，反之为负(图2(b))。采用O-H结构网格离散三角翼周围流场，流向、周向和法向分别分布201、181、75个网格点。在三角翼前缘和物面附近适当加密网格，并对三角翼控制面表面网格进行细化，壁面第1层网格法向尺度设为5×10-5倍根弦长度(图2(c))。来流马赫数Ma=0.3，基于根弦长的雷诺数为Re=4×104，在计算过程中三角翼基于根弦长的名义攻角不变,α=30°。

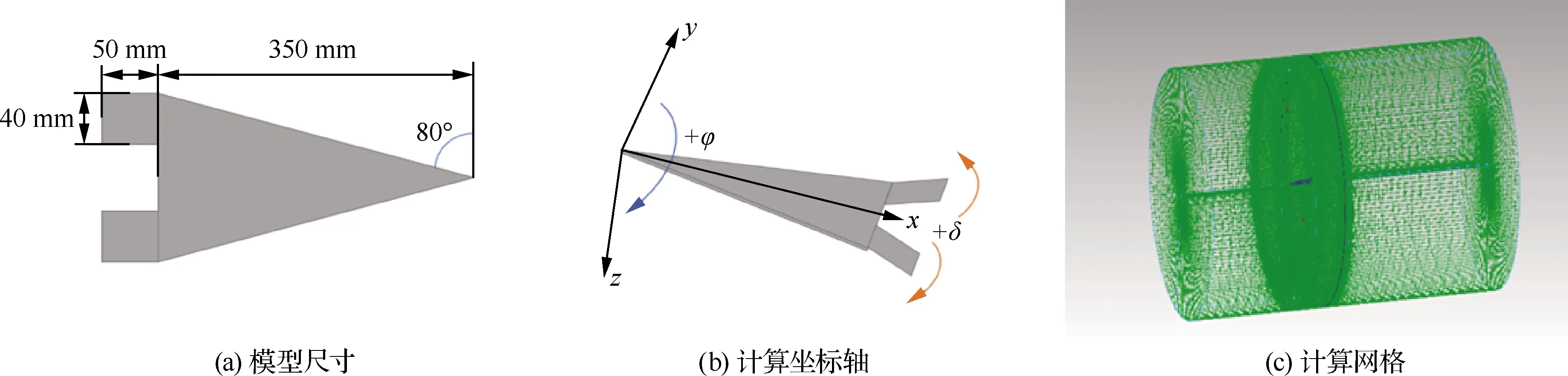
图2 带控制面三角翼计算模型及网格

图3展示了两类三角翼(是否带有控制面)单自由度滚转运动(控制面与翼面无相对运动)的数值模拟结果。两类三角翼模型均产生了自激摇滚现象：无控制面三角翼模型摇滚振幅大于30°，有控制面模型摇滚振幅大于40°。位于三角翼后缘两侧的控制面增加了三角翼的受力面积，背风面非对称涡产生了更强的滚转力矩使得三角翼更快地失稳达到摇滚状态，因此带控制面模型摇滚振幅更大，振动频率变快。国内外针对80°后掠三角翼进行了大量的单自由度摇滚试验和数值模拟。刘伟[2]采用网格数为73×77×47(流向×周向×径向)的网格成功模拟了三角翼单自由度自由滚转运动，并说明此种网格密度从定性角度研究机翼受扰后的自由滚转运动特性是可行的。在试验方面，虽然模型加工、转动惯量等细微差别导致摇滚振幅和频率有所差异，但相关研究结果在定性程度上是基本吻合的，三角翼摇滚振幅大于30°。因此，本文数值模拟结果从定性上和量级上是可信的。

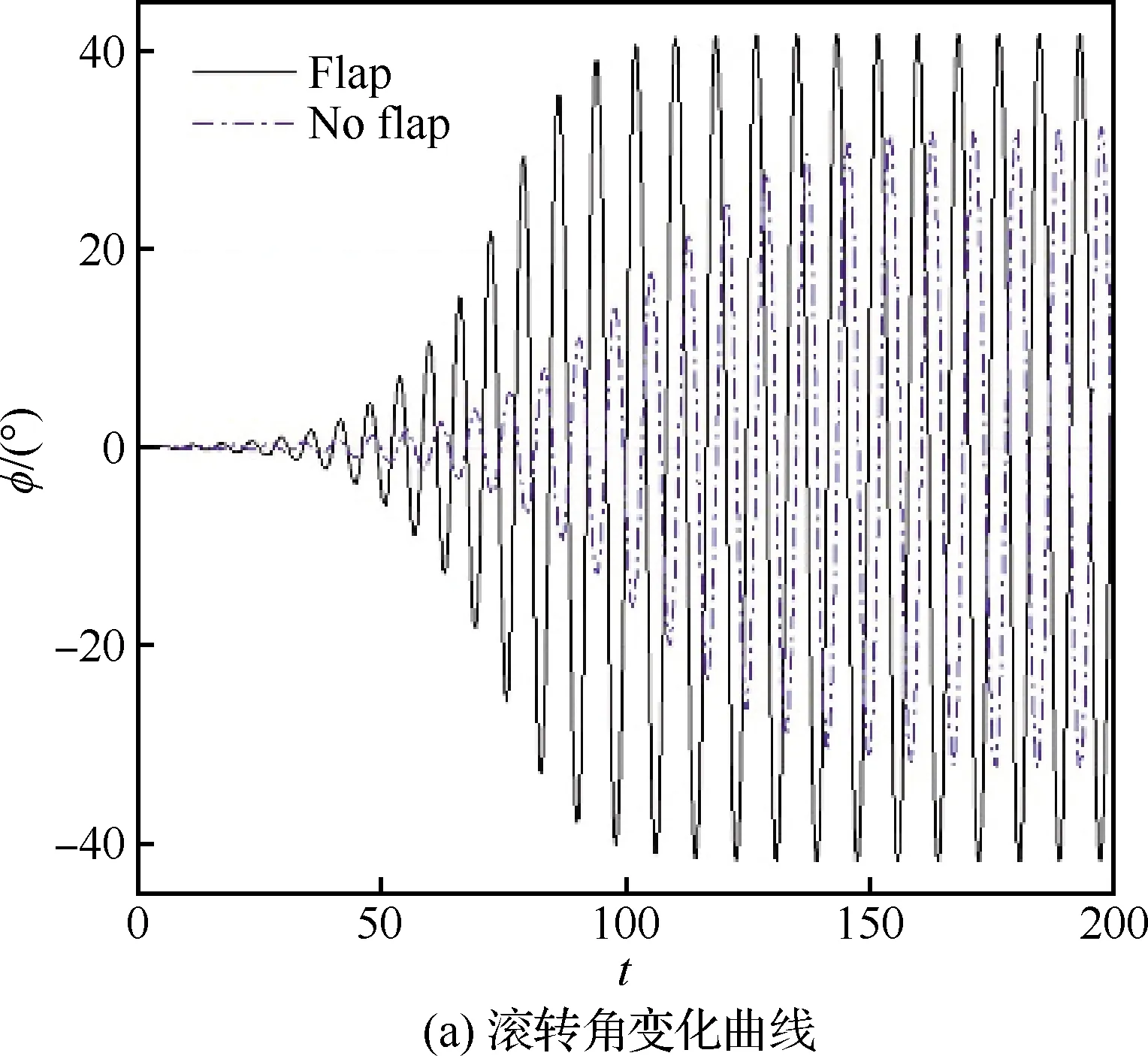
图3 三角翼单自由度自激滚转运动曲线

3 带控制面三角翼闭环控制线性模型

设计控制系统需建立三角翼受控滚转的运动模型。由于摇滚非线性问题的复杂性，同时受制于非线性动力学的发展，国内外还没有形成对摇滚机理的一致认识[2]，无法建立精确的三角翼摇滚运动模型。一种可行的办法是，根据数值模拟结果拟合出一个运动模型。此运动模型的精度受限，不能准确反映三角翼在控制系统作用下的运动特性，但能帮助确定控制系统参数范围。

假设三角翼受力是其状态参量及其一阶量的函数，建立三角翼闭环控制动力学模型。三角翼滚转时，可将控制面相对翼面的偏转运动视为扰动，则总的滚转力矩可分解为没有控制面偏转时由三角翼滚转运动引起的滚转力矩Cl_roll以及由控制面偏转运动产生的滚转力矩增量ΔCl_flap(式(4))。最终所受力矩可表示为滚转角、滚转角速度和控制面偏转角、偏转角速度的线性组合：

Cl_all=Cl_roll+ΔCl_flap

(4)

(5)

根据第2节中三角翼自由滚转的数据，经多重回归分析可求得参数a、b。

为了确定滚转力矩增量与控制面偏转角和偏转角速度的关系，对控制面正弦差动运动(δ=δAsin(kt)，δA为控制面偏转振幅；k为无量纲减缩频率;t为无量纲时间)进行了数值模拟，结果如图4所示。不同偏转角振幅下，滚转力矩随控制面偏转角迟滞变化，曲线形状相似，大小不同。控制面振幅为30°时，控制面动态偏转所能提供的最大滚转力矩超过了三角翼自由滚转最大滚转力矩的50%。控制面动态偏转能提供一定的控制力矩控制三角翼的滚转运动。由多重回归分析求得参数c、d。具体数值见表1，结合式(2)和式(3)得到三角翼闭环控制的运动模型：

图4 不同偏转角振幅下滚转力矩随控制面偏转角变化曲线

(6)

(7)

表1 气动模型参数

表2 不同控制状态的控制参数和系统阻尼比

为精确分析三角翼在控制系统作用下的运动特性，需对三角翼主动控制过程进行多学科耦合数值模拟。

4 带控制面三角翼摇滚主动控制数值模拟

基于建立的数值模拟平台，采用不同控制参数(C1～C6控制状态)，在极限环最大滚转角附近启动控制系统，对三角翼摇滚运动的主动控制过程进行多学科耦合数值模拟。采用与三角翼单自由度自激滚转运动数值模拟相同的计算模型和计算网格。其中控制状态C1～C3的微分系数为零，控制器为比例控制器。控制状态C4～C6，控制器为比例微分控制器。

比例控制器作用下三角翼滚转运动的数值模拟结果如图5 所示。在C1～C3控制状态下，三角翼受控后滚转角有一定减小，并进入频率加快的等幅振荡状态；后缘控制面的偏转角也随滚转角的减小而减小，最终等幅振荡。当三角翼进入稳定的等幅滚转振荡运动状态后，其所受滚转力矩与滚转角曲线呈 “双8”字型：在滚转角较小时，气流对三角翼做正功，曲线顺时针变化；滚转角较大时，气流对三角翼做负功，曲线逆时针变化。此为典型的摇滚运动状态。等幅振荡运动的幅值和频率受比例系数的影响，比例系数绝对值越大，其频率越快，振幅越小(见表3)。同时比例系数越大，曲线越接近一条直线。在一定范围内，比例控制器作用下后缘控制面的差动偏转能抑制三角翼摇滚的幅值。然而，受控稳定后三角翼摇滚振幅依然较大(φmax≥30)，且摇滚频率增加，三角翼所受到的最大气动力矩变大，对三角翼的结构强度提出更高的要求。因此，比例控制器不能对三角翼摇滚运动产生良好的控制效果。

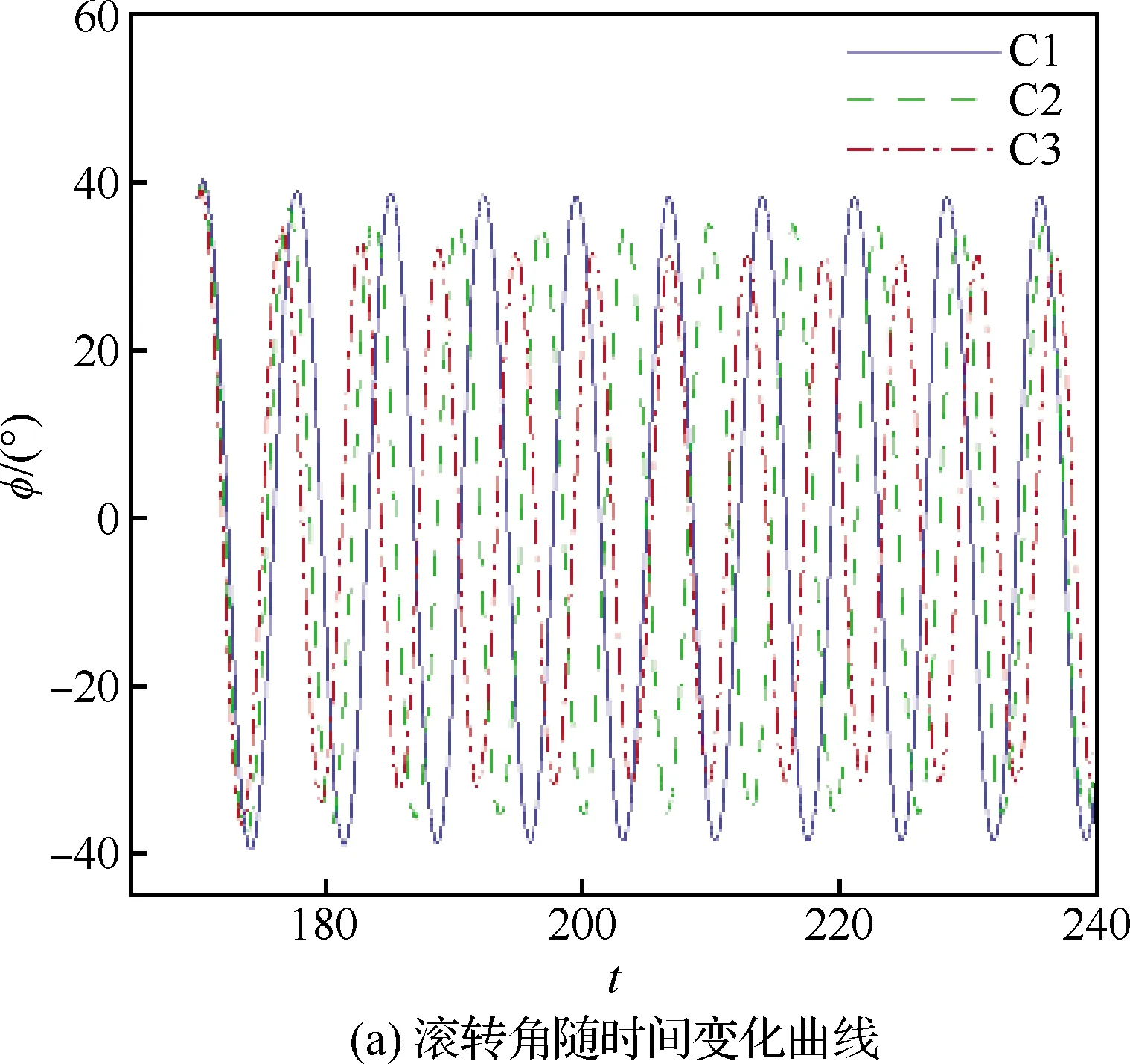
图5 不同比例控制系数的比例控制器作用下三角翼滚转运动数值模拟结果

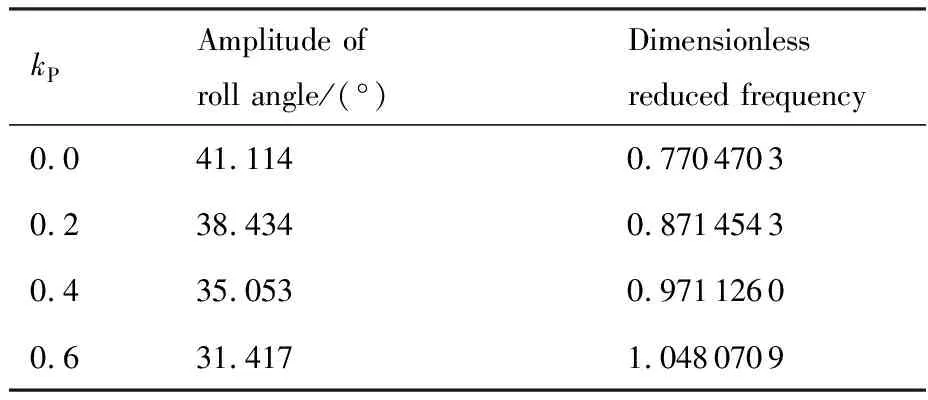
表3 不同比例系数下最终形成的极限环振幅和频率

在控制状态C3的基础上，增加微分项，数值模拟比例微分控制器(C4～C6)作用下三角翼的滚转运动，结果如图6所示。在施加控制后，三角翼滚转振幅逐渐减小，运动频率逐渐减缓，后缘控制面的偏转角随之减小。在计算时间内，C4控制状态下(kD=0.3)，三角翼滚转振幅被抑制在2°内。C5控制状态下(kD=0.2)，三角翼滚转振幅减小至10°以内，且有进一步减小的趋势，运动频率降低。C6控制状态下(kD=0.1)，三角翼进入振幅较小、频率较低的等幅振荡状态。图6(c)给出了数值模拟最后几个周期(t>220)，不同控制状态下三角翼滚转力矩随滚转角变化曲线。C6控制状态下，三角翼等幅振荡，曲线呈“双8”字，此为典型的摇滚运动状态；但与C3相比，曲线更为接近一条直线，气动加速、减速现象不明显。C4、C5控制状态下下，三角翼滚转力矩随滚转角逆时针变化，气流对三角翼做负功，三角翼滚转运动的振幅减小，且有进一步减小的趋势(图6(c))。在给定范围内，相比于比例控制器，比例微分控制器作用下后缘控制面的差动偏转对三角翼的摇滚的抑制作用更为明显，三角翼滚转振幅减小，滚转运动频率降低。

图6 不同微分控制系数的比例微分控制器作用下三角翼滚转运动数值模拟结果

5 控制面差动控制效果

结合三角翼流场和受力曲线进一步分析后缘控制面差动的控制效果。图7、图8给出了C3、C4控制器作用下，三角翼负行程(dφ/dt<0)3个 典型时刻，不同控制器作用下的流场图，并显示了背风面压力分布和流向不同位置(x=0.3,x=0.7,x=1.1)压力着色的截面流线。图9显示了控制作用下，三角翼控制面偏转角、滚转力矩随滚转角变化曲线(170.5≤t≤172.0)，并标明了3个典型时刻的位置。

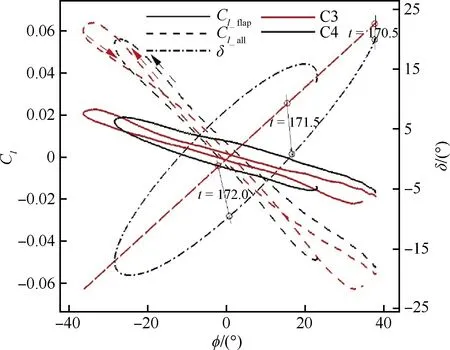
图9 不同控制器作用下控制面偏转角、滚转力矩随滚转角变化曲线

从流场图可以看出，控制面偏转对前缘涡非对称升降的影响十分小，不具备有效控制前缘涡的能力。控制面表面压力分布既受三角翼前缘涡的影响也受控制面偏转的影响。在三角翼滚转角较大时(如图7(a)、图8(a)所示)，比例、比例微分控制器作用下三角翼后缘控制面均有较大偏转。此时，上偏控制面形成压缩拐角，出现局部高压；下偏控制面虽然远离集中涡，但由于新的涡流的形成，出现了低压区。控制面差动运动使三角翼加速向零度滚转角滚转。比例控制器作用下，偏转角随着滚转角线性变化，当三角翼刚转过初始位置(φ=0°)时，控制面开始反向偏转，但角度很小，提供的反向控制力矩较小；同时，上偏一侧的翼面更为靠近前缘涡，进一步削弱了控制面提供反向控制力矩的能力(图7(c))。此时，总的滚转力矩随滚转角变化曲线存在顺时针的内环，三角翼在滚转角较小时处于加速偏转状态。而比例微分控制器作用下，微分项的存在使得控制面在转到初始位置之前，就开始反向偏转。当滚转较小时(图8(c))，三角翼上升一侧的控制面下偏，下降一侧控制面下偏，提供了一个与前缘涡升降趋势相反的控制力矩，使得总的滚转力矩随滚转角变化的零点向两侧移动，曲线顺时针内环消失，对三角翼滚转运动起到减速的效果。

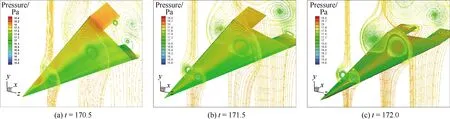
图7 比例控制器作用下三角翼典型时刻流场图

图8 比例微分控制器作用下三角翼典型时刻流场图

6 结 论

本文建立了气动、运动、控制多学科耦合数值模拟方法，基于线性模型选择控制器参数，模拟了三角翼摇滚运动的主动控制过程，分析了差动的后缘控制面在不同控制器作用下的控制效果。结果表明：采用比例、比例微分控制器，后缘控制面差动偏转均能使三角翼摇滚振幅减小。其中比例控制器作用下，三角翼摇滚振幅虽有一定的减小，但减小幅度不大，且摇滚频率有所增加。与比例控制器相比，比例微分控制器的控制效果更好：比例微分控制器作用下，控制面偏转既能抑制三角翼的滚转振幅又能降低三角翼的摇滚频率。选择合适的控制参数，三角翼的滚转振幅能被抑制在2°以内。结合流场分析，发现后缘控制面的差动偏转不具备有效控制三角翼前缘涡的能力。比例、比例微分控制器作用下，控制面偏转在三角翼滚转角较大时均会提供更强的减速滚转力矩；而在滚转角较小时，相比于比例控制器，比例微分控制器作用下的控制面能提供足够大的控制力矩使得三角翼滚转运动减速，破坏了“双8字” 的内环特性。这是比例微分控制器控制效果更好的原因。