燃烧多相流的介尺度动理学建模研究进展
许爱国,单奕铭, 陈锋,甘延标,林传栋
1.北京应用物理与计算数学研究所 计算物理实验室,北京 100088 2.北京理工大学 爆炸科学与技术国家重点实验室,北京 100081 3.北京大学 应用物理与技术研究中心 高能量密度物理数值模拟教育部重点实验室,北京 100871 4.山东交通学院 航空学院,济南 250357 5.北华航天工业学院 河北省跨气水介质飞行器重点实验室,廊坊 065000 6.中山大学 中法核工程与技术学院,珠海 519082
随着科技进步,人类飞行器的速度越来越高。“高速气流中的点火与持续燃烧成为空天推进中长久的关键问题”[1]。这些关键问题,往往涉及极端条件。极端条件,是相对于常温常压常速等普通条件而言的,它至少在某一方面严重偏离普通条件。随着科技发展,超声速、高瞬变已经成为航空领域司空见惯的条件和工况[2-3]。美国在20世纪 末提出了Hyper-X研究计划,通过研究一体化超燃冲压发动机技术从而实现马赫数7~15的飞行[4];俄罗斯也一直在进行高超声速飞行器的研究工作,比如“冷”计划(马赫数达到6.5,采用超燃冲压发动机)、“鹰”计划(马赫数达到12~14)、“针”计划(马赫数达到6~14,为空天飞机样机)。飞行器的高速运动导致流体与壁面间存在着极强的相互作用,大量动能转变为热能,高温使得理想气体模型失效,真实气体效应影响显著,同时也会对飞行器表面产生烧蚀作用,使其防热结构遭到破坏,从而改变飞行器气动性能,影响其稳定性和飞行安全性。并且在高温下飞行器表面的防热材料也会影响边界层内气体化学反应的催化效应,不同壁面催化条件会对气动热影响很大。
超声速、高瞬变等极端条件引发一系列值得深入研究的可压、非平衡复杂流动行为;非线性效应、离散效应、强耦合效应是其重要特征。这给传统流体建模理论的合理性带来严重挑战;同时,这些行为中的很大一部分又发生在微观分子动力学模拟无法企及的时间和空间尺度。例如,高空环境中的飞行器周围空气密度低,稀薄大气条件下连续介质假设失效,并且在不同的飞行高度上高超声速飞行器所处的环境状态也是不同的,由高空到低空分别处于自由分子流、过渡流、滑移流和连续流状态,这就需要对飞行进行跨尺度模拟。气体经过飞行器头部的强激波被极速加热,在气体稀薄效应和高温效应的共同作用下,气体分子的平动、转动、振动、电子能被同时激发,化学反应特征时间与流动特征时间几乎相当,飞行器的外流场表现出明显的非平衡性。而且,飞行器在飞行中,其周围的气体还存在层流到湍流的转捩现象,在湍流边界层的气动热更加严重。
基于求解Navier-Stokes方程组的传统计算流体力学(Computational Fluid Dynamics, CFD)已经在许多领域取得巨大的成功,但在航空、航天、微流控等领域也遇到了诸多新的瓶颈与挑战。其原因分为2个方面:① 物理建模层面的问题;② 离散格式带来的数值精度和稳定性问题。物理模型合理和具备相应功能是数值仿真研究的前提;物理建模层面的问题是无法通过数值精度的提高来解决的。鉴于一些燃烧相关的概念和技术(例如脉冲和旋转爆轰、微尺度燃烧、纳米推进剂、部分预混和层流燃烧、等离子体燃烧、冷火焰等)均涉及非平衡问题[5-19],也已有大量文献讨论离散格式等数值问题,同时鉴于作者团队的知识结构和研究经验主要在流体物理方面,本文从物理建模与复杂物理场分析角度,介绍离散玻尔兹曼建模方法(Discrete Boltzmann Modeling method, DBM)的研究进展[20-28]。本文结构如下:第1节回顾宏观与微观建模方法的特点;第2节介绍燃烧系统的DBM建模理论;第3节给出部分数值模拟结果;最后给出结论与说明。
1 宏观与微观建模
人们先前对燃烧和爆轰问题的研究主要依赖于实验及少量的理论分析[29-30],随着计算机技术的高速发展,燃烧和爆轰的数值模拟研究取得了巨大的成就[31-38]。数值模拟基于物理建模。燃烧系统的物理建模,有3个层次:微观、介观和宏观尺度。微观层次通常是指分子动力学(Molecular Dynamics, MD)描述[39-41],其中分子间作用势的确立是模型构建的关键,分子间作用势有效半径的选取是模拟过程中的关键,有效半径的选取通常以满足需求的最小值为最佳原则。微观研究可以帮助建立反应速率方程,提供完备信息,但由于运算量太大,对内存要求太高,因而适用的时空尺度非常有限。宏观尺度通常是指基于Euler或Navier-Stokes方程外加一个化学反应唯象模型的描述,其模拟手段以传统CFD方法为主[5,42-43]。近年来格子玻尔兹曼方法(Lattice Boltzmann Method, LBM)正在引起广泛兴趣[44-53],成为求解燃烧系统宏观流体力学方程组的另一手段。在宏观层次上人们关注的主要是系统的近平衡宏观行为,即密度、温度、流速、压强、应力、热流等物理量的演化,控制方程是代表质量、动量和能量守恒的流体力学方程组,本构关系往往是根据经验或唯象理论给出的。
2 介观动理学建模理论
从动理学理论和Chapman-Enskog多尺度分析角度看,如果系统时刻均处于局域热动平衡态,即在Chapman-Enskog多尺度分析时只保留Knudsen数(Kn)的零次方项,则Boltzmann方程对应的宏观流体方程组就是Euler方程组;如果系统时刻处于热动平衡态附近,二阶及以上非平衡效应很弱以至于可以忽略,只需考虑一阶非平衡效应,那么此时 Boltzmann方程对应的宏观流体方程组是Navier-Stokes方程组。也就是说,Euler方程实际上假设系统始终处于热力学平衡态,Navier-Stokes方程只包含了一阶的非平衡效应。而包括燃烧、爆轰在内的复杂流体系统内部往往存在大量的中间尺度的结构和动理学模式。结构小到一定程度会引发“离散效应”(相对于所关注的结构尺度,平均分子间距不再是可以忽略的小量,不能再使用连续性假设),模式快到一定程度会引发“热力学非平衡效应”(相对于所关注的模式的时间尺度,热力学弛豫时间不再是可以忽略的小量,不能再假设在模式演化的每一步系统都已回到热力学平衡态)。因而,系统内的这些小结构、快模式行为向Navier-Stokes方程等传统流体力学理论的物理合理性提出了挑战。同时,人们关注的行为特征往往又发生在微观分子动力学模拟无法企及的时空尺度上。这些“介尺度”的结构和行为因为模型和方法的缺乏(不成熟)而研究薄弱。这些薄弱不仅在一定程度上阻断了对微观到宏观之间关联的认识,也在一定程度上阻碍了本构模型的机理化、科学化;同时,微流控等技术的快速发展在提醒人们,这些(相对于宏观)特征更加丰富但以前知之甚少的“介尺度”非平衡、不连续行为,往往意味着大量待开发的物理功能。离散玻尔兹曼建模方法就是在这个背景下产生的理论模型构建方法。它是统计物理学相空间描述方法在离散玻尔兹曼方程形式下的进一步发展[54-59],其思想起源于许爱国等于2012年发表的一篇研究综述[54];在发展过程中又受到了形态相空间描述方法的启发[59-60]。DBM的研究思路是:将复杂问题进行分解,根据研究需求,选取一个视角,研究系统的一组动理学性质,因而要求描述这组性质的动理学矩在模型简化过程中保值;以该组动理学矩的独立分量为基,构建相空间,使用该相空间和其子空间来描述系统的状态和行为;研究视角和建模精度随着研究推进和实际需求而调整。一个DBM模型的建立,需要经历3个步骤。第1步,引入一个形式上的局域目标分布函数,将原来的碰撞项写成一个线性化碰撞算符的形式;要求是,所关心的物理特征量使用简化前和简化后的模型计算,所得的结果必须一致。第2步,借助离散速度,将原本连续、积分形式的动理学矩转化为求和进行计算;要求是,所关心的动理学矩转换为求和进行计算后,得到的结果必须相同,即
(1)
式中:ψ(v)=[1,v,vv,…]对应研究中关心的、建模过程中要保值的动理学矩,v为分子速度;fi=f(vi),vi为第i个离散速度。第3步,是DBM建模的目的和核心,给出非平衡状态和行为描述的具体方案。DBM建模主要针对的是宏观连续建模失效或物理功能不足、而微观分子动力学模拟又因为适用尺度问题无能为力的“介尺度”“两难”情形。DBM提供的物理信息量介于宏观连续描述和微观分子动力学之间。相对于宏观描述,DBM从一个更宽的视角来观测系统;DBM中非守恒矩描述的必要性和收益均随着非平衡程度的增高而增加。其与格子玻尔兹曼方法[44]、格子气方法[61]的关系如图1所示。早期的格子气方法,其本身就孕育了(至少)2个发展方向:① 统计物理学领域的粗粒化建模方法;② 计算数学领域的方程解法。1952年,李政道和杨振宁发表在《Physical Review》的《Statistical theory of equations of state and phase transitions.II.Lattice gas and Ising model》便是统计物理学领域构建和使用格子气粗粒化建模方法的实例之一[62]。通常认为,1988年开始出现LBM方法的雏形[61]。在1988—2012年期间,LBM方程解法和LBM建模方法在相互交织、相互启发中发展。LBM建模方法呈现出来的主要功能还是恢复宏观流体模型;与LBM方程解法相比,只是其在遵守物理规则方面要求更加严格,例如不允许使用非统计物理学意义下的“玻尔兹曼方程”、“矩关系”等,并未表现出与求解流体方程(组)功能的显著差异。于是,LBM基本上成了LBM方程解法的代名词。2012年,LBM方法与统计物理学非平衡行为基本描述方法相遇并碰撞出火花,LBM方法被注入统计物理学使用分布函数非守恒矩来描述非平衡状态和行为的思路,或者说统计物理学非平衡行为描述方法在离散玻尔兹曼方程形式下获得进一步发展[54]。随后,LBM建模方法与LBM方程解法的功能差异开始逐渐变得清晰。其中,起到关键促进作用的一步是相空间描述方法在离散玻尔兹曼方程形式下的进一步发展,这在后面还要提到。鉴于经常被误解为LBM方程解法,LBM建模方法逐渐改称为LB动理学建模(LB Kinetic Modeling, LBKM)、DBM。图1中DBM建模与分析方法轴上2012以后的点对应燃烧系统DBM建模文章发表的年份。需要指出的是,统计物理学领域作为粗粒化建模的格子气方法,不会因为DBM或其他建模方法的出现而消失,它的思路永远相对独立地存在和发展,在需要它的地方发挥作用。

图1 DBM、形态学描述方法和LBM的发展历程
模拟燃烧系统的DBM,其演化方程可统一写为[56]
(2)



(3)
式中:λ为化学反应进程参数;F(λ)表示反应速率函数。这样,便得到了Ci的表达式为
(4)

(5)
其中:ρ为密度;u为流速;Q为单位质量反应物完全反应后释放的热量,在本文中称之为爆热;e为内能密度。

(6)

(7)



图2 非平衡特征量张开的相空间
尽管爆轰研究已有100多年的历史, 但时至今日,它仍然是国际热点研究问题之一[11,13-14,16,66-69]。到目前为止,几乎所有获得广泛应用的化学反应模型均是唯象的或半唯象的。例如, Arrhenius反应率、森林火灾模型、两步模型、Cochran反应率模型、Lee-Tarver模型等。在实际应用过程中需要根据具体问题选择合适的化学反应模型。具体工况不同,点火的具体处理方式也就可能不同:化学反应的启动可能是由冲击引起的,也可能是烤燃、电击或摩擦等引起的,但其底层物理原因均是由于温度超过了化学反应的启动温度,反应物分子内的原子或原子团通过热运动挣脱它们之间的化学势引起的。在已发表的DBM文献中,使用的化学反应启动判据均是温度判据。同时需要说明的是,DBM既可以用于研究爆轰,也可以用于研究火焰。但一般意义下的火焰引发的热力学非平衡强度往往弱于爆轰,特别是强爆轰。非平衡效应越弱,则已有的传统流体建模就越能胜任;非平衡效应越强,则传统流体建模在物理功能方面就呈现出更多不足,DBM的必要性和优势也就越明显。
3 部分研究结果
近年来,DBM在燃烧(含爆轰)建模与模拟方面取得了一系列的进展,为非平衡燃烧(含爆轰)研究带来一系列新的物理认知和思考。

2014年,林传栋等[70]基于极坐标系构建了一个用于模拟燃烧的DBM,模拟了典型的内爆和外爆过程,观测并分析了化学反应热、物质输运、热传导与几何(汇聚或发散)效应的合作与竞争。在外爆过程中观测到了与一维爆轰情形不同的、几何效应导致的现象,例如熄爆、双向爆轰、稳定爆轰等。化学反应释放的热量使得系统局域温度升高, 而热传导和几何发散效应使得系统局域温度降低。所以,预先起爆区域的大小,影响着释放的热量是否足以克服几何发散效应引发的温度降低。如果之前的化学反应热足够多, 则化学反应得以维持;如果热传导和几何发散效应占优势, 则会出现熄爆现象。随着爆轰波向外传播, 几何发散效应逐渐减弱, 发生熄爆的可能性降低。发现在高度对称的系统中,球心处系统始终处于热力学平衡态。2018年,许爱国等提出一个单弛豫时间球坐标DBM模型[71]。在内爆与外爆过程中,几何汇聚与发散效应起到一个“外场力”的作用,更加细节的讨论参见文献[71]。

上述DBM均为单流体模型,即忽略介质成分差异,只关注其平均行为,产物和反应物所占份额用一个反应进程参数λ来描述。为了更加细致地描述反应系统,例如可以同时观测反应物和产物的不同流速和温度,2016年林传栋等[72]提出一个二流体燃烧DBM模型,在该模型中所有的反应物视为同一种介质(成分),所有的产物视为同一种介质(成分),反应物和产物分别使用2个不同的分布函数来描述,用2个相耦合的离散玻尔兹曼方程来描述反应物和产物的演化过程。该模型可用于模拟亚声速和超声速燃烧系统,比热比可调。相关宏观流体模型(例如带有化学反应的Navier-Stokes方程,Fick第一、第二定律,Stefan-Maxwell扩散方程等)均是该模型的特例,借助该模型可以很方便地观测和研究与宏观行为相伴随的各种热力学非平衡效应。为了更加细致地描述化学反应系统,体现反应物内不同介质(成分)、产物内不同介质(成分)之间的差异,进一步提出一个多流体DBM模型。作为应用实例,模拟研究了丙烷的氧化过程:C3H8+5O2→3CO2+4H2O。作为模型验证,除了密度、流速、温度、压强与理论解进行比对,定压燃烧的火焰温度(T)与实验结果符合较好[73],如图3所示。因为不同的反应物得以分别描述,所以该模型既可以描述预混燃烧,又可以描述非预混燃烧。
2.7 准确度考察(加样回收率试验) 取锥形瓶6个,分别精密加入新配制的大黄素-8-O-β-D-葡萄糖苷对照品溶液(66 μg∕mL)6.36 mL、大黄素甲醚-8-O-β-D-葡萄糖苷对照品溶液(48 μg∕mL)3.75 mL,减压回收溶剂至干,再精密称取已知含量供试品(6号供试品粉末,大黄素-8-O-β-D-葡萄糖苷含量为4.2 mg∕g,大黄素甲醚-8-O-β-D-葡萄糖含量为1.8 mg∕g),各称取约0.10 g,分别精密称定,按“2.3”项下制备供试品溶液。进样测定,按下式计算回收率。
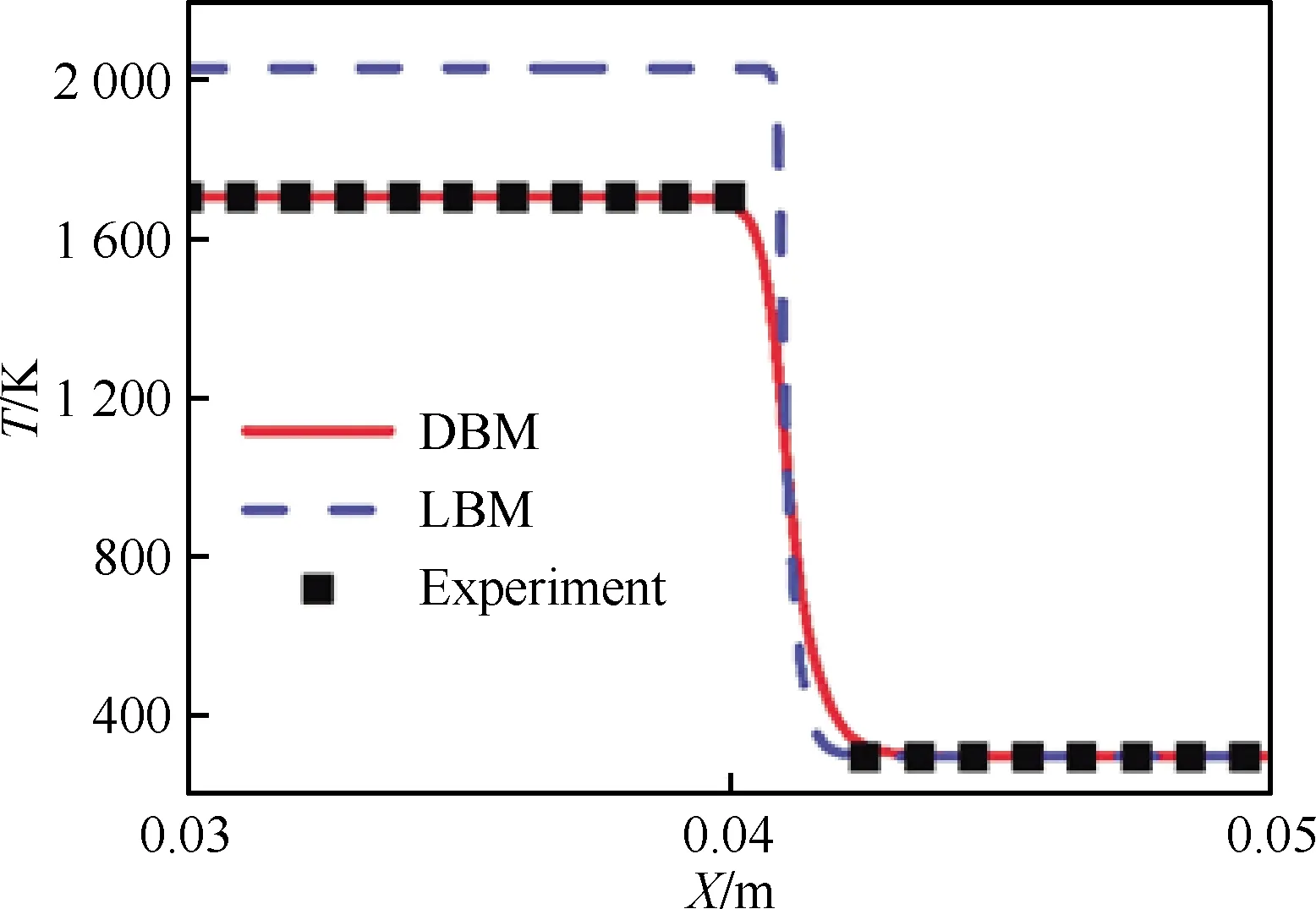
图3 定压燃烧火焰温度分布[73]
关于含外场力情形的燃烧DBM建模可参考文献[74]。如果令式(2)中的Force Term=-Fi,则在分布函数偏离平衡部分(f-feq)对外场力效应影响较小,且化学反应的时间尺度远大于热力学弛豫时间的情形,在BGK(Bhatanger-Gross-Krook)模型框架下外场力和化学反应引发的分布函数变化率可写为
(8)
式(8)的含义为:在时间间隔τ内,流速由u变化为u+aτ,温度由T变为T+τT′。由外力和化学反应而引起的能量的变化率为
E′=ρu·a+ρQλ′
(9)
根据E=(D+I)ρT/2+ρu·u/2和式(9),可以得到温度的变化率为
(10)
式中:D代表维度;I代表与分子旋转和/或内部振动相对应的额外自由度。反应进度参数λ定义为反应产物与混合物的质量比。在文献[74]中,作为实例,化学反应进程由Cochran速率函数控制:
λ′=ω1pm(1-λ)+ω2pnλ(1-λ)
(11)
由式(11)可知,λ′依赖于压强p=ρT,而ω1、ω2、m和n均为可调参数。


图4 爆轰波附近的各物理量[75]
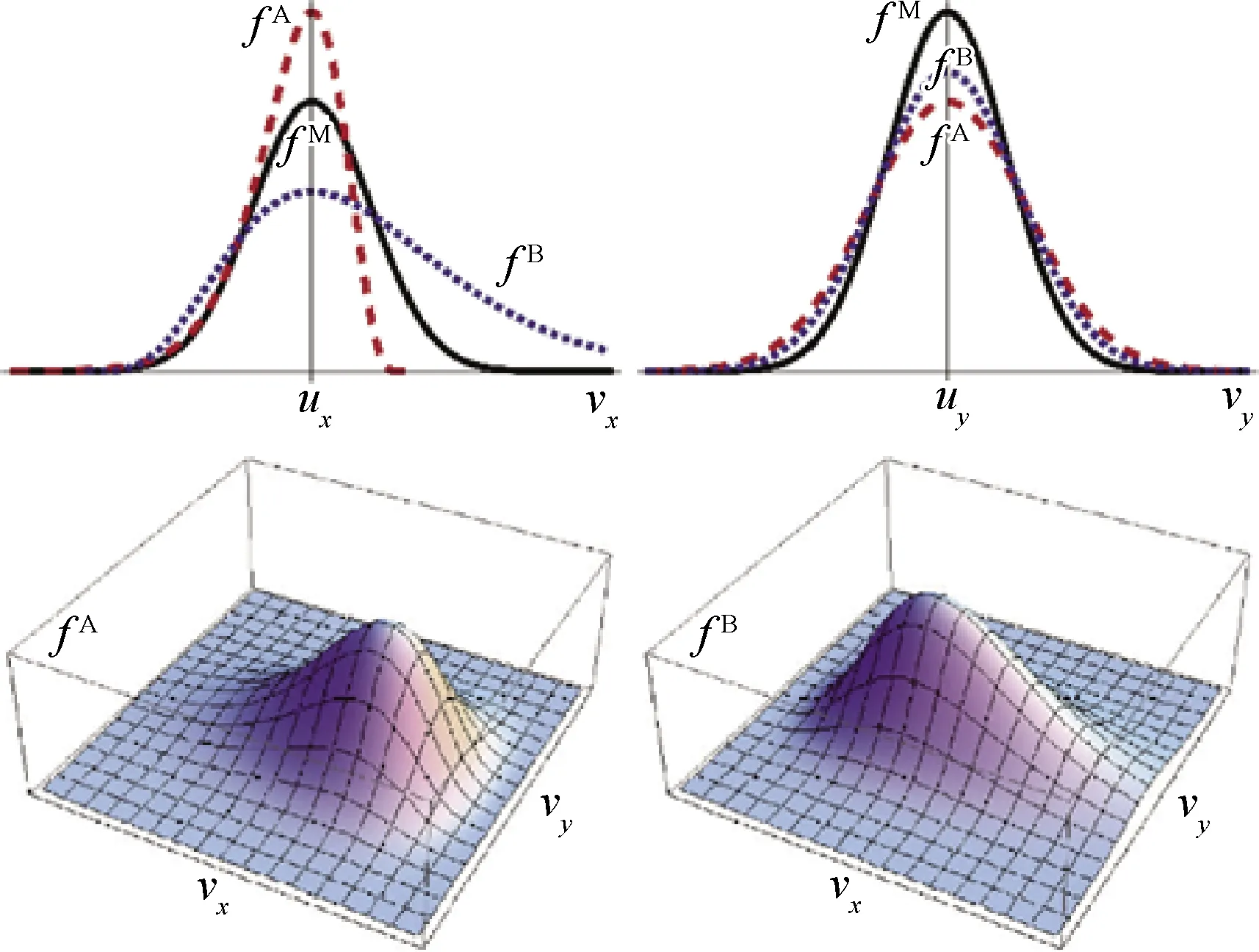
图5 反应物和产物在压强峰值处的速度分布函数主要特征[75]


图6 非平衡效应与化学反应放热的关系[75]
为了估算爆轰波波峰的相对高度,定义了峰高H(q)=(qmax-qs)/(qvon-qs),其中q指代各宏观物理量,qmax为在爆轰波附近q的最大值,qs为CJ解而qvon是在冯·纽曼峰处的ZND解。除此之外,通过比较可以发现:① 考虑非平衡效应的爆轰波波峰要低于不考虑非平衡效应的结果;② 考虑非平衡效应的爆轰波波阵面比不考虑非平衡效应情形要宽;③ 考虑非平衡效应的物理量的梯度要比不考虑非平衡效应情形的小。
2016年,张玉东等[23]利用DBM研究了带有爆轰的反应流问题,从理论上推导了一套新的流体力学方程,方程中的应力和热流用文中定义的2个非平衡量(无组织动量流和无组织能量流)进行代替。基于所提出的动理学模型,将2个非平衡量和熵产生速率之间建立起关系,并研究了负温度系数对爆轰演化过程的影响。使用的化学反应率模型为
(12)
其中:

(13)
(14)
(15)
式中:Tth为起爆温度;k为化学反应速率系数;h1和h2分别代表了k的峰值和谷值;T1和T2分别是h1和h2对应的温度。研究了图7(a)~图7(d)所示4种反应速率系数下的爆轰现象。通过比较可以发现,对于4种反应速率特性的爆轰情形,在远离爆轰波阵面附近以及化学反应区,无组织动量流与应力、无组织能量流与热流均有一些差异,而这些区域也正是非平衡特征最显著的地方。当地的熵产生有3个来源:化学反应、无组织动量流以及无组织能量流。对于系统内的全局熵产生,化学反应所占的比例远大于另外2个方面,无组织动量流导致的熵产生率大于无组织能量流产生的熵产生率。负温度系数对动力学量的作用是降低冯·纽曼峰的高度(减小密度、压强和速度),加宽反应区,抑制化学反应进程。

图7 5种反应速率系数随温度变化特征图[23]
2019年,张玉东等[76]提出了一个用于模拟爆轰的一维离散玻尔兹曼模型。通过对Sod激波管问题、Colella爆炸波问题和一维自持稳定爆轰传播问题进行模拟,并与相应的解析解进行比较,数值验证了该模型的有效性。在该工作中研究了由于负温度系数而导致的一种反常爆轰现象,此时的化学反应速率系数k的表达式为
k(T)=a+b[T3/3-(T1+T2)T2/2+T1T2T]
(16)
式中:系数a和b由式(14)和式(15)给出。在本工作中,h1=2 000,h2=10,T1=1.14,T2=1.45,起爆温度Tth=1.1。化学反应速率系数与温度之间的关系如图7(e)所示,从图中可以清楚地看到,存在一个负温度系数区间(Ti,Tj),反应速率系数随着温度的升高而减小。
图8[76]为恒定的化学反应速率系数与负温度系数2种情形下的爆轰波模拟结果。2个结果之间除了化学反应速率和网格数之外其他参数均一致,从图中可以明显发现在负温度系数条件下出现了反常的爆轰现象。对于反常爆轰来说,其并没有一个恒定的波速,并且波形是随时间周期性变化的。
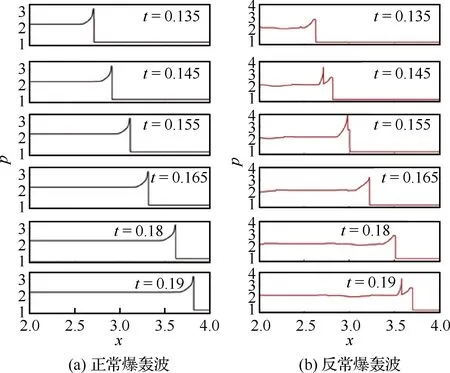
图8 正常爆轰波与反常爆轰波的比较[76]
为了方便讨论,根据温度将化学反应大致分为3个阶段,如图7(e)所示,这3个阶段分别记为S1、S2和S3,其中第1阶段S1处于低温区域,但由于负温度系数的缘故导致其具有较快的反应速率,第2阶段S2在特定温度范围内具有较慢的反应速率,而第3阶段S3在较高温度下具有较快的反应速率并且反应速率随着温度的升高而显著的增加。通过研究发现,对于常规的爆轰现象,化学反应主要发生在S1和S2阶段中,但对于该反常爆轰,在S3阶段中的某个时间会产生一个局部热点,然后在旧的爆轰波波阵面后方出现具有更剧烈化学反应的新爆轰波,这个新爆轰波拥有比前面爆轰波更快的波速,它紧追前波,最后2个爆轰波合并,之后爆轰波的波速开始减慢直到它达到CJ爆轰值。在此之后局部热点再次出现并重复上述过程,如图9[76]所示。

图9 反常爆轰现象的发展过程示意图[76]
上面DBM模型使用的均是单步反应模型。2020年,林传栋和罗开红[77]利用含化学反应的DBM研究了考虑非平衡效应的非稳定爆轰现象,该研究中使用了以下两步链式化学反应模型[78]:
(17)
λ′=(1-W)kR(1-λ)exp(-ERT-1)
(18)
式中:ξ′和λ′分别为点火阶段以及化学反应放热阶段中的反应进程参数随时间的导数;Ts为初始
冲击温度;EI为描述化学诱导过程中温度敏感性的全局活化能;kI为点火过程方程中指数前的参数;W=W(ξ)为阶梯函数,当ξ<1时,W=1,当ξ≥1时,W=0;ER为活化能;kR为放热过程方程中指数前的参数。在该工作中分别研究了扰动振幅、波长以及化学反应放热对非稳态爆轰的影响,发现初始扰动幅度仅影响初始阶段非稳定自持爆轰的形成,当初始扰动具有较小的波长时,压强在早期阶段以更高的振荡频率更快地增加,但之后很快减小,并在后期阶段变得更小,此时全局非平衡强度更大,但如果波长足够小则全局非平衡强度较小,在这种情况下,最大压强则展示出相对小振幅、小平均值以及一个长的振荡周期。此外,还发现随着化学反应放热的增加,压强和它的振幅增大,非平衡效应也增强,但振荡周期减小。如果扰动的波长足够小,则不存在横波或胞格结构,并且二维非定常爆轰会减弱为一维爆轰。
关于冲击波附近的流体动力学和热力学非平衡效应,林传栋等[79]通过定义绝对和相对偏差度来描述流体系统偏离平衡态的程度,研究了冲击波局部和整体的非平衡效应以及非组织能量流及其通量,并对驰豫时间、马赫数、热导率、黏性和比热比对冲击波处非平衡效应的影响进行了研究。2021年,吉雨等[80]提出了一个含化学反应的三维多驰豫DBM,该模型可以自由调节普朗特数和比热比。通过引入Arrhenius不可逆、单步化学反应模型,模拟自由下落过程中的化学反应、Couette流、一维稳态和非稳态爆轰以及在封闭立方体中的三维球形爆炸验证了新模型的正确性。图10给出该模型的一组模拟结果:外爆过程中3个时刻的压强场分布。

图10 外爆过程中压强场的演化过程[80]
4 结论与说明
超声速、高瞬变等极端条件引发一系列值得深入研究的可压、非平衡复杂流动行为;非线性效应、离散效应、强耦合效应是其重要特征。随着流体行为非平衡程度增强,只关注分布函数守恒矩(密度、动量和能量)演化的描述方法在物理功能方面越来越不能满足需求。其表现之一是:不考虑非平衡效应或者非平衡效应处理不当,直接影响着密度、流速、温度、压强这些常用宏观量结果的精度。另外,这些以前因模型、方法原因而知之甚少的非平衡行为特征蕴含着大量待开发的物理功能。发展DBM等介尺度建模和模拟方法,研究这些非平衡行为特征;基于获得的新认识,开发新的物理功能正在成为该研究方向的重要内容。
需要说明的是:① DBM建模方法主要是针对宏观连续建模失效或物理功能不足、而微观分子动力学模拟又因为适用尺度问题无能为力的“介尺度”情形,应“介尺度”非平衡系统研究需求而设计的物理模型构建方法;② DBM提供的物理信息量介于宏观连续描述和微观分子动力学之间;③ 相对于宏观描述,DBM从一个更宽的视角来观测系统;④ DBM中非守恒矩描述的必要性和收益均随着非平衡程度增高而增加;⑤ 与不含化学反应的复杂流动相比,燃烧系统的热力学非平衡多了一个来源:快速反应。当化学反应速率加快到一定程度,便不能再假设在化学反应进程的每一步系统都回到了热力学平衡态;⑥ 目前已公开发表的DBM研究涉及的只是相对稀薄和快速流动引发的热力学非平衡。同时,尽管DBM可以在非平衡行为描述的广度与深度2个方面超越Navier-Stokes方程,但鉴于研究的阶段性,目前已公开发表的燃烧系统的DBM研究主要集中在DBM的描述广度方面;且其应用研究也远不如在相分离[28,81-84]和流体不稳定性研究[21-22,24,26,64,85-90]方面充分,除此之外,目前的DBM燃烧多相模拟中的多相主要指燃烧过程中的多组分流体。因而,包含化学反应非平衡的DBM建模与模拟、在非平衡深度描述方面超越Navier-Stokes方程的DBM建模、分布函数f对平衡态feq的偏离(f-feq)对外力项效应影响较大情形的DBM建模与模拟、多个相(态)的DBM燃烧模拟、燃烧多相流系统的深度非平衡动理学机理与应用均是下一步研究工作的重点。
致 谢
感谢闫铂、张玉东、赖惠林、罗开红、陈正、王健平、王兵、聂百胜、王成、孙远翔等在燃烧建模与模拟方面和王立锋、赵英奎等在内爆动理学等方面的有益讨论。

