双层旋转锥形液膜一次破碎特性数值研究

申力鑫，邢菲，秦腊，苏昊

厦门大学 航空航天学院，厦门 361000

离心式喷嘴是一种机械压力式雾化喷嘴，广泛应用于燃气轮机、航空发动机、内燃机、工业炉、农业喷雾、喷漆等领域。根据其结构的差别，可以分为切向孔离心式喷嘴[1]、锥形涡流器离心式喷嘴[2]和溢出回流式离心式喷嘴[3]等。其中，由于切向孔离心式喷嘴结构简单，能保证在复杂恶劣情况下的可靠性和稳定性，在航空领域的发动机[4-5]中得到了广泛应用。液体通过切向孔进入旋流室，由于剧烈的离心运动在喷嘴出口处生成一个旋转的锥形液膜，锥形液膜在湍流、气动力、表面张力等因素的作用下经过一次破碎和二次雾化最终形成小液滴群。

离心式喷嘴在喷嘴出口处形成的液膜为旋转锥形液膜，液膜破碎产生大小形状各不相同的、离散的液块、液丝和大液滴的过程称为一次破碎，其过程涉及气动稳定性、空化、湍流等多种因素，极为复杂。二次雾化指在一次破碎的基础上，在气动力和表面张力的共同作用下，液丝、液块和大液滴破碎形成小液滴群的过程，因此在某种程度上一次破碎决定了喷嘴二次雾化的雾化特性，基于此，对旋转锥形液膜一次破碎的研究就显得极为重要。而在喷嘴出口处添加同轴旋转的环缝空气则可以与液相相互作用，增强雾化和掺混，从而改善高雾化和燃烧性能。在此过程中有一个重要的参数——气液比(Gas Liquid Ratio, GLR)，不同的GLR对锥形液膜的破碎与雾化有着重要的影响，当前国内外学者已经对其进行了大量的研究[6-8]。

在锥形液膜的理论研究方面，岳明和杨茂林[9]在考虑喷雾锥角和液膜向下游发展逐渐变薄的条件下推导了色散方程，Fu等[10]推导的色散方程形式与岳明和杨茂林[9]的相同，且其研究表明正弦模式扰动波增长率大于曲张模式，实际喷雾中正弦模式所占权重越大，液膜破碎时间越短。Hosseinalipour等[11]在考虑喷雾锥角的条件下推导了同轴气体作用下锥形液膜的色散方程，其研究表明液体旋转、气液密度比会促进液膜的不稳定，增大喷雾锥角和液膜厚度能够显著提高表面波增长率。

在锥形液膜的数值仿真和试验研究方面，Reddy和Banerjee[12]采用数值模拟的方法对锥形液膜的一次破碎进行了研究，结果表明液膜厚度的增加会导致液膜破碎长度的增加。王凯等[13]采用数值模拟和试验的方法对离心式喷嘴锥形液膜破碎过程进行了研究，结果表明切向孔直径对液膜锥角和液滴平均粒径的影响较显著。刘娟[7]采用试验方法观测了旋转锥形液膜的一次破碎过程，通过对图像的处理得到了液膜破碎长度和液膜破碎时表面波长，总结了适用于离心式喷嘴使用的破碎长度公式，公式中的破碎长度系数与喷嘴几何特性参数关系较大。康忠涛[14]采用试验和理论相结合的方法研究了环缝气体对气液同轴离心式喷嘴液膜表面波发展的影响，发现其主要与气液相对运动速度有关，气液相对运动速度会影响液膜的主导表面波模式、表面波增长率、液膜破碎时间和破碎长度，同时，反压会促进表面波发展，而喷嘴等直段会抑制表面波发展。

当前的研究大多针对单路离心式喷嘴产生的单层旋转锥形液膜，而在实际的航空发动机中，双路离心式喷嘴因其流量调节范围大，适用于多种工况和飞行条件，应用范围要比单路离心式喷嘴更为广泛。而目前对双路离心式喷嘴产生的双层旋转锥形液膜[15-16]的研究比较少。本文以双路离心式喷嘴为研究对象，通过改变喷嘴进出口压降和同轴旋转空气轴向速度设置9个工况，采用流体体积(Volume of Fluid, VOF)方法和八叉树自适应网格加密(Adaptive Mesh Refinement, AMR)技术对双层旋转锥形液膜的一次破碎进行数值模拟，研究不同压降、双层液膜相互作用和同轴旋转气流速度对液膜一次破碎的影响。

1 数学物理模型

1.1 数值方法

双层旋转锥形液膜的一次破碎采用开源计算程序包Gerris进行数值模拟，其详细数值方法见文献[17-18]，求解的是三维、不可压缩、带有表面张力的Navier-Stokes方程：

(1)

(2)

式中：u=(x,y,z)为流体速度；ρ=ρ(x,t)为流体密度；p为压力；μ=μ(x,t)为动力黏度；D为变形张量，定义为Dij=(∂iuj+∂jui)/2；δs为狄拉克分布函数，表示表面张力集中在气液两相的交界面上；σ为表面张力系数；κ和n分别为气液交界面的曲率和法向量。

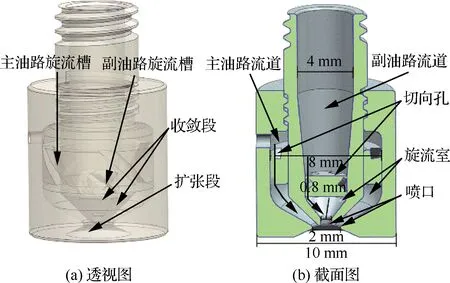
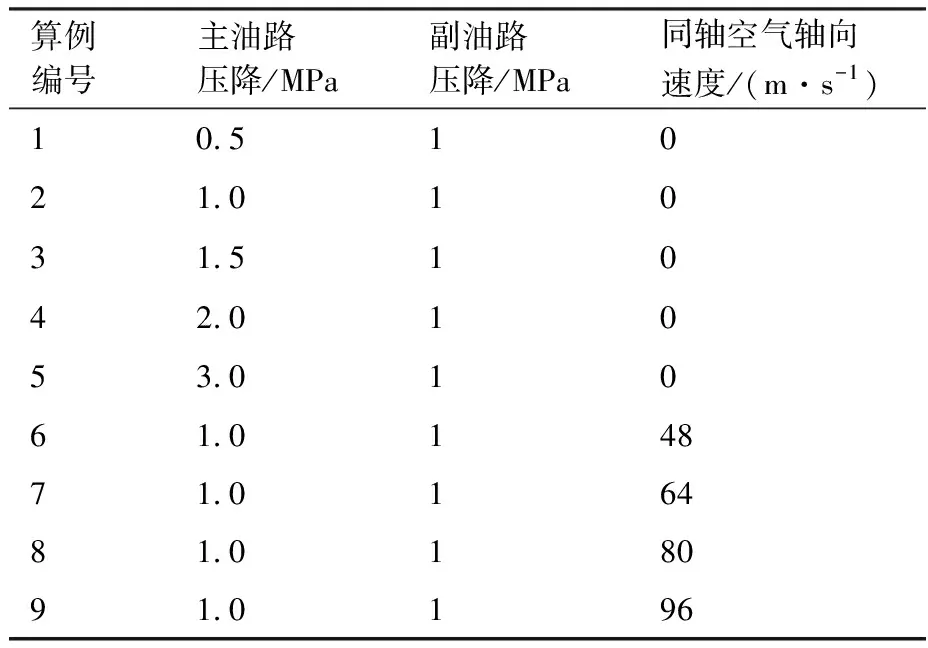
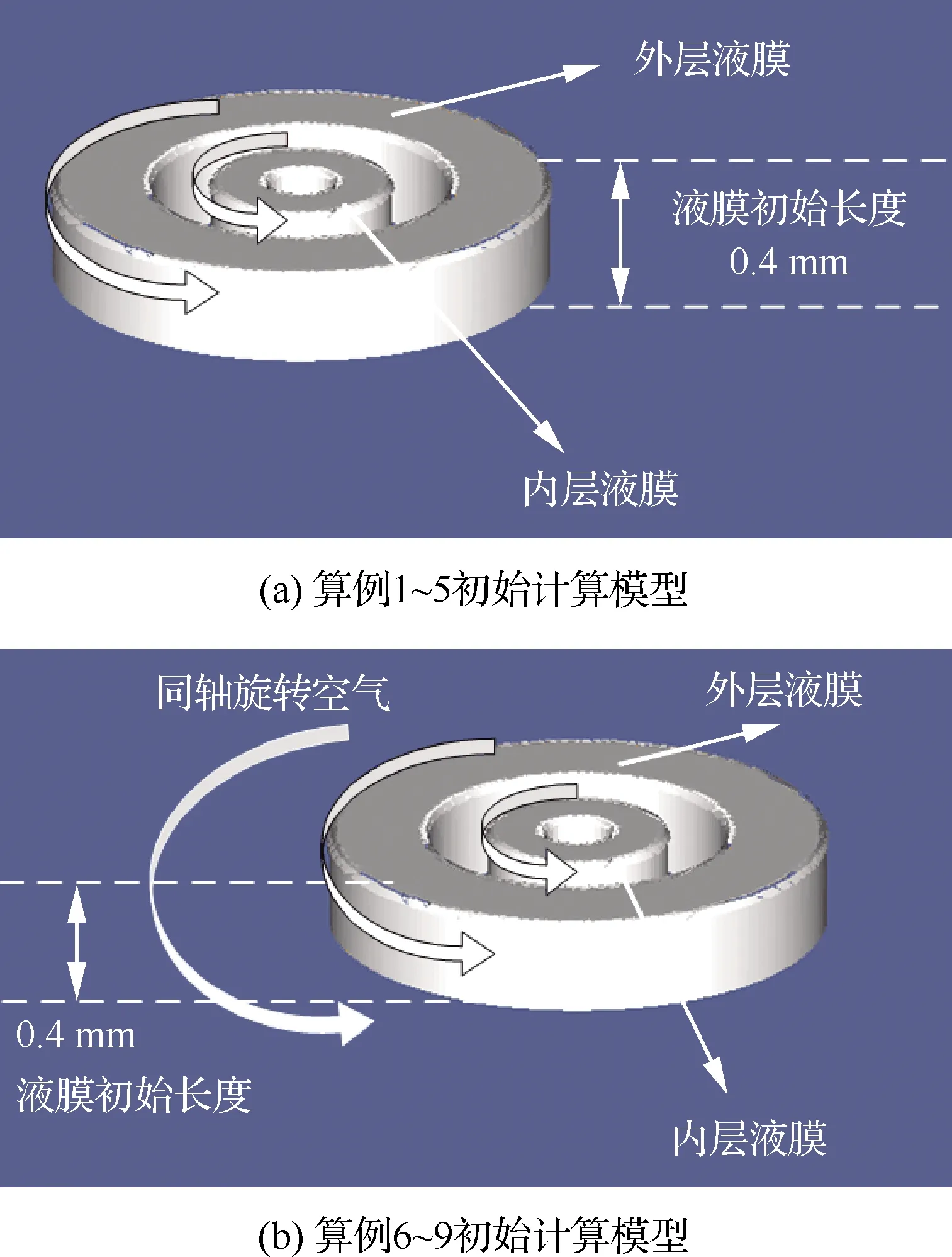
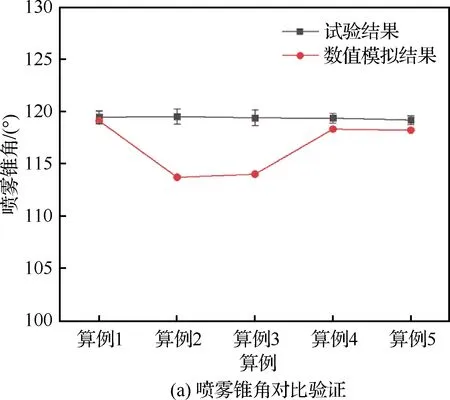
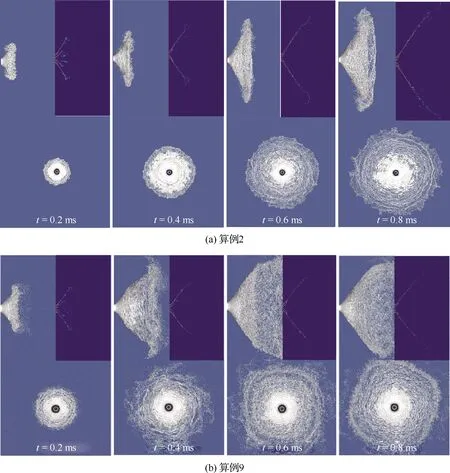
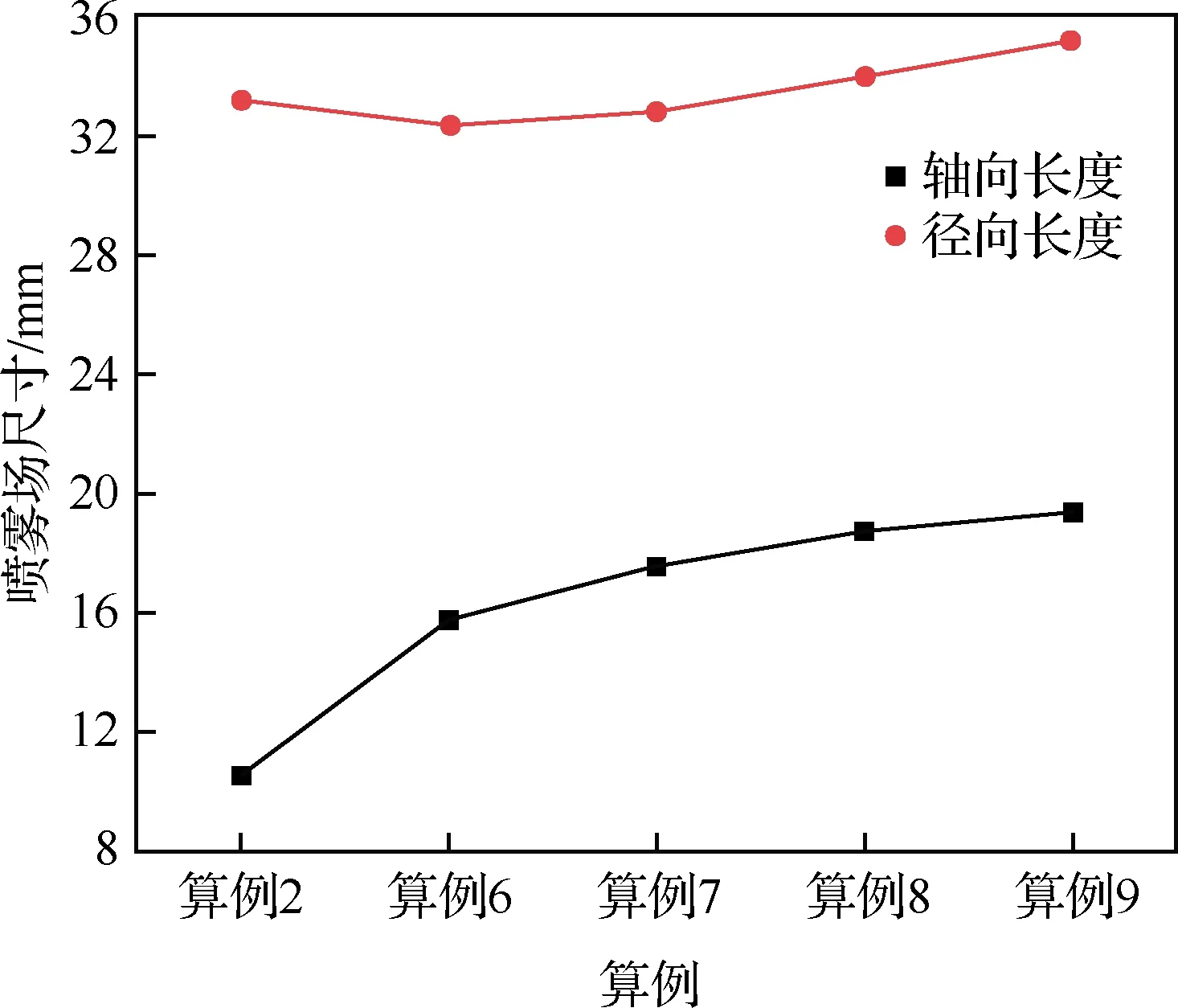
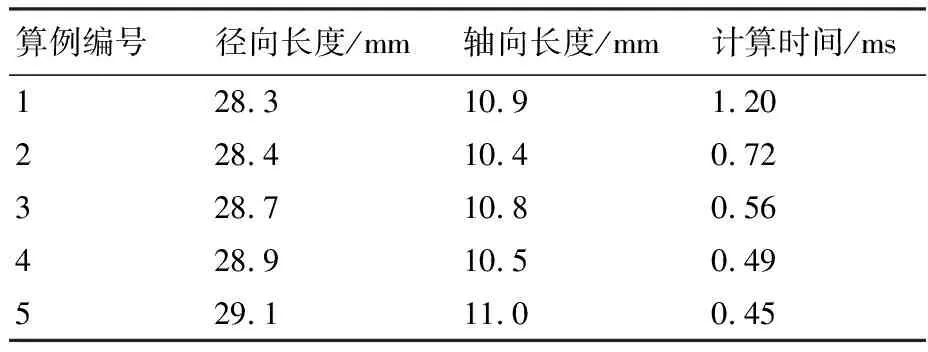
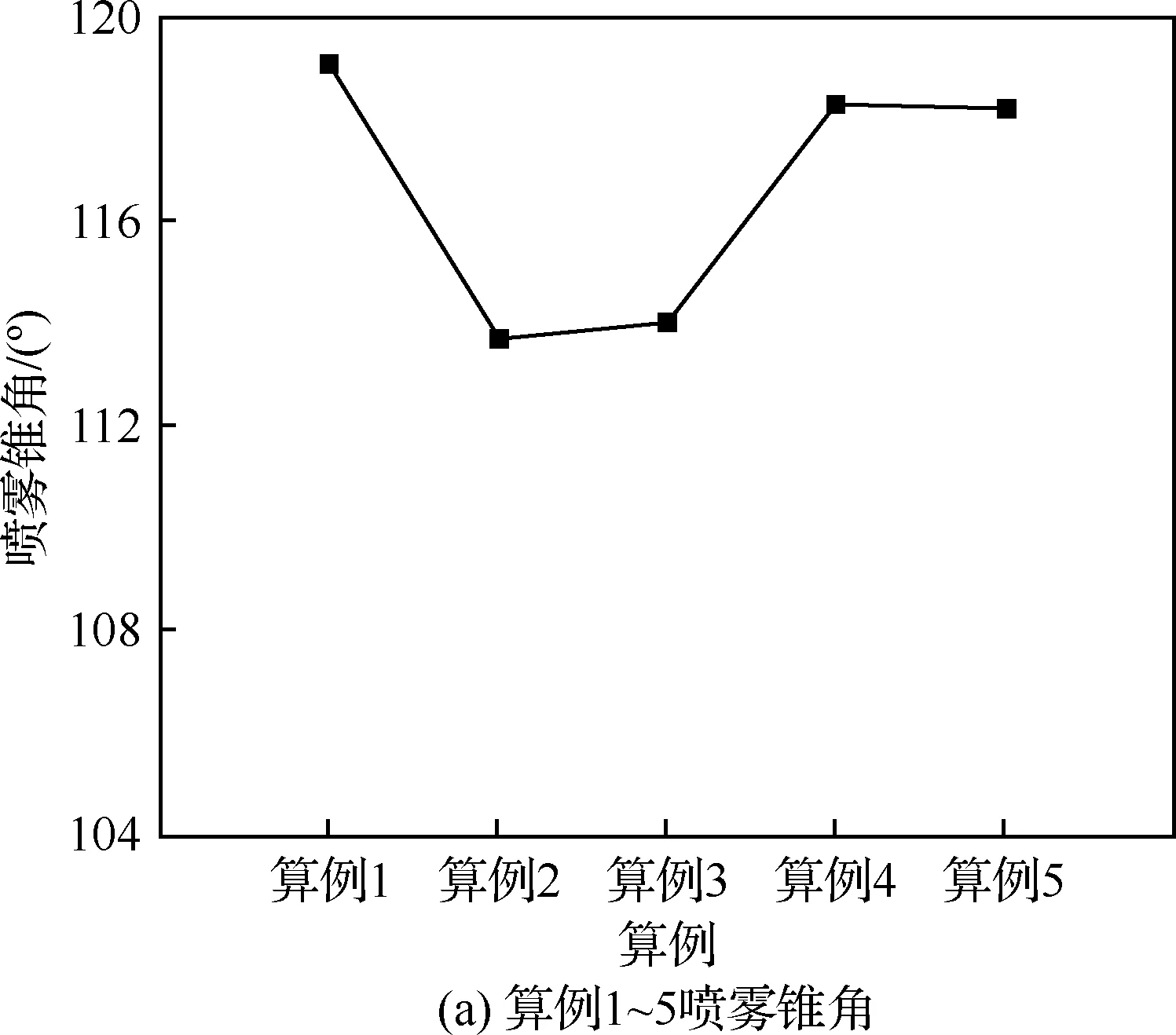
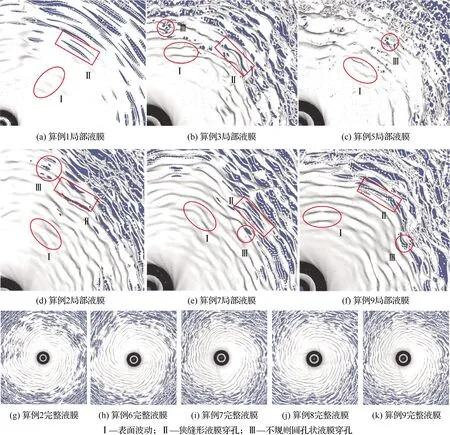
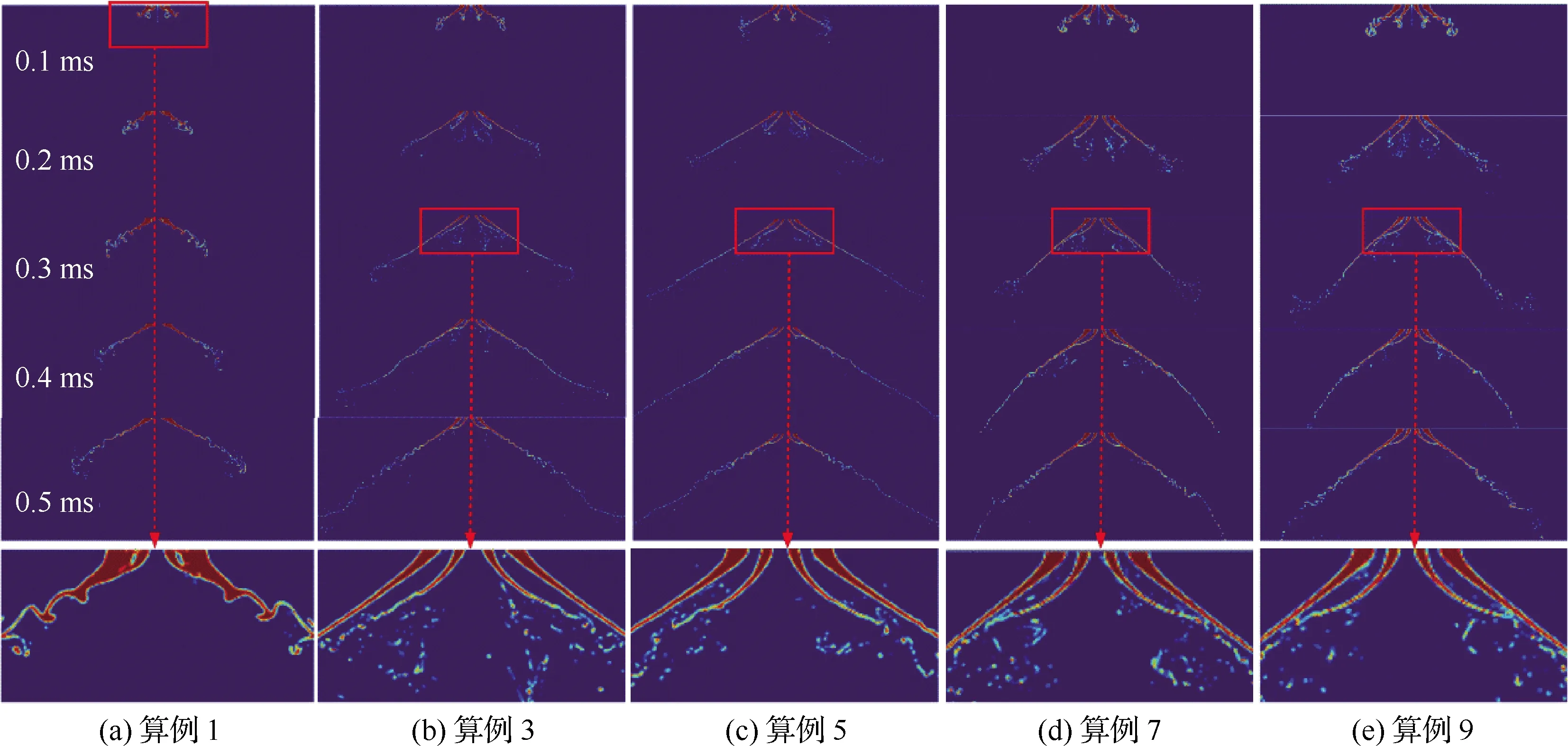
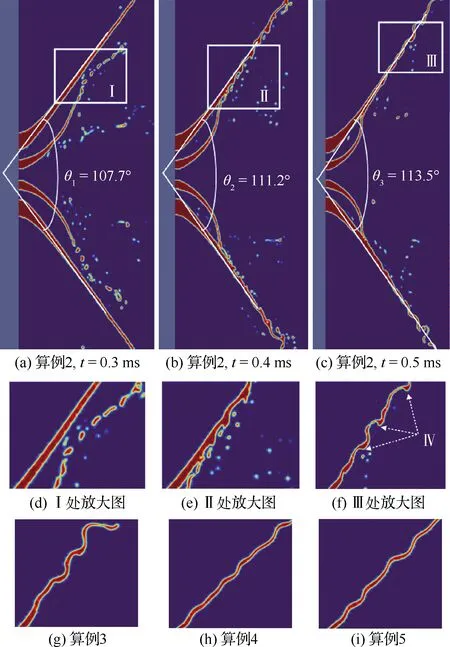
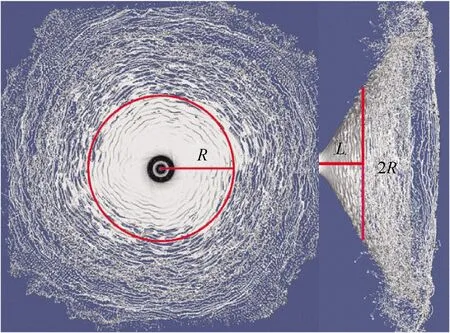
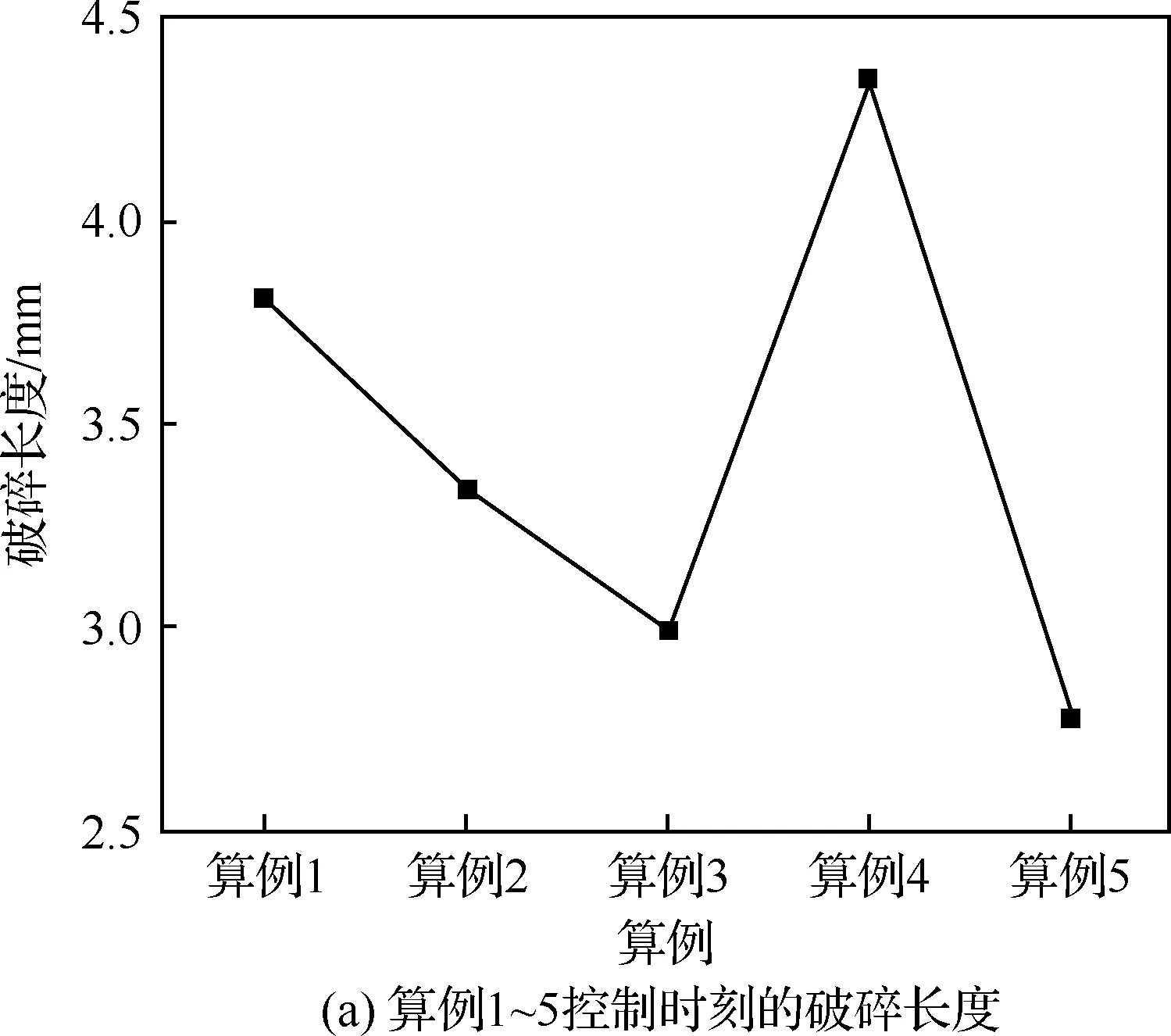
对于气液两相流动，使用VOF方法将流体体积分数T引入每个计算单元，当计算单元中充满液体时T=1，充满气体时T=0，当计算单元为气液相界面时0

ρ(T)=ρlT+ρg(1-T)

(3)

μ(T)=μlT+μg(1-T)

(4)

式中：ρl和μl分别为液体的密度和黏度；ρg和μg分别为气体的密度和黏度。对体积分数T、密度和压力使用时间交错离散方法可以得出二阶精度时间离散方程，然后使用经典的时间分裂投影法(Time-Splitting Projection Method)[19]进一步简化。计算域的空间离散使用八叉树结构进行离散，达到了空间二阶精度。表面张力的估算采用压力校正方法，使压力梯度与表面张力达到精确的平衡，湍流的处理采用单调集成大涡模拟方法(Monotone Integrated Large Eddy Simulation, MILES)，又称隐式大涡模拟(Implicit Large Eddy Simulation, ILES)[20]。

采用分段线性界面重构(Piecewise Linear Interface Construction, PLIC)方法进行界面重构，采用基于八叉树的AMR技术和并行技术来加快计算速度，根据流体体积分数值和梯度对网格进行加密。仿真域由50个L×L×L的基本结构BOX组成，其中L=4 mm。Chen等[21]的网格加密和验证研究表明，9级网格足以满足气液界面的加密要求，5级网格足以满足气相的加密要求。本文采用相同的设置，且9级网格对应的最小网格尺寸为7.8 μm，足以满足对于雾化问题的高精度模拟和小液滴的捕捉。图1为雾化数值模拟过程中的自适应网格加密。

图1 雾化数值模拟过程中的自适应网格加密

1.2 计算模型

计算用的喷嘴模型如图2所示，红色箭头表示主油路和副油路的流动路径。高压液体分别从主、副流道进入喷嘴，经过切向孔逆时针旋转后进入旋流室，在离心力的作用下形成中心气核，以锥形液膜的形式从喷嘴出口喷出。喷嘴的主要结构参数如下：总长度16.5 mm，主、副流道直径分别为8.0、4.0 mm，主、副流道切向孔数目均为4，主、副油路喷口直径分别为2.0、0.8 mm。

图2 喷嘴几何模型

设置算例1～5共5个不同的主副油路压降，使用商业计算软件Fluent计算喷嘴的内部流动，使用压力入口边界和压力出口边界，壁面均为无滑移壁面边界，空气为第1相，水为第2相。使用VOF方法计算喷嘴内部两相流动，压力离散方法为PRESTO，压力速度耦合方法采用COUPLE，动量方程等均采用二阶迎风格式，湍流模型选用带旋流修正的Realizablek-ε模型。计算得到喷嘴出口截面处液膜厚度、液膜轴向速度、切向速度和径向速度等信息，然后将其作为初始条件导入开源计算程序Gerris中进行外喷雾场的数值模拟。在保证数据准确传递的基础上，将Fluent采用贴体网格计算内流场的优势与Gerris采用AMR技术、PLIC方法计算外喷雾场的优势相结合，解决单独使用 Gerris计算喷嘴全流场时，用笛卡尔网格逼近轴对称固壁时存在的网格非体贴效应问题，从而实现离心式喷嘴从内而外的一体化准确计算[13]。同时在算例2的基础上，加入同轴旋转空气参与外流场的雾化，旋转方向与锥形液膜旋转方向相同，旋转空气的夹角定义与喷雾角定义相同，数值为85.5°。设置算例6～9共4个不同空气轴向速度的算例进行数值模拟。9个算例的初始计算模型如图3所示，箭头所示的分别为内外液膜及空气旋转方向，主要模拟工况和参数如表1所示。

表1 各算例主要模拟工况与参数

图3 各算例初始计算模型

1.3 算例验证

对算例1～5分别进行数值模拟和试验，对算例6～9只进行数值模拟。试验中，采用图2所示喷嘴，在算例1～5对应的压降下进行雾化试验，使用高速摄像机拍摄喷嘴雾化过程，使用相位多普勒干涉仪(Phase Diameter Interferometer，PDI)测量喷雾场液滴尺寸。图4比较了试验和数值模拟的喷雾场宏观形态，图4(a)、图4(b)分别为算例2喷雾场的数值模拟结果和高速摄像机拍摄结果，两者比较来看，都有相同的喷雾特征，包括液膜破碎长度(I)、液膜表面波动(II)、液膜穿孔(III)、液丝(IV)、液滴(V)。图4(c)为算例9的喷雾场数值模拟结果，图4(d)则是文献[15]中气液比较大时气液同轴双离心喷嘴雾化图，对比来看，两者有相似的工作条件和宏观轮廓。

[5][50] Hodler. R., Raschky. P, “Regional Favoritism”, Quarterly Journal of Economics, Vol. 129, No. 2 (2014), pp. 95-103.

图4 喷雾场宏观形态的对比验证

在进行雾化试验时，由于分辨率、飞溅液滴、背景干扰等因素的影响，导致用高速摄像机拍摄得到的喷雾场图像液膜边界不够清晰，难以获得较为准确的喷雾锥角，为此采用MATLAB对图像统一进行如图5(a)～图5(d)所示的方法处理。针对算例1～5的试验结果，随机取10张高速摄像拍摄得到的图像进行处理得到喷雾锥角，然后求喷雾锥角平均值和标准偏差。而针对算例1～5数值计算结果，直接采用线拟合的方法得到喷雾锥角。

图5 试验图片喷雾锥角获取方法

对于索特尔平均直径(Sauter Mean Diameter，SMD)的验证，针对算例1～5，在试验数据方面，取距喷嘴出口轴向距离10 mm截面处的5个位置，采用PDI进行测量，对得到的5个数据进行处理，得到平均值和标准偏差。在数值计算数据方面，对喷雾场轴向位置9.5～10.5 mm处所有液滴的体积数据进行统计并计算各个液滴的直径，去除直径大于200 μm的液滴(PDI测量范围为1～200 μm)，然后根据SMD的等效原理：假设一群液滴，其总表面积和体积与真实液雾的总表面积和体积相同，液滴数目可以不同，这群液滴的直径为SMD，得到算例1～5中喷雾场轴向位置9.5～10.5 mm处液滴的SMD。图6所示为算例2中使用PDI测量(图6(a))和对仿真结果进行处理(图6(b))这2种不同方法得到的粒径分布直方图，对比来看，两者在直径42 μm以上的部分有相似的分布，而对于较小粒径的液滴，由于受到Gerris数值方法中对于液滴捕捉及统计处理方法的影响，以及测量随机性和2种方法中统计数据来源不同的影响，其分布有较大的区别。但是由于在SMD的计算中，小液滴对于最终结果的影响要远远小于大液滴，所以认为数值模拟得到的液滴粒径分布与试验结果吻合较好。

图6 算例2试验与数值模拟粒径分布直方图对比

图7(a)、图7(b)分别为算例1～5中喷雾锥角和SMD的数值计算结果与试验结果的对比验证。结果表明，在不同压降条件下，喷雾锥角和液滴SMD的数值结果与试验结果吻合较好，其中喷雾锥角的最大相对误差为4.9%，SMD的最大相对误差为7.4%。因此认为Gerris数值方法可以对以上算例的雾化过程进行较为准确的数值模拟，这为后续基于数值模拟结果的讨论提供了支持。

图7 喷雾锥角和SMD的对比验证

2 数值模拟结果与分析

2.1 喷雾场宏观形态

在算例1～5中，不同的进口压力下，喷雾场会经历基本相同的扩张过程，由于压降不同导致的液膜初始速度不同，喷雾场的扩张速度也不同，但其整体喷雾场形态相似。算例6～9是在算例2的基础上加入了同轴旋转空气参与雾化，而同轴空气与液膜之间的相互作用导致喷雾场的形态发生了改变。取算例2和算例9作为典型算例来研究喷雾场随时间的变化过程，如图8所示，浅蓝色背景区域显示了喷雾场的俯视图和侧视图，深蓝色背景区域表示的是液膜的变化情况。从图像对比来看，在同一时刻，算例9喷雾场尺寸明显大于算例2，且算例9雾化效果明显较好。

图8 典型算例喷雾场随时间的变化

从侧视图来看，在算例2中，喷雾场在整个扩张过程中形态类似于扁平的漏斗状，而在算例9中，喷雾场初始形状为扁平漏斗状，之后从边缘处开始逐渐向内收缩，形成类似于碗状的轮廓。且相同时刻，算例9的喷雾场大小，特别是喷雾场的轴向长度明显大于算例2，说明同轴空气参与雾化能明显地加快喷雾场的扩张速度。从俯视图对比来看，除了喷雾场大小的区别外，算例9中液膜外缘散落的液滴明显多于算例2，在0.4 ms时，算例2基本上还是完整的液膜，而算例9中已经能观察到较多二次雾化产生的小液滴，说明同轴空气参与雾化能明显地加快喷雾场的雾化过程。从液膜变化情况来看，在0.2 ms时，两者内外层液膜均处于分开状态；而在0.4 ms之后，两者的内外层液膜均处于合并状态，说明2个算例均会经历双层液膜合并的过程。

在算例1～5中，由于液膜初始速度不同，因此不对同一时刻的喷雾场尺寸进行比较。而在算例2和算例6～9中，液膜初始速度相同，同轴旋转空气的轴向速度逐渐变大，对喷雾场尺寸造成了一定的影响，在0.8 ms时，各算例喷雾场的轴向长度和径向长度如图9所示。随着同轴旋转空气轴向速度的增大，在0.8 ms时的喷雾场轴向长度逐渐增大，但是这种增大趋势是逐渐变缓的，算例7的轴向长度比算例6增大了11.4%，而算例9的轴向长度相比于算例8仅增大了3.7%。在径向长度方面，由于同轴旋转空气与液膜相互作用使得喷雾场形状改变，雾锥向内收缩，算例6径向长度反而小于算例2，但是随着空气轴向速度增大，雾锥受到的空气作用逐渐增强，雾锥前缘在空气作用下的二次雾化过程加快，其形成的液滴群向各个方向运动，其中包括径向方向，导致喷雾场径向长度也逐渐增大。

图9 各算例0.8 ms时的喷雾场大小

在算例1～5中，副油路压降保持不变，主油路压降逐渐增大，因此，主油路液膜初始速度逐渐变大。表2列出了5个算例的喷雾场达到基本相同时喷雾场的尺寸和计算的实际物理时间。从数据可以看出，各个算例之间喷雾场的轴向长度和径向长度均相差很小，可以近似地认为喷雾场的大小相同，但相应的实际物理时间相差很大，为了便于比较，将这些时刻定义为控制时刻。随着压降的增加，控制时刻逐渐变小，说明喷雾场扩张速度随压降的增大逐渐变快。

表2 算例1～5喷雾场尺寸与对应的实际计算时间

图10(a)所示为算例1～5控制时刻的喷雾锥角，图10(b)所示的是算例2、算例6～9在0.8 ms时的喷雾锥角。从图10(a)来看，算例1和算例4、5喷雾锥角差别不大，算例2、3的喷雾锥角相比于其他3个算例则较小，喷雾锥角的变化与压降并没有表现出明显的规律，考虑到在一定的压降范围内，试验压降增大，喷雾锥角基本不变，综合仿真与试验结果，认为喷雾锥角的大小与压降的变化无关；而从图10(b)来看，同轴旋转空气参与雾化会明显地减小喷雾锥角，这点从图8中2个算例喷雾场的形态对比也可以得到验证，且同轴旋转空气轴向速度越大，喷雾锥角越小。

图10 各算例喷雾锥角

2.2 液膜破碎模式

图11(d)～图11(f)为算例2、7、9中液膜表面的破碎特征，观察发现3个算例液膜表面均存在明显的表面波动，均以狭缝形液膜穿孔为主，且存在部分不规则圆孔状液膜穿孔。因此3个算例的液膜破碎模式相同，均以波浪式破碎为主导，说明加入一定轴向速度范围内的同轴旋转空气，不会改变液膜的破碎模式。

对于同轴空气参与雾化的旋转锥形液膜，随着气液质量流率的增大，气液相互作用逐渐增强，基于气液相互作用程度的区别，液膜的破碎模式按照引起液膜破碎原因的不同可以分为3种：主导表面波发展导致的液膜破碎、R-T(Rayleigh-Taylor)与K-H(Kelvin-Helmholtz)不稳定性引起的液膜破碎和气动破碎。图11(g)～图11(k)为算例2和算例6～9共5个算例的完整液膜形态，对比发现随着同轴空气轴向速度增大，完整液膜的形态逐渐变得更规则，即周向上液膜破碎出现的位置更规律。观察完整液膜外部区域的液丝分布，发现随着同轴空气轴向速度增大其逐渐呈现明显的螺旋型分布，锥形液膜逆时针旋转的特征更为明显和规则。此时，锥形液膜被主导表面波占据，呈现出稳定的波动状态[14]，因此认为液膜的破碎是由主导表面波的发展导致的。

图11 各算例局部液膜破碎细节及液膜表面特征

2.3 双层液膜合并与表面波动

图12为各算例双层液膜的扩张过程，随着时间的推移，液膜逐渐扩张，内、外2层液膜在扩张过程中逐渐合并成单层液膜，合并后的液膜继续扩张直到完成液膜的一次破碎。在算例1中，双层液膜在0.1 ms之前就已经合并在一起，在放大图中可以观察到由于液膜合并产生的明显的表面波动；而其他算例在0.1 ms时双层液膜未接触，液膜表面光滑。在算例3、5、7、9中，双层液膜开始接触的时间在0.3～0.4 ms，对比图12中红框的放大图发现，算例7、9中双层液膜处于即将要接触的状态，在算例3中双层液膜之间还有一段距离，而在算例5中，双层液膜之间的距离则比较远。同时，由于算例5压降最大，算例3次之，这2个算例中液膜扩张速度也更快，但是其液膜相互接触的时间反而落后于其他算例。综合所有工况条件及结果分析认为：压降的增大会推迟双层液膜接触与合并的时间，而同轴旋转空气参与雾化对双层液膜的合并时间没有影响。

图13(a)～图13(f)为算例2中双层液膜合并过程及双层液膜接触位置细节特征，在0.3 ms时，双层液膜有合并的趋势，但还没有接触，此时，外层液膜表面比较光滑，没有明显的波动(见图13(a)中I及图13(d))。在0.4 ms时，双层液膜处于合并过程，内层液膜向外扩张接触到外层液膜，双层液膜合并成较厚的单层液膜，在外层液膜和内层液膜接触的表面产生剧烈的波动，而液膜外侧则没有观察到明显的波动(见图13(b)中II及图13(e))。在0.5 ms时，双层液膜已经完全合并，表面波在合并后的液膜表面传播并增大，最终导致液膜破碎(见图13(c)中III及图13(f))，同时，在整个合并过程中，液膜的喷雾锥角由合并前的107.7°增加到合并后的113.5°。

Li和Tankin[24]、Ibrahim[25]的研究表明小韦伯数We下液膜由曲张模式表面波主导，大We下由正弦模式表面波主导。观察图12中算例1(外层液膜We为1 360)放大图发现，液膜表面波正弦模式和曲张模式并存，且能观察到明显曲张模式时的液膜形态。由图13(c)可知，t=0.5 ms时算例2(外层液膜We为3 197)III处液膜表面波动则为正弦模式占主导，但是仍能观察到曲张模式对液膜表面产生的影响(图13(f)中IV处)。随着压降增大，液膜初始速度增大，We增大，图13(g)～图13(i)算例3、4、5结果显示，液膜表面波主要为正弦模式表面波，基本观察不到曲张模式表面波。在算例2基础上加入同轴旋转空气之后，在算例6～9中，随着旋转空气速度的增大，从图11(g)～图11(k)中观察到液膜逆时针旋转的特征逐渐变得更为明显，且液膜表面呈现出规则的逆时针旋转的螺旋状波动。参考文献[26-27]关于环形液膜在旋转气流中主导表面波模式变化的研究结果，认为在同轴旋转空气的影响下，锥形液膜表面波动在算例2的轴正弦模式为主导中加入了螺旋模式，且随着空气旋转速度的增大，螺旋模式占据的比重逐渐增大。

图12 各算例双层液膜扩张过程

图13 各算例中液膜合并前后表面波动特征

2.4 液膜破碎长度

液膜破碎长度是使用MATLAB对喷雾场俯视图的像素值进行处理获得的。首先，检索图像内各像素的RGB(Red Green Blue)，以初始液膜环的圆心作为中心，依次向外搜索距离中心位置厚度为3个像素的环形图。之后，统计每个环形图中每个像素的Red值，当一个像素的Red值超过127时，认为该像素被液体占据，否则就认为是被空气所占据，最后计算每个环形图中液体所占比例。由于液体体积分数随着距喷嘴出口的距离而变化，文献[7]研究发现，液体所占比例为80%时的位置是液体含量急剧减小的初始位置，该位置处液膜刚开始断裂，因此取液体体积分数为80%处距喷嘴出口的距离为液膜破碎长度。基于文献[7]和以上所述MATLAB处理方法，取液体占比为80%时环形图的位置与中心位置的距离作为破碎半径，依据图14所示方法，获得液膜破碎长度。

图14 液膜破碎长度获取方法

使用以上方法获取算例1～5控制时刻的破碎长度和算例2、算例6～9在0.8 ms时的破碎长度，得到的数据绘制的点线图如图15所示。算例4中破碎长度的突然变大是因为算例4中压降较大，双层液膜的合并推迟，在控制时刻(算例4的控制时刻为0.49 ms)时双层液膜刚开始合并，由于双层液膜合并引起的表面波动还没有增长到足够大，因此破碎长度较大，而算例5中液膜初始速度更大，扩张速度更快，在控制时刻，双层液膜合并引起的波动已经增长了足够久，导致其破碎长度较小。排除算例4的影响后，由图15得到以下结论：随着压降或液膜初始速度、We增大，液膜破碎长度逐渐减小；同轴旋转空气参与雾化会减小液膜的破碎长度，随着同轴空气轴向速度的增加，液膜破碎长度减小，但是减小幅度较小。

图15 各算例液膜破碎长度

3 结 论

采用数值模拟的方法对不同压降条件下的双路离心式喷嘴外流场雾化过程进行了数值模拟，引入同轴旋转空气参与雾化来模拟其对液膜一次破碎的影响。重点研究了不同工况下的喷雾场宏观形态、液膜破碎特征、双层液膜的合并及破碎长度。同时还研究了双层液膜合并对喷雾锥角的影响以及不同工况下液膜的破碎模式和表面波动模式。研究的主要结论归纳如下：

1)同轴旋转空气参与雾化之后，喷雾场的形状从扁平的漏斗状变为碗状，压降越大，喷雾场扩张速度越快，同轴旋转空气速度越大，同时刻喷雾场整体尺寸越大，且喷雾场末端收缩幅度也越大，导致喷雾锥角越小。

2)从液膜的破碎特征来看，压降的增大会使液膜的破碎模式由波浪式破碎为主导逐渐变为由穿孔膜破碎为主导，且加入同轴空气不会改变液膜的破碎模式；从液膜的破碎原因来看，各算例液膜破碎均由主导表面波的发展导致，而在主导表面波的发展中，压降的增大会使液膜的表面波动由曲张模式与正弦模式共存逐渐变为由正弦模式为主导，同轴空气参与雾化则会在液膜主导表面波模式中引入螺旋模式。

3)压降的增大会推迟双层液膜接触与合并的时间，而同轴旋转空气参与雾化对双层液膜的合并时间没有影响，双层液膜的合并会在液膜表面产生剧烈的表面波动，同时会略微增大液膜的喷雾锥角。

4)在喷雾场扩张到一定程度后，液膜的破碎长度会随着压降的增大而减小，同轴旋转空气参与雾化也会减小液膜破碎长度，但是减小幅度略小。